Тренировочные варианты- бесплатно на сайте ЕГЭ? ОК!
 На этой странице представлены тренировочные варианты для подготовки к ЕГЭ по математике — 2019.
На этой странице представлены тренировочные варианты для подготовки к ЕГЭ по математике — 2019.
Задачи из первой части, в отличие от стандартных вариантов для подготовки к ЕГЭ по математике, содержат «изюминку», требуют внимательного чтения условия и хорошего знания теории. Они адресованы ученикам, которые хотят получить высокий балл на ЕГЭ.
Каждый вариант сопровождается видео решениями самых сложных задач варианта. Если вы хотите получать на почту видео решения второй части тренировочных вариантов, подпишитесь на рассылку сайта.
Вопросы по заданиям из первой части вариантов можно задавать в комментариях.
Видео решения заданий 13-18 из второй части вы можете найти на моем канале на youtube
Тренируйтесь, и сдавайте ЕГЭ на максимальный балл!
Отличный способ подготовиться к ЕГЭ — это
Для учителей и репетиторов! Вы можете купить презентации к видео решениям заданий 13-18 + ссылки на видео решения. Это превосходная возможность подготовить учеников на высокий балл, сэкономив свое время и силы.
тренировочные варианты №№ 1-10 тренировочные варианты №№ 11-201. Тренировочный вариант №1
2. Тренировочный вариант №2
3. Тренировочный вариант №3
4. Тренировочный вариант №4
5. Тренировочный вариант №5
6.Тренировочный вариант №6
7. Тренировочный вариант №7
8. Тренировочный вариант №8
9. Тренировочный вариант №9
10. Тренировочный вариант №10
11. Тренировочный вариант №11
12. Тренировочный вариант №12
13. Тренировочный вариант №13
14. Тренировочный вариант №14
15. Тренировочный вариант №15
16. Тренировочный вариант №16
17. Тренировочный вариант №17
18. Тренировочный вариант №18
19. Тренировочный вариант №19
20. Тренировочный вариант №20
21. Тренировочный вариант №21
22. Тренировочный вариант №22
23. Тренировочный вариант №23
24. Тренировочный вариант №24
25. Тренировочный вариант №25
26. Тренировочный вариант №26
27. Тренировочный вариант №27
28. Тренировочный вариант №28
29. Тренировочный вариант №29
ege-ok.ru
Репетитор по математике — онлайн
Меня зовут Инна Владимировна Фельдман. Я профессиональный репетитор по математике. Я готовлю к ОГЭ и ЕГЭ, к вступительным экзаменам в специализированные школы, занимаюсь со школьниками, которые хотят улучшить свои знания по алгебре и геометрии.
В 1983 году я окончила МГУ им. Ломоносова, факультет Вычислительной математики и кибернетики. С тех пор я преподаю математику.
Мои ученики успешно сдавали экзамены в престижные ВУЗы Москвы: РЭА им. Плеханова, МГИМО, МИФИ, ВШЭ, МГУ им. Ломоносова, ГУУ и другие.
По второму образованию я психолог, поэтому мне легко удается понять, какие качества мешают школьнику научиться решать задачи по математике. Это может быть невнимательность, или боязнь получить неправильный ответ, или нежелание признавать свои ошибки, или привычка действовать по шаблону, или неумение проверить себя в процессе решения задачи.
На наших занятиях мы не только учимся решать задачи, развиваем логику и математическое мышление. Мы учимся справляться со страхом неудачи, не опускать руки перед трудностями, осознавать качества, которые мешают учиться, начинать все с нуля, активизировать знания и искать решение в ситуации, когда не знаешь с чего начать.
Математика как наука представляет собой стройную, логичную, непротиворечивую теорию. Я очень радуюсь, если мне удается раскрыть ученикам взаимосвязи, показать, как из одного факта вытекает другой, как они складываются в общую картину. И не имеет значения уровень подготовленности ученика — картина может обрастать частностями, подробностями (теоремами и алгоритмами) — но суть ее от этого не меняется. Умение за частностями увидеть общую закономерность, а, поняв закономерность, не забыть про частности — трудно переоценить и в обычной жизни. Оно прекрасно развивается именно при решении математических задач, и наилучшим образом способствует их решению. На своих уроках я помогаю своим ученикам развивать это умение.
Я с большим уважением отношусь к тому, что другой человек может совершенно не понимать элементарные, с моей точки зрения, вещи.
Мой опыт показывает, что детям, как правило, начинает нравиться математика, если они её понимают, если у них получается решать задачи. У каждого ребёнка есть свой «потолок», свой уровень компетентности. И важно, чтобы обучение происходило именно на границе компетентности данного конкретного ребёнка: «я могу решить эту задачу — я крут!». Выход в область некомпетентности часто влечёт за собой потерю интереса к предмету: «я всё равно ничего не понимаю». Занижение «потолка», решение слишком простых для данного ребёнка задач вызывает скуку и, как следствие, потерю интереса. Поэтому на своих занятиях я стараюсь найти баланс между стремлением достичь определённой цели (сдать ЕГЭ на нужный балл, подтянуть предмет, поступить в престижную школу) и тем, что в реальности можно требовать от конкретного ребёнка.
Часто родители приводят детей, которые хотят получить высокий балл на ЕГЭ. Но уже после первого занятия выясняется, что у ребёнка отсутствуют базовые навыки. К сожалению, я не экстрасенс и не могу научить за несколько занятий тому, на что в школе уходит несколько лет. Я не могу ввести все необходимые знания «внутривенно» — их надо «переварить» и ассимилировать. К сожалению, родители, которые внезапно незадолго до ЕГЭ заметили, что у ребёнка хромает математика, и настроены на быстрый результат, бывают разочарованы, когда видят, что обучение продвигается не с той скоростью, как им хотелось бы.
Ещё раз могу заверить, что мы (именно МЫ) двигаемся с максимальной скоростью, на которую способен ученик.
Я не «натаскиваю» на решение определённых задач: я объясняю основные принципы решения, достаточно универсальные для целого класса задач. Этот подход, наряду с требованием знания необходимой теории, наиболее продуктивен и даёт хороший результат.
Мои ученики занимаются с удовольствием: очень быстро у нас устанавливаются тёплые, доверительные отношения. Однако это не сказывается на строгости в отношении выполнения домашних заданий и знания теории.
Репетитор по математике — онлайн
В последнее время я начала проводить уроки математики по SKYPE. В отличие от большинства коллег я не использую во время занятий виртуальную доску и графический планшет. Мы пользуемся USB веб-камерой, которая направлена на тетрадку. Я вижу, что пишет ученик, ученик видит, что пишу я. И, разумеется, мы слышим друг друга. Поэтому дистанционные занятия по SKYPE практически не отличаются от очных и даже обладают рядом преимуществ. Единственное требование — хорошее качество связи.
Вот некоторые отзывы моих учеников (скриншоты с сайта «Ваш Репетитор»)
показать
Другие отзывы моих учеников можно прочитать здесь. Чтобы понять, как я работаю, посмотрите видеоматериалы на этом сайте.
Я живу и работаю в Москве. Стоимость занятий: 2500 руб за 45 минут.
Если Вам нужен репетитор по математике для индивидуальных занятий, напишите мне, и я обязательно вам отвечу. Как правило, сетка занятий заполняется уже к концу сентября нового учебного года, поэтому лучше записываться заранее.
Репетитор по математике — роскошь или необходимость?
Все любящие родители стремятся дать своим детям хорошее образование. Желательно высшее. Для поступления в большинство ВУЗов необходимо сдать экзамен по математике. И если у ребенка не складываются отношения с этим предметом, встает вопрос о том, чтобы обратиться за помощью к репетитору по математике.
Как не пропустить тот момент, когда «еще рано» превращается в «уже поздно»? показать
Изучение школьного курса математики на базовом уровне не требует особых математических способностей. Его цель — приобретение вычислительных навыков и навыков алгебраических преобразований. Ученик должен освоить определенные алгоритмы и научиться их применять при решении уравнений и неравенств, научиться выполнять действия с геометрическими фигурами, используя теоремы и формулы геометрии. А также научиться использовать полученные знания при решении прикладных задач.
Казалось бы все просто. Однако трудности начинаются с первых шагов. Дело в том, что курс математики выстроен таким образом, что неосвоенное простейшее действие не дает возможности освоить более сложные. Например, если ребенок не научился складывать числа с разными знаками, то все арифметические действия, в которых встречается эта операция, он будет выполнять с ошибками. И никакой калькулятор ему не поможет. Если ребенок не научился приводить дроби к общему знаменателю, то вряд ли он осилит алгебраические преобразования. Примеров такого рода можно приводить множество. Дело в том, что крошечный пробел в знаниях со временем, как снежный ком, обрастает глобальным непониманием объяснения нового материала на уроке: «откуда они это взяли?», «как это получилось?». А если нет понимания, то старательные дети (чаще девочки) зубрят с неочевидным результатом, а менее старательные (чаще мальчики) «забивают» на математику до тех пор, пока не «клюнет жареный петух».
В этой ситуации помощь опытного репетитора по математике очевидна: поскольку репетитор знает, какой набор умений и навыков необходим для выполнения каждого математического действия, он легко диагностирует «слепые пятна» и затем их ликвидирует. Причем чем раньше это произойдет, тем лучше будет чувствовать себя ребенок на уроках, и тем меньше денег придется вкладывать родителям в его образование в дальнейшем.
Следующим этапом, вызывающим серьезные трудности, является развитие умения использовать алгоритм (то есть известную последовательность действий) при решении определенного класса задач. И наибольшую трудность здесь вызывает не столько само использование алгоритма, сколько распознавание того, что данная задача принадлежит данному классу. Многие школьники настолько привыкают действовать по шаблону, то есть выучиваются решать конкретный вид задач, что малейшее отклонение условия задачи от привычного вызывает ступор и панику.
Репетитор по математике объясняет не только алгоритмы решения конкретного класса задач, но и учит распознавать, какому классу принадлежит данная задача. Учит структурировать информацию и извлекать нужную. То есть как «собрать глаза в кучку», если в голове туман и мысли разбегаются.
Очень тяжело дается многим школьникам решение задач по геометрии. И дело здесь не столько в незнании теорем и формул (я беру редкий случай, когда ученик знает все необходимые теоремы и формулы), сколько в том, что очень многим трудно выстроить последовательную логическую цепочку рассуждений. Трудно выделить из текста задачи то, что дано, то есть использовать в решении все заданные параметры и не добавлять от себя («видно из чертежа») то, чего нет в условии. Трудно, одновременно держа в голове то, что дано, и то, что нужно найти, перекинуть мостик от одного к другому.
В этом случае репетитор по математике обучает необходимым действиям, которые значительно облегчают этот процесс и дают возможность школьникам, не имеющим понятия с какой стороны подступиться к геометрическим задачам, научиться их решать на уровне первой части ГИА или ЕГЭ по математике.
Еще один важный момент. Преподавание в общеобразовательной школе ориентировано на среднего ученика: на средний темп усвоения материала, на среднюю скорость решения задач. Но мы все с вами знаем, что такое «средняя температура по больнице». Даже если учитель математики старается организовать максимально индивидуальный подход, он физически не в состоянии объяснить каждому из 30 учеников в классе то, что ему не понятно, и при этом дать и проверить более сложные задачи тем, кто уже все понял. К тому же очень многие дети стесняются задавать вопросы на уроке, особенно, если учитель их к этому не поощряет, тушуются в ситуации сравнения с другими. Сильные же дети, которые легко осваивают математику, часто остаются вовсе без присмотра. Таким образом, многие из тех, кто отклоняется от среднего в ту или иную сторону, выпадают из образовательного процесса. И если для сильных учеников есть профильные классы, то тем, кто немного «тормозит» бывает очень непросто.
И в этом случае помощь репетитора по математике также необходима: он возвращает ребенку уверенность в своих силах, объясняет материал в комфортном для него темпе, дает возможность подумать над решением задачи столько времени, сколько ему нужно. Последнее очень важно, поскольку для изучения математики, возможно более, чем для чего-либо другого справедливо изречение Конфуция: «Я услышал и забыл. Я увидел и запомнил. Я сделал и понял.» Чтобы понять, нужно обязательно сделать самостоятельно, недостаточно списать готовое решение с доски. Репетитор по математике будет требовать от ребенка максимум того, на что он способен, но не более. «Выше головы не прыгнешь», говорит русская пословица. «У человека есть свой потолок», писал Бродский. Опытный репетитор по математике работает в зоне ближайшего развития ребенка, постепенно поднимая его «потолок», стимулируя к развитию.
Отдельная тема — это подготовка к ОГЭ и ЕГЭ. Ни для кого не секрет, что во многих школах часть С вообще не рассматривают. Поэтому для подготовки к экзаменам на хорошем уровне требуются дополнительные занятия. Что выбрать: курсы или индивидуальные занятия? Ответ на этот вопрос содержится в предыдущем абзаце.
И, возможно, самое главное. Цель гораздо легче достигнуть, если процесс ее достижения доставляет удовольствие. Если ребенок ходит на занятие с репетитором с удовольствием, то и результаты будут гораздо выше. Хороший репетитор по математике может организовать процесс изучения математики именно таким образом.
Так что если вы решили, что вашему ребенку нужна помощь репетитора по математике, обращайтесь:)
Репетитор по математике: мой подход к урокам
Дао математики
Много лет я преподаю математику. Казалось бы — десятки лет одно и то же: одни и те же формулы, практически одни и те же задачи, одни и те же вопросы…Недалеко и до профессионального выгорания, когда появляются скука и раздражение, перестаешь получать удовольствие от работы, начинаешь воспринимать уроки как тяжелую повинность… Многим знакомы эти чувства. Не скрою, они и мне тоже знакомы. К счастью, они начинают появляться ровно перед летними каникулами, и не успевают сказаться на моих учениках.
Мой интерес к преподаванию математики не ослабевает с годами по той простой причине, что я рассматриваю изучение математики не только как единственную конечную цель своих уроков, но и как средство, как Путь…Средство саморазвития, Путь к себе.
Я уверена, что на уроках математики можно научиться многому.
1. Репетитор по математике: осознанность
показать
«Секрет так называемых умных людей состоит в осознанности. Ясность ума определяется степенью осознанности. Одни люди ясно мыслят и ясно излагают, у других путаница в голове. Острый ум, с одной стороны, и тупость, с другой — это вовсе не степени развития интеллекта, а разные степени осознанности. Тупость — это скорее психологическая защита от нежеланной информации: «Ничего я не хочу знать, отстаньте вы от меня!». Острый ум — это, наоборот, открытость, любознательность, желание получать и обрабатывать информацию: «Хочу всё знать!». Страх и ярость — это крайние проявления неосознанности» — Зеланд В.
«Никакое влияние на человека не может быть более навязчивым и предопределяющим, чем то, которое он не осознает.» — Кернбер О.
«Будьте внимательны к своим мыслям, они — начало поступков» — Лао-Цзы
Изучение математики в большей степени, чем любой другой дисциплины, способствует развитию осознанности. В это слово я вкладываю умение в каждый момент времени ответить на вопросы «что я сейчас делаю?» и «о чем я сейчас думаю?».
К сожалению, обучение в общеобразовательной школе, за редким исключением, основано на двух принципах: «делай как я» и «выучи формулу и подставь в задачу». Дети, которые задают много вопросов раздражают, так как отвлекают и мешают вести урок: нужно проходить программу, нет времени, чтобы остановиться и подумать, разобрать разные подходы, вернуться к пройденному. Решение большого числа однотипных задач дает хороший, но — увы — кратковременный результат на ближайшей контрольной работе. Такова обратная сторона обучения в общеобразовательной школе: развитие личности — это всегда штучный товар, а массовая школа, за редким, повторю, исключением, это огромный конвейер, образовательная машина, подгоняющая все живое под образовательный стандарт.
Недавно начала заниматься с новой ученицей. Старательная девочка, имеющая пятерку за итоговую контрольную в 10 классе, путает высоту треугольника с серединным перпендикуляром, уверена, что любые две хорды пересекаются в центре окружности, и даже когда правильно решает задачу не может объяснить, как она получила ответ. На просьбу обосновать свое решение, следует классический ответ: «вы так сказали». Конечно, я так сказала. Но перед этим я долго, разными способами этот ответ обосновывала.
Когда нет понимания, вся полученная информация представляется набором не связанных между собой фактов, и тогда решение задачи сводится мучительному вспоминанию аналогичной.
Если не закладывать, не удобрять и не поливать умение критически осмысливать информацию, на его месте прорастает навык послушно заглатывать то, что вкладывают в мозги родители, учителя и другие заинтересованные лица. И тогда даже не возникает желание задать себе, например, такие вопросы: «откуда взялось это правило?», «как оно связано с тем, что мне уже известно?»
В этом отношении особенно прекрасно решение задач по геометрии. Геометрия учит после любого утверждения ставить запятую и говорить «потому что, …». Никакое утверждение не принимается на веру, а должно быть обосновано с помощью неоспоримых фактов, которые вытекают из того, что дано в условии и что уже доказано. Отличный жизненный навык!
В последнее время моими любимыми вопросами на занятиях стали такие: «что ты сейчас делаешь?», «с какой целью ты это делаешь?», «откуда это следует?», «как ты можешь себя проверить?» И именно на них труднее всего получить вразумительный ответ.
Неумение описать свои действия словами (например, «сейчас я ищу дискриминант») говорит о «каше» в голове, нечеткости мышления — это то, над чем в первую очередь нужно работать.
Решая осознанно математическую задачу ребенок учится спрашивать себя: что мне дано? что из этого следует? чем эта задача похожа на те, которые я уже решал? чем отличается? что я могу сделать в первую очередь? к чему это приведет? какие теоремы я могу использовать?
Не эти ли вопросы нужно задавать себе, решая задачи, которые ставит перед нами Жизнь.
2. Репетитор по математике: внутренняя честность
Внутренняя честность — это сестра-близнец осознанности. Это умение видеть ситуацию и себя в ней так, как есть. Довольно легко научить ребенка не обманывать других, но чрезвычайно трудно научиться не обманывать себя. Потому что ребенок всегда стремится соответствовать ожиданиям взрослых, и очень расстраивается, если это не удается сделать. И поэтому старается не замечать в себе то, что, по его мнению не соответствует ожиданиям близких.
К сожалению, большинство взрослых тоже не умеют относиться к себе честно: мы либо гнобим себя за малейший промах, либо игнорируем его. Внутренняя честность — это осознавание своих качеств: как тех, которые общество традиционно оценивает со знаком «+», так и «негативных», и принятие их. (Я специально взяла в кавычки, потому что любое качество всегда имеет обратную сторону.) Принятие вовсе не означает желание на все наплевать и оставить как есть — принятие означает признание, констатацию факта, за которыми следует решение, что с этим делать.
В математике классический пример игнорирования проблем — так называемые «ошибки по невнимательности», причинами которых при ближайшем рассмотрении оказываются незнание правил, неумение читать условие, незнание таблицы умножения, и многое другое. Но ребенку ведь гораздо приятнее считать, что это невнимательность. Типа умный, но невнимательный. И он с удовольствием воспринимает именно первую часть этой фразы, не предпринимая никаких усилий для улучшения ситуации.
Повторю: можно решить «проблему» только если признать ее наличие. Например, если я знаю про себя, что медленно соображаю, что мне нужно больше времени, чем другим, чтобы понять какую-то тему, то я просто дам себе больше времени. Если я знаю про себя, что страшно невнимательна, то десять раз прочитаю условие и десять раз проверю свое решение. Если я признаю, что я неорганизованный человек, то установлю на телефон напоминалку, составлю расписание и постараюсь ему следовать. Когда я признаю в себе какое-то качество, оно теряет силу и становится управляемым.
В этом деле самое главное, чему нужно научиться, и чему научиться чрезвычайно трудно — не сравнивать себя с другими. Недовольство собой — отличный стимул. Оно не позволяет расслабиться и остановиться на достигнутом, заставляет ставить новые цели и достигать новых вершин. Развиваться, расти, двигаться вперед, преодолевать — но точкой отсчета всегда должен быть сам человек. Поскольку сравнение себя с другими порождает либо манию величия, либо комплекс неполноценности. Уж это я знаю по себе!
Мы все уникальны. Сравнивая себя с другими, мы всегда вырываем из контекста, сравниваем несравнимое, типа «крокодил более длинный, чем зеленый»
«Путь мудреца — действовать, но не соревноваться» — Лао-цзы
Итак, уроки математики — отличный тренажер для развития внутренней честности: причины ошибок легко диагностируются, продвижение или, наоборот, буксование, легко фиксируются. Все достаточно объективно и прозрачно. И главное, ученик сам может отметить места, где были допущены ошибки и проговорить их причину. Он может оценить свои успехи и исследовать причины неудач.
3. Репетитор по математике: принятие своих особенностей
«Торопитесь медленно и прибудете скоро» — Миларепа
Часто родители моих учеников жалуются, что ребенок неплохо работает на уроке, но как дело доходит до контрольной или самостоятельной — сплошные двойки. Не успевает…
Да, для многих детей самостоятельная или контрольная — это стресс. А если еще и ограничено время, то стресс вдвойне.
Дело в том, что на контрольной или самостоятельной не проверяется умение думать — только наработанные навыки. Однако разным людям требуется разное время для того, чтобы умение переросло в навык. Например, у меня очень плохая координация движений. Когда я училась водить машину, я очень долго училась переключать передачу: одновременно отжать сцепление и переключить передачу! — невозможное действие. Я тогда говорила себе: я буду долго учиться, но я научусь. Потом еще 10 лет я не могла слушать музыку в салоне — она меня отвлекала. Но вот прошло всего 15 лет, и я вожу машину «на автопилоте», совершенно не вникая в процесс.
Разумеется, у школьников нет пятнадцати лет на то, чтобы, например, научиться раскладывать многочлен на множители. Но если сразу не получается, нужно знать про себя, что этому процессу нужно уделить больше времени, чем другому ученику, чтобы получить хорошую оценку на проверочной работе.
А встречаются торопыги — решают так, как будто за ними кто-то гонится. И конечно, лепят по ходу кучу ошибок. Таким нужно притормаживать себя, учиться глубже дышать и расслабляться. А для этого сначала обращать внимание на свое состояние. Не корить себя за это, а просто знать про себя.
Этот принцип действует в отношении других качеств, которые «мешают» учиться — если посмотреть на них под другим углом зрения и приручить.
4. Репетитор по математике: учимся на ошибках
«Из исправления ошибок обязательно родится мудрость» — Хуэйнэн
Что делают родители и учителя, когда ребенок ошибается? Правильно, ругают. Поэтому все, и взрослые, и дети, ужасно боятся ошибиться. Уже после того, как ошибка сделана, и отрицательный опыт получен, мы сожалеем о содеянном и говорим: «Эх, зря я тогда… надо было…» И всегда забываем о том, что тот, кто сделал ошибку, и тот, кто о ней сожалеет — два разных человека. Это «я» до получения опыта и «я» после его приобретения. Но чтобы приобрести опыт, надо было эту ошибку совершить.
На наших занятиях, если ученик примерно представляет как решать задачу, я редко вмешиваюсь в ход решения. И даже если вижу, что он ошибается, редко поправляю: ученик должен получить неправильный ответ, объяснить свои действия, постараться найти место, где ошибся, указать причину ошибки, и что намерен делать, чтобы больше такую ошибку не повторять.
Есть пословица: «мудрый человек учится на чужих ошибках, умный — на своих, дурак не учится вообще». Я бы перефразировала ее так: «мудрый человек не делает ошибок, умный учится на своих ошибках, дурак не учится вообще». Невозможно научиться на чужих ошибках, потому что обучение стимулирует развитие только в том случае, если представляет собой не просто «регистрацию внешней информации» (Ж. Пиаже), но «переваривание» и усвоение информации посредством собственного опыта. Обучение есть получение информации, использование ее в своих действиях с последующим их осознаванием.
Решение задач — отличный способ научиться действовать и не бояться ошибиться. Это абсолютно безопасная ситуация для формирования умения сконцентрироваться и сделать первый шаг в ситуации неопределенности. Я обычно говорю: «Сделай хоть что-нибудь, и посмотри, что получится. Следующий шаг станет виден после того, как сделаешь предыдущий».
«Сделайте первый шаг. Смелое преодоление одного маленького страха дает вам мужество, чтобы сделать второй» — Дайсаку Икеда
Ведь поняв, что двигаешься в неверном направлении всегда можно вернуться на исходные позиции и начать все с начала. (И не только при решении задач по математике!)
5. Репетитор по математике: выбор и намерение
«Вы можете получить помощь от учителя, но вам придётся многому научиться самим, сидя в одиночестве в комнате» — Доктор Сьюз
«Учителя только открывают двери, дальше вы идете сами» — Китайская пословица
В основе всех наших действий лежит выбор. Если выбор не сделан, если цель не определена или если нет намерения ее достичь, то все усилия по достижению этой цели оказываются имитацией бурной деятельности и не дают желаемых результатов. Чтобы получить хороший результат, ученик должен сам четко представлять, зачем он ходит на занятия. Это может быть высокий балл на ЕГЭ или ГИА, хорошие оценки. (К сожалению, редко можно услышать такой ответ: «хочу лучше понимать математику и научиться решать задачи». Обычно к репетитору по математике обращаются чтобы исправить ситуацию с оценками — именно они основной критерий истинного положения вещей. Однако, как я уже писала, весьма ненадежный). Если решение улучшить ситуацию по математике — это осознанное решение самого ребенка, а не родителей, то результат обязательно будет.
В ситуации выбора ученик оказывается всегда, например оставшись наедине с домашним заданием. Я обычно не проверяю напрямую его выполнение (хотя, по тому, как усвоен материал, я всегда вижу, было ли оно сделано.) Как правило, если цель домашнего задания — отработка пройденного материала, ученик всегда получает на дом задачи с ответами, он может проверить правильность ответа, а во многих случай и правильность решения, и ВСЕГДА может задать на следующем занятии вопрос, если что-то непонятно. Дома продолжается работа, начатая на занятии. Я знаю по себе, что самостоятельный разбор готового решения полезен не менее, чем самостоятельное решение задачи. Однако, если ребенку все равно, если он не настроен на результат, он будет по школьной привычке «откашивать» от домашней работы. Но это его выбор. И тогда, к сожалению, продвижение минимально.
Но если есть намерение и усердие, то результаты обычно не заставляют себя долго ждать. И не только с точки зрения прогресса в изучении математики:
ege-ok.ru
18 Задание (2015) (C6) – Репетитор по математике
Задание 18 из реального ЕГЭ по математике 01.06.2018.
Найти все значения , при каждом из которых система уравнений
Имеет ровно четыре различных решения.
Будем решать задачу графически.
Первое уравнение: произведение двух множителей равно нулю, если хотя бы один из них равен нулю.
То есть первое уравнение равносильно совокупности:
Нам удобно выразить через :
Или так:
В итоге получаем систему:
График первого уравнения совокупности представляет собой семейство прямых с переменным коэффициентом наклона, которые проходят через точку с координатами .
График второго уравнения совокупности представляет собой семейство прямых с переменным коэффициентом наклона, которые проходят через точку с координатами .
График третьего уравнения представляет собой окружность с центром в начале координат, радиус которой равен 4.
Система имеет ровно четыре решения, если каждая прямая совокупности имеет с окружностью две общие точки.
Изобразим графики всех уравнений на координатной плоскости. Так как мы решили выразить через , вертикальная ось будет ось , а горизонтальная — ось .
Рассмотрим семейство прямых . (1)
Прямые семейства имеют две точки пересечения с окружностью, если расположены в голубой области. Эта область ограничена касательными к окружности, проведенными из точки .
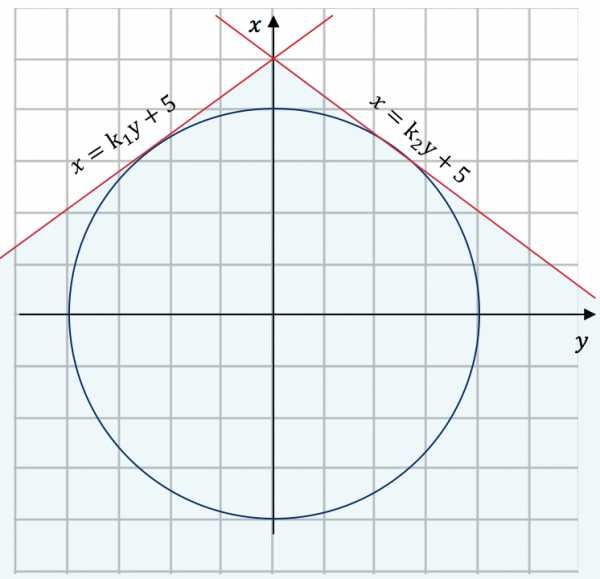
То есть если коэффициент наклона должен быть больше чем или меньше чем :
или .
Найдем и .
Из соображения симметрии ясно, что .
Рассмотрим прямоугольный треугольник . — радиус, проведенный к точке касания.
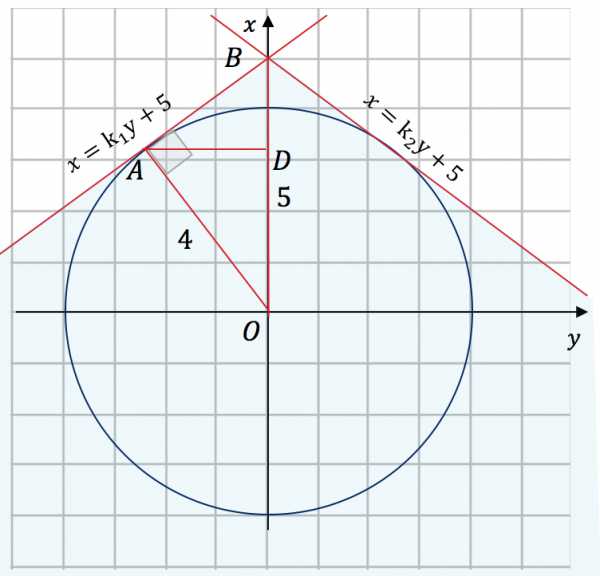
, отсюда
Следовательно, ; .
Отсюда или .
или (3)
Рассмотрим семейство прямых . (2)
Прямые семейства имеют две точки пересечения с окружностью, если расположены в зеленой области. Эта область ограничена касательными к окружности, проведенными из точки .
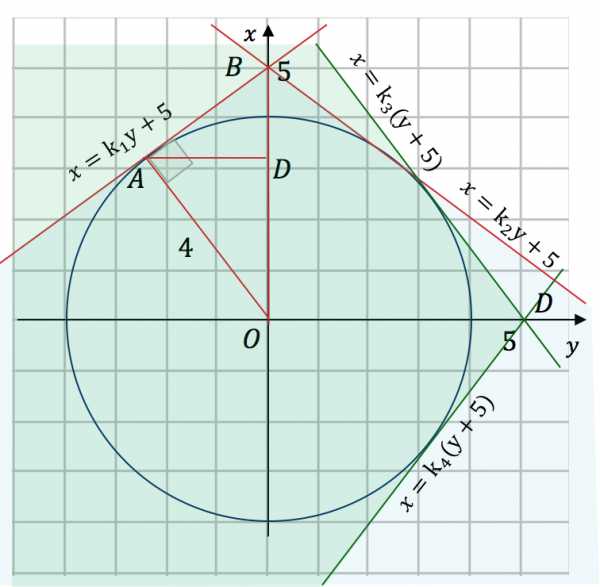
То есть коэффициент наклона прямых должен быть больше чем или меньше чем :
или .
Чтобы найти и рассмотрим прямоугольный треугольник . — радиус, проведенный к точке касания.

Отсюда ; .
Тогда .
Следовательно, или .
Отсюда получаем: или . (4)
Кроме того, важно заметить, что семейства прямых (1) и (2) имеют общую прямую, которая проходит через точки и . Уравнение этой прямой :
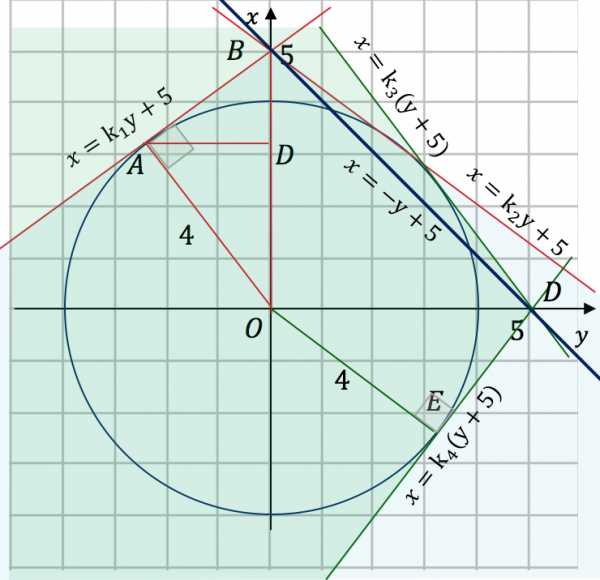
Значит, если коэффициент наклона равен -1, то система имеет два решения, и этот случай нам не подходит. Отсюда:
. (5)
Подытожим:
Ответ: UU
ege-ok.ru
14 Задание (2016) (C2) – Репетитор по математике
14 Задание (2016) (C2)Диагностические работыСТЕРЕОМЕТРИЯ
Задание 14 из тренировочной работы 06.03.2018
На окружности основания конуса с вершиной отмечены точки , и так, что . Медиана треугольника пересекает высоту конуса.
а) Точка — середина отрезка . Докажите, что угол прямой.
б) Найдите угол между прямыми и , если .
Решение. показать

а) Пусть — точка пересечения медианы с высотой конуса. Точка принадлежит плоскости треугольника , следовательно, высота конуса также принадлежит плоскости треугольника .
Высота конуса является высотой треугольника . Треугольник равнобедренный, следовательно, высота является медианой, и основание высоты, точка , является серединой отрезка . Следовательно, точка — центр окружности основания конуса и — диаметр основания конуса.
Далее. По условию , следовательно, треугольник — равнобедренный, медиана является высотой, и отсюда :
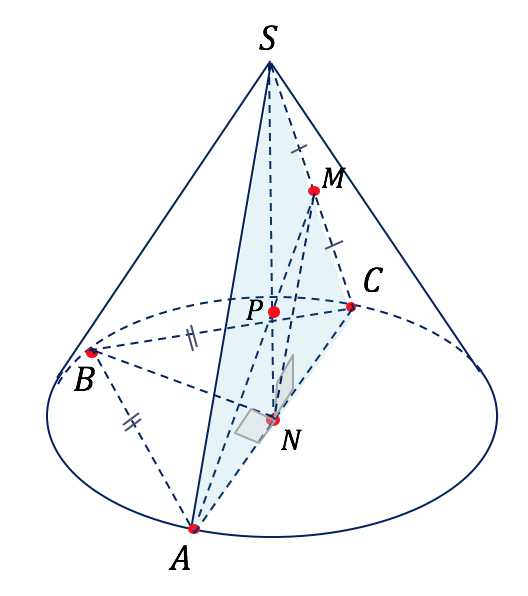
Кроме того, , следовательно, прямая перпендикулярна плоскости и отсюда перпендикулярна любой прямой, лежащей в этой плоскости, и, в частности, прямой . Следовательно, угол — прямой.
б) Найдем угол между прямыми и , при условии, что .
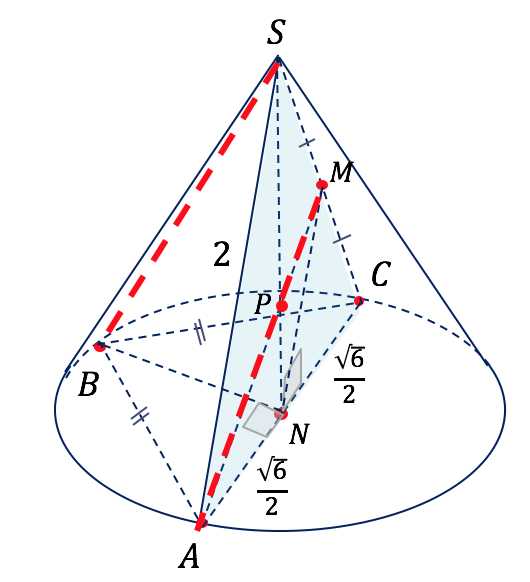
Чтобы найти угол между прямыми, нужно через точку, лежащую на одной из прямых, провести прямую, параллельную второй прямой.
Проведем через точку прямую :
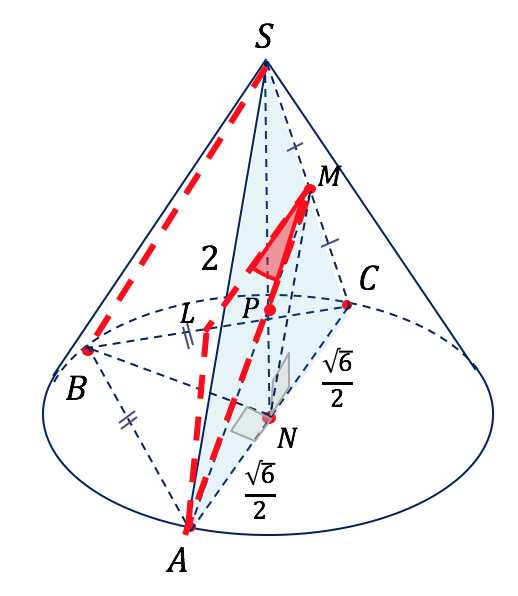
Угол равен углу между прямыми и . Рассмотрим треугольник .
— средняя линия треугольника ; .
— медиана равнобедренного прямоугольного треугольника (угол опирается на диаметр, поэтому он равен ).
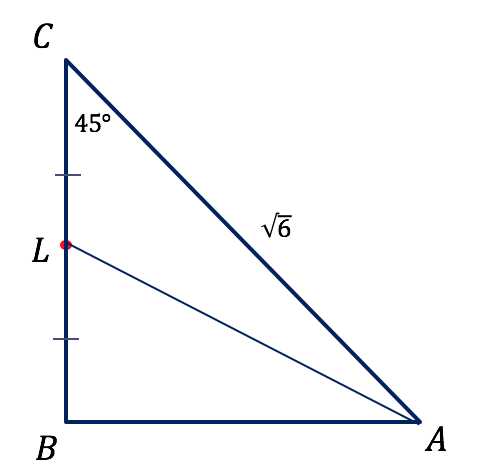
— медиана равнобедренного треугольника .
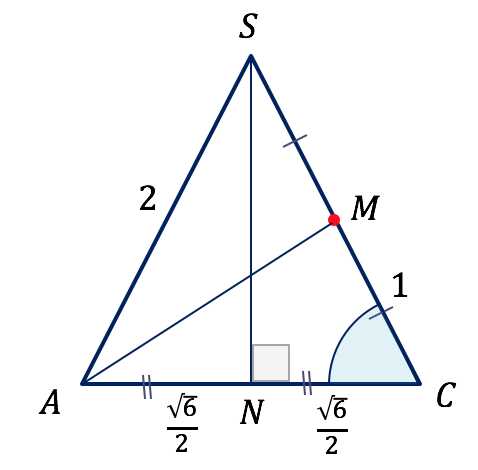
(из прямоугольного треугольника )
найдем по теореме косинусов из треугольника :
;
найдем по теореме косинусов из треугольника .
Следовательно,
Ответ:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
ВИДЕОТЕКА – Репетитор по математике
30. Линейные диофантовы уравнения.
1. Решите уравнение в целых числах.
2. Найдите все целые решения уравнения , удовлетворяющие неравенствам ,
3. В аквариуме у Никиты помимо рыб и улиток живут осьминоги и морские звезды. У осьминога восемь ног, а у морской звезды пять. Никита заметил, что количество морских звезд и осьминогов, взятых вместе, а также количество одних только морских звезд, выражаются двузначными простыми числами. Сколько в аквариуме тех и других, если всего у них 239 ног?
4. Имеются контейнеры двух видов: по 130 кг и по 160 кг. Сколько было контейнеров первого и второго вида, если вместе они весят 3 тонны?
31. 1. Найдите двузначное число, которое на 19 больше суммы квадратов его цифр и на 44 больше удвоенного произведения его цифр.
2. Найдите двузначное число, которое на 44 больше удвоенного произведения его цифр.
3. Найдите все двузначные числа, которые на 9 больше суммы квадратов своих цифр.
4. Найдите все пары двузначных натуральных чисел, одно из которые в два раза меньше другого, такие, что цифры меньшего из них равны сумме и разности.
ege-ok.ru
ОГЭ (ГИА) Задание 26 – Репетитор по математике
№ 324619
В трапеции основания и равны соответственно 36 и 12, а сумма углов при основании равна . Найдите радиус окружности, проходящей через точки и и касающейся прямой , если .
Решение.
показать
№ 324620
Две касающиеся внешним образом в точке окружности, радиусы которых равны 5 и 15, вписаны в угол с вершиной . Общая касательная к этим окружностям, проходящая через точку , пересекает стороны угла в точках и . Найдите радиус окружности, описанной около треугольника .
Решение.
показать
№ 324621
Биссектрисы углов и параллелограмма пересекаются в точке . Найдите площадь параллелограмма, если , а расстояние от точки до стороны равно 4.
Решение.
показать
И. В. Фельдман, репетитор по математике.
ege-ok.ru
ТРИГОНОМЕТРИЯ – Репетитор по математике
В этой статье мы рассмотрим решение тригонометрического уравнения с помощью разложения на множители.
Решить уравнение:
(МГУ, ВМиК, Олимпиада «Абитуриент-2005», 6(6))
Решение. показать
Преобразуем по формуле :
Так как , перепишем уравнение в виде:
Введем замену:
Получим уравнение относительно :
Перейдем к равносильной системе:
Решим первое уравнение системы:
Мы получили уравнение четвертой степени. Чтобы уменьшить коэффициенты, введем еще одну замену: .
Получим уравнение относительно :
Чтобы решить это уравнение, представим левую часть в виде произведение двух квадратных трехчленов с помощью метода неопределенных коэффициентов. (Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.)
Пусть выполняется равенство:
Здесь -целые числа.
Перемножим две скобки справа и приведем подобные члены. Получим:
Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
Приравняем коэффициенты при одинаковых степенях и получим систему уравнений:
, отсюда или
Отсюда
Рассмотрим два случая:
Тогда система примет вид:
Разложим число 12 на множители всеми возможными способами.
Без ограничения общности можем считать, что .
Пусть — подставим в систему, и убедимся, что она не имеет решений.
Аналогично система не имеет решений, если , .
2.
Тогда система примет вид:
Пусть — подставим в систему, и убедимся, что она не имеет решений.
Пусть .
Тогда и наше разложение имеет вид:
Приравняем каждый множитель к нулю, получим корни уравнения :
ege-ok.ru
