Формулы к ЕГЭ по математике
Полный сборник красиво оформленных школьных формул по алгебре и геометрии.
В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.
Смотреть в PDF: Скачайте pdf файл.
Можете записаться на занятия к репетитору математики, если что-то не понятно.
По разделам:
Степени и корни:
Сокращенное умножение:
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители:
Логарифмы:
Формулы тригонометрии, тождества:
Значения тригонометрических функций:
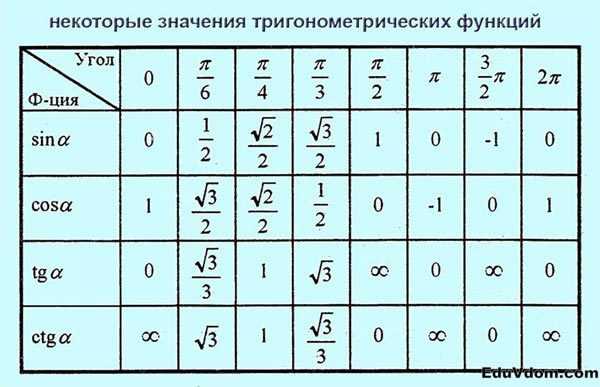
Формулы приведения:
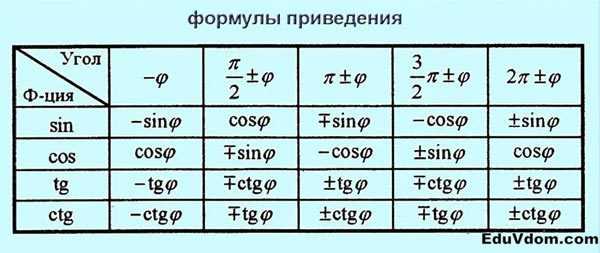
Сумма и разность углов:
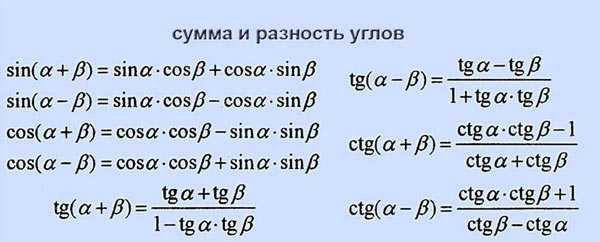
Формулы двойного и тройного аргумента:
Формулы половинного аргумента:
Сумма и разность тригонометрических функций:
Произведение тригонометрических функций:
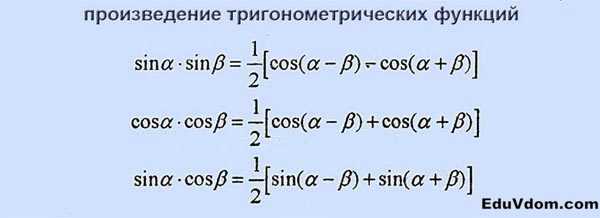
Производная: признаки возрастания, убывания, минимума функции:
Дифференциальное исчисление:
Геометрия: формулы площадей. Прямоугольники, окружности, трапеции:
Стереометрия: объёмы, площади поверхностей:
Обратиться к репетитору по математике.
eduvdom.com
Теория, пособие для подготовки к ЕГЭ по математике
Факт 1.
\(\bullet\) Множество натуральных чисел \(\mathbb{N}\) – это числа \(1,
\ 2, \ 3, \ 4 \ \) и т.д.
\(\bullet\) Рациональные числа \(\mathbb{Q}\) – числа вида \(\dfrac ab\), где \(a\in \mathbb{Z}\), \(b\in \mathbb{N}\). Таким образом, существует включение: \(\mathbb{N}\) содержится в \(\mathbb{Z}\), а \(\mathbb{Z}\) содержится в \(\mathbb{Q}\).
Факт 2.
\(\bullet\) Правила сложения дробей: \[\begin{aligned} &\dfrac ab+\dfrac cb=\dfrac{a+c}b\\[2ex]
&\dfrac ab+\dfrac cd=\dfrac{ad+bc}{bd}\end{aligned}\] Пример: \(\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6\)
\(\bullet\) Правила умножения дробей: \[\dfrac ab\cdot \dfrac cd=\dfrac{ac}{bd}\] Пример: \(\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}\)
\(\bullet\) Правила деления дробей: \[\dfrac ab: \dfrac cd=\dfrac ab\cdot \dfrac dc\] Пример: \(\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76\)
Факт 2.
\(\bullet\) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:
\(\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot
2\llap{/}}{3\cdot
2\llap{/}}=\dfrac{49}3\\[2ex]
&\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot
7\llap{/}}{7\llap{/}\cdot
5}=\dfrac 85\\[2ex]
&\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot
3\cdot
2\llap{/}}=\dfrac{14}{15}\end{aligned}\)
\(\bullet\) Если \(\dfrac ab\) – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель \(b\) делится только на числа \(2\) и \(5\).
Пример: дробь \(\dfrac2{65}\) нельзя представить в виде конечной десятичной дроби, так как \(65=5\cdot 13\), то есть \(\dfrac2{65}=0,0307…\)
дробь \(\dfrac3{160}\) можно представить в виде конечной десятичной дроби, так как \(160=2^5\cdot 5\), то есть \(\dfrac3{160}=0,01875\).
Факт 3.
\(\bullet\) Формулы сокращенного умножения:
\(\blacktriangleright\) Квадрат суммы и квадрат разности: \[(a+b)^2=a^2+2ab+b^2\] \[(a-b)^2=a^2-2ab+b^2\]
\(\blacktriangleright\) Куб суммы и куб разности: \[(a+b)^3=a^3+3a^2b+3ab^2+b^3\quad {\small{\text{или}}}\quad (a+b)^3=a^3+b^3+3ab(a+b)\] \[(a-b)^3=a^3-3a^2b+3ab^2-b^3\quad {\small{\text{или}}}\quad (a-b)^3=a^3-b^3-3ab(a-b)\]
Заметим, что применение данных формул справа налево часто помогает упростить вычисления:
\(13^3+3\cdot 13^2\cdot 7+3\cdot 13\cdot 49+7^3=(13+7)^3=20^3=8000\)
\(\blacktriangleright\) Разность квадратов: \[a^2-b^2=(a-b)(a+b)\]
\(\blacktriangleright\) Сумма кубов и разность кубов: \[a^3+b^3=(a+b)(a^2-ab+b^2)\] \[a^3-b^3=(a-b)(a^2+ab+b^2)\]
Заметим, что не существует формулы суммы квадратов \(a^2+b^2\).
Заметим, что применение данных формул слева направо часто помогает упростить вычисления:
\(\dfrac{7^6-2^6}{7^4+14^2+16}= \dfrac{(7^2-2^2)(7^4+7^2\cdot2^2+2^4)} {7^4+(7\cdot2)^2+2^4}=7^2-2^2=45\)
Факт 4.
\(\bullet\) Квадрат суммы нескольких слагаемых равен сумме квадратов этих слагаемых и удвоенных попарных произведений: \[\begin{aligned}
&(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc\\[2ex]
&(a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd\\[2ex]
&{\small{\text{и т.д.}}}\end{aligned}\]
shkolkovo.net
Какие математические формулы запоминать не стоит
Вы считаете, что чем больше формул знаете, тем спокойнее на экзамене? Так-то оно так, но в случае, если вы дейтвительно понимаете суть формул.
Но если вы коллекционируете формулы, не особо разбираясь в них, не видя связей, следствий, то вряд ли это вас спасет…
Давайте вот прямо сейчас выкинем ряд «лишних» формул из ваших шпаргалок!
Выкидываем из шпаргалки формулу площади правильного треугольника
Наверняка в вашей коллекции есть формула площади правильного треугольника Если вы ее знаете, – рада за вас, если нет, – давайте поймем как ее в два счета вывести.
Вы обязаны знать формулу площади для треугольника со сторонами и углом между ними
А в правильном треугольнике и Вот и получаем требуемую формулу:
Много времени занял вывод формулы?
Выкидываем из шпаргалки формулу площади сектора
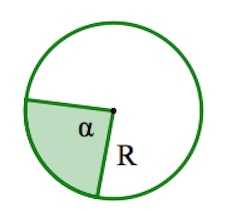
Составим пропорцию
Площадь сектора в (круга) – , какая площадь будет у сектора в градусов находим через пропорцию. Отсюда сразу и получаем формулу.
А в принципе, она и не нужна вовсе… Просто в каждой конкретной задаче вы составляете свою пропорцию.
Например, нужно решить следующую задачу: –> + показать
Найдите центральный угол сектора круга радиуса , площадь которого равна 96. Ответ дайте в градусах.
Решение:
Составляем пропорцию:
Откуда градусная мера центрального угла сектора –
Ответ: 60.
Больше задач – смотрите здесь.
Выкидываем пару формул из таблицы производных
Наверняка, в таблице производных у вас есть такие две строки:
Вы знаете формулу , где – действительное число.
Так разве – это не ?
Аналогично
Кстати, + показать
некоторые абитуриенты, встречая задание, например, , говорят: “не, нас производную от корней не учили брать…”Но мы же должны понимать, что
Выкидываем из шпаргалки формулу боковой поверхности цилиндра
Формула боковой поверхности цилиндра
(где – радиус и высота цилиндра соответственно)
вполне может встретиться в задачах ЕГЭ по математике.
Но ведь что есть боковая поверхность цилиндра в развертке?
Это прямоугольник с одной стороной – , второй стороной, равной длине окружности основания, то есть
Потому и получаем
Выкидываем теорему Пифагора
Шучу, конечно, – кто не знает теорему Пифагора? Но может быть, вам сложно выучить теорему косинусов? Вы подозревали раньше, что теорема Пифагора – частный случай теоремы косинусов?
А ведь в случае прямого угла косинус его будет равен 0, а следовательно, мы и получим теорему Пифагора:
Выкидываем из шпаргалок несколько тригонометрических формул
Не обойтись на ЕГЭ по математике без формул двойного угла для косинуса:
Так вот две последние формулы запоминать нет никакой необходимости. Посмотрите, как быстро выводится, например, средняя формула:
С третьей формулой – аналогично.
Анализируем формулу площади четырехугольника через диагонали
Хорошо бы знать формулу площади четырехугольника с диагоналями и углом между ними …
Тогда набор формул
для квадрата с диагональю ,
для прямоугольника с диагоналями и углом между ними,
для ромба с диагоналями
не придется запоминать!
Становится ясно, что это всего лишь частные случаи формулы (например, в квадрате и , так как ).
Рада, если описанные случаи для вас очевидны –> 😉 + показать
Можно продолжать и далее…
Но пока все! Вам есть что сказать/спросить? Пишите в комментариях.
egemaximum.ru
Все формулы по математике | oge-ege.info
Дорогой друг, примите мои рекомендации по распечатке формул. Итак, вы скачали архив. Он малюсенький, поэтому, просто кликнув 2 раза на папку с материалами, вы сразу получаете pdf файл (или открываете папку с сохраненным pdf файлом). Нажимаем Файл→Печать. Должна быть видна (галочка стоит) готовность вашего принтера к работе. Нажимаем Настройка→Функции. Указываете параметры цвета по своему усмотрению (не принципиально), Страниц на листе — выбираете 2 стр на листе.
Здесь же Ярлыки печати. Выбираем: По умолчанию.
Здесь же Дополнительно. Если имеется хоть одна галочка в любой из 2-х клеток — убираем. ОК. Оказываемся опять в меню Печать. Выбираем: Страницы и через запятую (без пробела) указываем 16,1. Нажимаем кнопку печать. Распечаталось, не трогаем лист, только поправляем его слегка, для следующей печати. Нажимаем: Файл-Печать-Страницы-2,15-Печать. Вот один лист А4 готов. Вставляем в принтер новый лист и печатаем страницы 14,3. Слегка поправив, на этом же листе (нажимаем: Файл-Печать-Страницы-4,13-Печать).Готово. Далее на третьем листе А4 напечатаем 12,5 и 6,11. И, наконец, на последнем листе распечатаем страницы 10,7 и 8,9. Надеюсь, все получилось!
И вот еще что!
Если вы — любитель маленьких справочников, то получите инструкцию по распечатке моего сборника формул в уменьшенном формате: по 4 страницы на листе А4.
Итак, вы открыли файл .pdf с «Основными формулами математики 7-11″. Нажимаете Файл→Печать. Нажимаем Настройка→Функции. Указываете параметры цвета по своему усмотрению (не принципиально), Страниц на листе — выбираете 4 стр на листе.
Здесь же Ярлыки печати. Выбираем: По умолчанию.
Здесь же Дополнительно. Если имеется хоть одна галочка в любой из 2-х клеток — убираем. Нажимаем ОК. Оказываемся опять в меню Печать. Выбираем: Страницы и через запятую (без пробелов!) указываем 16,1,14,3. Нажимаем кнопку Печать. Распечаталось, поворачиваем лист на 180º (текст вверху, т. е. нам виден). Опять Файл→Печать→Страницы и вводим через запятую без пробелов 2,15,4,13. Нажимаем кнопку Печать. Вот первый лист А4 готов. Вставляем в принтер новый лист. Файл→Печать→Страницы и вводим: 10,7,12,5. Нажимаем кнопку Печать. Распечатанный лист поворачиваем на 180º (напечатанное вверху) и Файл→Печать→Страницы, вводим без пробелов через запятую: 8,9,6,11. Печать. Получили второй лист А4. Теперь аккуратно разрежьте каждый из двух листов А4 поперек, подровняйте и сверните в книжечку!
Еще раз ссылка на скачивание формул. Уверена, что у вас все получится! Учите формулы поэтапно: скажем, сегодня с 1-ой по 23-ю и т.д. Помните: ЗНАНИЕ — СИЛА! Дорогу осилит идущий!
