246 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Найдите все значения параметра , при которых система $$\left\{\begin{matrix}\log_{2} (3-x+y)=\log_{2} (25-6x+7y)\\ y+2=(x-2a)^{2}+a+2x\end{matrix}\right.$$ имеет ровно два решения
Рассмотрим область определения данной системы. Так как даны логарифмы, то: $$\left\{\begin{matrix}3-x+y>0\\25-6x+7y>0\end{matrix}\right.\Rightarrow$$ $$\left\{\begin{matrix}y>x-3\\y>\frac{6x-25}{7}\end{matrix}\right.$$ (желтым выделено решение для первого неравенства, синим — для второго, серым — их пересечение)
Рассмотрим первое уравнение системы:
$$\log_{2}(8(3-x+y))=\log_{2}(25-6x+7y)\Leftrightarrow$$$$24-8x+8y=25-6x+7y\Leftrightarrow$$$$y=2x+1 (1)$$
Построим график данной функции с учетом области определения:
Как видим, чтобы было два пересчения, x должен быть больше 4 (иначе часть прямой лежит вне области определения)
Подставим (1) во второе:$$2+2x+1=(x-2a)^{2}+a+2x\Leftrightarrow$$$$(x-2a)^{2}=3-a$$
Так как число в квадрате, то правая часть уравнения должна быть больше нуля (если равна нулю, то корень всего один): $$3-a>0\Rightarrow a<3$$
Рассмотрим график второгой функции:
$$y+2=x^{2}-4ax+2a^{2}+a+2x\Leftrightarrow$$$$y=x^{2}+x(2-4a)+4a^{2}+a-2$$
Найдем вершину параболы:
$$x_{0}=-\frac{2(1-2a)}{2}=2a-1$$
$$y_{0}=4a^{2}-4a+1-2(2a-1)^{2}+4a^{2}+a-2=8a^{2}-3a-1-8a^{2}+8a-2=5a-3$$
Рассмотрим возможное расположение графика с учетом области определения:
Как видим, координата y вершины параболы должна быть больше -8, а х больше -3 (если будет левее, то отно пересечение точно не попадет в область определения) :
$$\left\{\begin{matrix}2a-1>-3\\5a-3>-8\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a>-1\\a>-1\end{matrix}\right.$$
С учетом того, что $$a<3$$, получаем: $$a \in (-1;3)$$
mathlesson.ru
248 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
При изучении темы «Среднее арифметическое» в классе из 34 учащихся раздали синие и красные карточки, при этом каждый из учеников получил хотя бы одну карточку, но не более одной каждого цвета. На каждой карточке написано одно целое число от 0 до 20 (на различных карточках могут быть записаны одинаковые числа). Среднее арифметическое по всем розданным карточкам оказалось равным 15 по каждому цвету в отдельности. Затем каждый ученик назвал наибольшее из чисел на своих карточках (если ему досталась одна карточка, то он назвал число, написанное на этой карточке). Среднее арифметическое всех названных чисел оказалось равно S.
а) Приведите пример, когда S<15
б) Могло ли S быть равным 9?
в) Найдите наименьшее значение S , если по две карточки получили 17 учеников.
A) Пусть у 30 человек и синие, и красные , но каждой из которых по 16 , у двух синие с О и у двух красных с О
Синие: $$\frac{30*16+2*0}{32}=15$$
Красные :$$\frac{30*16+2*0}{32}=15$$
Условие среднего арифметического выполняются : $$S=\frac{30*16+4*0}{34}<15\Rightarrow$$ да
Б) Пусть:
k людей , у которых и синие и красные
a-сумма всех чисел у людей только с одной карточкой
b-сумма максимальных чисел у людей с двумя карточками
c-минимальных
Так как средняя для синих и красных отдельно составляет 15, то и среднее для всех вообще чисел равно 15.
При этом всего было выдано $$34+k$$ карточек. Значит общая сумма $$15(34+k)=510+15k$$ . С другой стороны эту же сумму можно представить как $$a+b+c$$: $$a+b+c=510+15k(1)$$. При этом $$a+b=9*34=306$$ . Подставим в (1): $$306+c=510+15k\Leftrightarrow$$ $$c=204+15k$$
С другой стороны $$c\leq 20k$$ ( сумма наименьших будет максимальна если на всех карточках число 20)
Получаем: $$204+15k\leq 20k\Leftrightarrow$$ $$5k\geq 204\Leftrightarrow$$ $$k\geq 40,8$$ но $$k\leq 34$$, следовательно , нет.
B) Аналогично, $$a+b =34S, a+b+c=15(34+17)$$.Тогда $$34S+c=765\Rightarrow$$ $$S=\frac{765-c}{34}$$. Очевидно , что $$S\Rightarrow min$$, при $$c\Rightarrow max$$, т.е. $$S\geq \frac{765-17*20}{34}=12,5$$
Найдем такой пример :
У нас 17 человек с карточками красными и синими на каждой из которых по 20, тогда сумма на все оставшиеся карточки (по одной) составит :
$$765-2*340=85$$. При этом она приходится на 17 человек с одной карточкой . Пусть y-сумма на синих, тогда 85-y-на красных. Учитывая среднее 15 для синих и красных :
$$\left\{\begin{matrix}340+y=15(17+N)\\340+85-y=15(17+17-N)\end{matrix}\right.$$, Где N-число синих , тогда красных 17-N (речь идет об одиночных карточках)
$$\left\{\begin{matrix}\frac{340+y}{15}=17+N\\\frac{425-y}{15}=34-N\end{matrix}\right.$$
Слева должны быть натуральные числа, т.е. 340+y и 435-y делятся нацело на 15 . При y=20 получим :
$$\frac{340+20}{15}=\frac{360}{15}=24=17+N\Rightarrow N=7$$
$$\frac{425-20}{15}=27$$
Условия выполнились, следовательно , если у 17 человек синие и красные с числами 20, у 17 человек только синие с общей суммой 20( например 1+2+3+4+5+2+3) и у 10 только красных с суммой 65 (7+7+7+7+7+7+7+7+7+2), то S=12,5
mathlesson.ru
243 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
А) Существует ли натуральное число n, делящееся нацело на 12 и при этом имеющее ровно 12 различных делителей (включая единицу и само число n)?
Б) Найдите все натуральные числа, делящиеся нацело на 14 и имеющие ровно 14 различных натуральных делителей.
В) Существует ли натуральное число, делящееся нацело на 2014 и имеющее ровно 2014 различных натуральных делителей?
a) Пусть число $$N=a_{1}^{\alpha _{1}}*a_{2}^{\alpha _{2}}…a_{n}^{\alpha _{n}}$$
Тогда количество делителей данного числа составит: $$M=(\alpha _{1}+1)(\alpha _{2}+1)…(\alpha _{n}+1)$$
Разложим число 12 на множители:$$12=2*2*3=2^{2}*3^{1}(1)$$. То есть, чтобы число N делилось нацело на 12, среди множителей $$a_{1}..a_{n}$$ данного числа должны встретиться 2 со степенью, кратной 2 и 3 с любой степенью. С другой стороны, необходимо 12 множителей, то есть $$(\alpha _{1}+1)(\alpha _{2}+1)…(\alpha _{n}+1)=12$$ или $$12=2*2*3=(\alpha _{1}+1)(\alpha _{2}+1)…(\alpha _{n}+1)(2)$$. То есть мы имеем произведение трех чисел, следовательно, количество множителей будет не более 3.
Рассмотрим вариант с тремя множителями, то есть $$N=2^{2\alpha _{1}}*3^{\alpha _{2}}*a_{3}^{\alpha _{3}}$$
Раз три множителя, то с учетом разбиения (1) получим, что множители будут 2,3 и еще любой другой (не кратный 2 и 3), пусть будет 5, при этом с учетом равенства (2) получим степени 2,1 и 1, то есть : $$N =2^{2}*3^{1}*5^{1}=60$$
б) Аналогично рассуждаем: $$N=a_{1}^{\alpha _{1}},a_{2}^{\alpha _{2}}…a_{n}^{\alpha _{n}}$$. $$14=2*7\Rightarrow$$ есть делитель 2 и 7 , следовательно $$N=2^{\alpha _{1}}*7^{\alpha _{2}}*a_{n}^{\alpha _{n}}$$. Пусть $$(\alpha _{1}+1)=2$$ и $$(\alpha _{2}+1)=7$$, тогда $$\alpha _{1}=1 ; \alpha _{2}=6$$. То есть числа : $$N=2*7^{6}$$ или $$7*2^{6}$$
в) Аналогично 2014=2*19*53. То есть среди множителей есть 2,19 и 53. Пусть $$2014=2^{m}*19^{n}*53^{l}$$, тогда $$(m+1)(n+1)(l+1)=2014=2*19*53\Rightarrow m=1, n=18, l=52$$
mathlesson.ru
224 вариант Алекса Ларина. Разбор ЕГЭ математика 2018.
Радиус вписанной в треугольник АВС окружности равен $$\frac{\sqrt{15}}{3}$$. Окружность радиуса $$\frac{5\sqrt{5}}{3\sqrt{3}}$$ касается вписанной в треугольник АВС окружности в точке Т, а также касается лучей, образующих угол АСВ. Окружности касаются прямой АС в точках К и М.
А) Докажите, что треугольник КТМ прямоугольный
Б) Найдите тангенс угла АВС, если площадь треугольника АВС равна $$3\sqrt{15}$$, а наибольшей из его сторон является сторона АС.
а) Через Т строим общую касательную $$TL\cap MK=L$$; $$ML=LT$$; $$TL=LK$$ (по свойству касательных) $$\Rightarrow$$ $$ML=TL=LK$$ $$\Rightarrow$$ т.к. TL — медиана, то $$\bigtriangleup MTK$$ — прямоугольный
б) 1) Пусть $$O_{2}H\perp O_{1}M$$ $$\Rightarrow$$ $$HO_{2}=MK$$; $$O_{1}H=O_{1}M-O_{2}K=\frac{5\sqrt{5}}{3\sqrt{3}}-\frac{\sqrt{5}}{\sqrt{3}}=\frac{2\sqrt{5}}{3\sqrt{3}}$$
2) $$O_{1}O_{2}=O_{1}T+TO_{2}=\frac{8\sqrt{5}}{3\sqrt{3}}$$
3) из $$\bigtriangleup O_{1}O_{2}H$$: $$O_{2}H=\sqrt{O_{1}O_{2}^{2}-O_{1}H^{2}}=\frac{10}{3}$$
4) Пусть $$KC=a$$; $$\bigtriangleup O_{1}CM\sim\bigtriangleup O_{2}CK$$: $$\frac{O_{1}M}{O_{2}K}=\frac{MC}{KC}$$ $$\Leftrightarrow$$ $$\frac{5\sqrt{5}}{3\sqrt{3}}\div\frac{\sqrt{5}}{\sqrt{3}}=\frac{\frac{10}{3}+x}{x}$$; $$5x=10+3x$$ $$\Leftrightarrow$$ $$x=5$$
5) $$\tan\angle O_{1}CM=\frac{O_{2}K}{KC}=\frac{\sqrt{5}}{\sqrt{3}\cdot5}=\frac{1}{\sqrt{15}}$$ $$\Rightarrow$$ т.к. $$CO_{2}$$ — биссектриса, то $$\angle ACB=\frac{2\cdot\frac{1}{\sqrt{15}}}{1-(\frac{1}{\sqrt{15}})^{2}}=\frac{\sqrt{15}}{7}$$ $$\Rightarrow$$ т.к. $$1+\tan^{2}\alpha=\frac{1}{\cos^{2}\alpha}$$, то $$\cos\angle ACB=\sqrt{\frac{1}{1+\frac{\sqrt{15}}{7}}}=\frac{7}{8}$$
6) Пусть $$AT=AK=x$$; $$TB=BR=y$$, тогда: $$S_{ABC}=\sqrt{p\cdot(p-a)(p-b)(p-c)}=3\sqrt{15}$$; $$p=\frac{2x+2y+10}{2}=(x+y+5)$$; $$a=x+5$$; $$b=y+5$$; $$c=x+y$$; $$\sqrt{(x+y+5)5xy}=3\sqrt{15}$$; $$(x+y+5)xy=27(1)$$
7) По т. косинусов: $$AB^{2}=AC^{2}+BC^{2}-2AC\cdot BC\cos ACB$$; $$(x+y)^{2}=(5+x)^{2}+(5+y)^{2}-2(5+x)(5+y)\cdot\frac{7}{8}$$; $$x^{2}+2xy+y^{2}=25+10x+x^{2}+25+10y+y^{2}-\frac{7}{4}(25+5x+5y+xy)$$; $$50+10(x+y)-\frac{7}{4}(25+5(x+y)+xy)-2xy=0(2)$$
Решим систему уравнений 1 и 2: замена $$x+y=a$$; $$xy=b$$:
$$\left\{\begin{matrix}b(a+5)=27\\50+10a-\frac{7}{4}(25+5a+b)-2b=0\end{matrix}\right.$$.
Рассмотрим 2ое: умножим на 4: $$200+40a-175-35a-7b-8b=0$$; $$5a+25=15b$$; $$a+5=3b$$
Подставим в 1ое, умноженное на 3: $$3b(a+5)=81$$; $$(a+5)(a+5)=81$$ $$\Leftrightarrow$$ $$a+5=9$$ $$\Leftrightarrow$$ $$a=4$$; $$b=\frac{4+5}{3}=3$$. Получаем: $$\left\{\begin{matrix}x+y=4\\xy=3\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=1\\y=3\end{matrix}\right.$$ или $$\left\{\begin{matrix}x=3\\y=1\end{matrix}\right.$$
Т.к. по условию АС самая большая, то $$x=1$$; $$y=3$$ не подходит; $$\Rightarrow$$ $$x=3$$; $$y=1$$
8) из $$\bigtriangleup BRO_{2}$$: $$\tan O_{2}BR=\frac{O_{2}R}{BR}=\frac{\frac{\sqrt{5}}{\sqrt{3}}}{1}=\frac{\sqrt{5}}{\sqrt{3}}$$; $$\tan ABC=\frac{\frac{2\sqrt{5}}{\sqrt{3}}}{1-(\frac{\sqrt{5}}{\sqrt{3}})^{2}}=\frac{2\sqrt{5}}{\sqrt{3}}\cdot\frac{-3}{2}=-\sqrt{15}$$
mathlesson.ru
ОГЭ математика 2019. Разбор варианта Алекса Ларина № 197.
В треугольнике КЕМ длина стороны КЕ равна 27, длина биссектрисы КВ равна 24, а длина отрезка МВ равна 8. Найдите периметр треугольника КМВ.
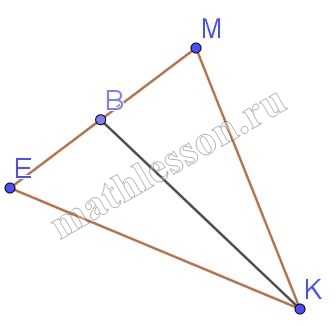
1) Пусть KE=a=27; KM=b; EB=x; BM=y=8; KB=m=24; $$\angle EKB=\angle BKM=\alpha$$
2) По свойству биссектрисы: $$\frac{x}{y}=\frac{a}{b}(1)$$
3) Рассмотрим теорему косинусов для $$\Delta EBK$$ и $$\Delta BMK$$:
$$\left\{\begin{matrix}y^{2}=m^{2}+b^{2}-2mb \cos \alpha\\x^{2}=m^{2}+a^{2}-2ma \cos \alpha\end{matrix}\right.$$
Умножим первое и второе уравнения на a и b соответственно и вычтем из первого второе :
$$\left\{\begin{matrix}y^{2}a =m^{2}a+b^{2}a-2mab \cos \alpha\\x^{2}b=m^{2}b+a^{2}b-2mab \cos \alpha\end{matrix}\right.$$
Получим: $$y^{2}a-x^{2}b=m^{2}a+b^{2}a-m^{2}b-a^{2}b$$
Рассмотрим левую часть равенства: $$y^{2}a-x^{2}b=xy(\frac{ya}{x}-\frac{xb}{y})$$ .С учетом , что $$\frac{x}{y}=\frac{a}{b}$$, получим : $$xy(\frac{b}{a}*a-\frac{a}{b}*b)=xy(b-a).$$
Рассмотрим правую часть равенства: $$m^{2}a+b^{2}a-m^{2}b-a^{2}b=m^{2}(a-b)-ba(a-b)$$. Получим : $$xy(b-a)=m^{2}(a-b)-ba(a-b)$$.
Т.к. $$a\neq b$$ (иначе получим равнобедренный), то поделим $$a-b$$: $$-xy=m^{2}-ba\Rightarrow m^{2}=ab-xy(2)$$ — вообще, это формула длины биссектриссы через две стороны и отрезки третьей, но в учебниках за 7-9 класс ее не встречал, потому необходимо ее выводить.
4) Итого имеем систему: $$\left\{\begin{matrix}\frac{x}{y}=\frac{a}{b}\\m^{2}=ab-xy\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{x}{8}=\frac{27}{b}\\24^{2}=27b-8x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{216}{b}\\576=27b-\frac{8*216}{b}\end{matrix}\right.$$
$$576b=27b^{2}-1728\Leftrightarrow$$ $$27b^{2}-576b-1728=0|:9\Leftrightarrow$$ $$3b^{2}-64b-192=0$$
$$D=4096+2304=6400$$
$$b_{1}=\frac{64+80}{6}=\frac{144}{6}=24$$
$$b_{2}=\frac{64-80}{6}<0$$
5) $$P_{BMK}=m+y+b=24+8+24=56$$
mathlesson.ru
238 вариант Алекса Ларина. Разбор ЕГЭ математика 2018.
Найдите все значения параметра $$3a(a-7)-8(a-7)(2^{x}+1)\leq (8x^{2}-16x)(2^{x}+1)-3ax^{2}+6ax$$ , при каждом из которых неравенство имеет решения на промежутке $$[-1;0)$$
Преобразуем данное неравенство: $$(a-7)(3a-8(2^{x}+1))\leq 8x(x-2)(2^{x}+1)-3ax(x-2) \Leftrightarrow$$$$(a-7)(3a-8(2^{x}+1))\leq x(x-2)(8(2^{x}+1)-3a) \Leftrightarrow$$$$(a-7)(3a-8(2^{x}+1)) + x(x-2)(3a-(2^{x}+1))\leq 0 \Leftrightarrow$$$$(8(2^{x}+1)-3a)(x^{2}-2x+a-7) \geq 0 (1)$$
Рассмотрим по отдельности обе скобки и представим их как функции $$a(x)$$:
$$8(2^{x}+1)-3a = 0\Leftrightarrow$$$$a=\frac{2^{x+3}}{3}+\frac{8}{3}$$ — график степенной функции
$$x^{2}-2x+a-7=0 \Leftrightarrow$$$$a=-x^{2}+2x+7\Leftrightarrow$$$$a=-(x^{2}-2x-7)\Leftrightarrow$$$$a=-(x^{2}-2x+1-1-7)\Leftrightarrow$$$$a=-(x-1)^{2}+8$$ — график квадратичной функции.
По условии задачи необходимо, чтобы решения были на промежутке $$[-1;0)$$, тогда так же построим графики $$x=-1 ; x=0$$ и графики полученных функции в системе координат AoX.
Найдем пересечение степенной функции с прямыми $$x=-1 ; x=0$$:
$$x=-1 ; a(-1)=\frac{2^{-1+3}}{3}+\frac{8}{3}=4$$
$$x=0 ; a(0)=\frac{2^{0+3}}{3}+\frac{8}{3}=\frac{16}{3}$$
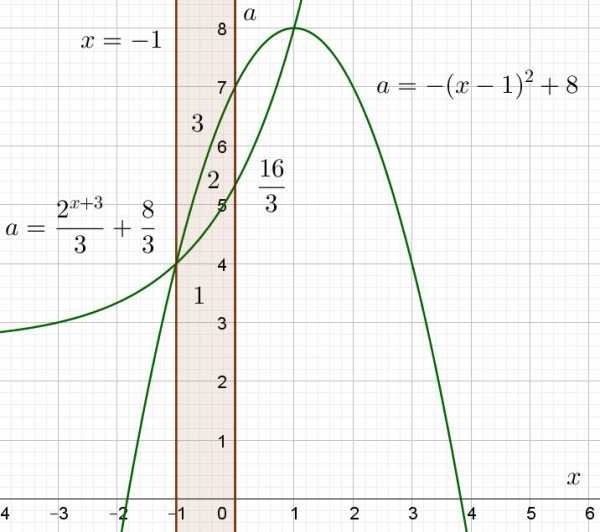
Как видим по графикам мы получили три области, необходимо проверить, точки каких областей удовлетворяют неравенству (1). Для этого будем брать из каждой области точку, и подставлять координаты в наше неравенство:
1) Возьмем точку (0;0) : $$(8(2^{0}+1)-3*0)(0^{2}-2*0+0-7) \geq 0 \Leftrightarrow$$$$16*(-7)\geq 0$$ — неравенство неверно, следовательно, первая область не подходит
2) Возьмем точку (0;6): $$(8(2^{0}+1)-3*6)(0^{2}-2*0+6-7) \geq 0 \Leftrightarrow$$$$-2*(-1)\geq 0$$ — неравенство верно, следовательно, вторая область подходит и по а она находится в промежутке [4;7) (7 не входит, так как по условию $$x \neq 0$$)
3) Возьмем точку (0;8) : $$(8(2^{0}+1)-3*8)(0^{2}-2*0+8-7) \geq 0 \Leftrightarrow$$$$-8*1 \geq 0$$ — неравенство неверно, следовательно, третья область не подходит
Итоговый ответ: $$a \in \left [ 4 ; 7 \right )$$
mathlesson.ru
