ЕГЭ по информатике задание 18.Отрезки — Информатика в школе
ЕГЭ по информатике задание 18.Отрезки
Тема: «Логика и теория множеств»
На числовой прямой даны два отрезка: Р = [37; 60] и Q = [40; 70]. Укажите наименьшую возможную длину такого отрезка А, что формула
\( (x\in P) \to (((x\in Q) \land \neg ( x\in A))\to\neg ( x\in P)) \)
РЕШЕНИЕ
Еще один вид задания ЕГЭ по информатике задание 18
Для наглядности задачи ЕГЭ по информатике построим отрезки:
Введем обозначения:
\[ (x\in A) \equiv A; (x\in P) \equiv P; (x\in Q) \equiv Q \]
Перепишем формулу:
\[ (x\in P) \to (((x\in Q) \land \neg ( x\in A))\to\neg ( x\in P)) = P \to ((Q \land \neg A) \to \neg P) \]
Заменяем логическое следование на логическое умножение по формуле:
\[ A \to B = \neg A \vee B \]
\[ P \to ((Q \land \neg A) \to \neg P) = \neg P \vee ((Q \land \neg A) \to \neg P) = \neg P \vee \neg(Q \land \neg A) \vee \neg P = \]
\[ =\neg P \vee \neg Q \vee A \]
После упрощения формулы построим отрезки, исходя из преобразованной формулы :
Логическое ИЛИ истинно, если истинно хотя бы одно утверждение. Условию ¬P ∨ ¬Q = 1 удовлетворяют лучи (−∞, 40) и (60, ∞). Поскольку выражение ¬P ∨ ¬Q ∨ A должно быть тождественно истинным, выражение A должно быть истинно на отрезке [40, 60].
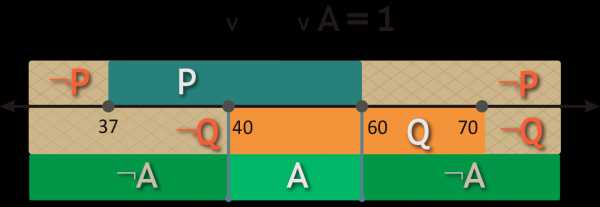
Остается посчитать длину отрезка A: 60 — 40 = 20
Еще один способ решения через таблицы истинности:
| Интервалы | P | Q | ¬P | ¬Q | ¬P ∨ ¬Q | A |
| [ −∞; 37 ] | 0 | 0 | 1 | 0 | 1 | 1 |
| [ 37; 40 ] | 1 | 0 | 0 | 1 | 1 | 1 |
| [ 40; 60 ] | 1 | 1 | 0 | 0 | 0 | 0 |
| [ 60; 70 ] | 0 | 1 | 1 | 0 | 1 | 1 |
| [ 70; ∞ ] | 0 | 0 | 1 | 1 | 1 | 1 |
Как видно выражение ¬P ∨ ¬Q будет истинно в любом случае, кроме интервала [ 40; 60 ]. Истинность этого интервала зависит от отрезка А, т.к. выражение ¬P ˅ ¬Q ложно. Таким образом, область истинности выражения должна перекрывать отрезок [ 40 ; 60 ]. Наименьшая возможная длина отрезка А = 20.
Ответ: 20
P.S.Не забудьте подписаться на новости, чтобы ничего не пропустить:
amlesson.ru
Решение задания 18 егэ по информатике с помощью таблиц истинности
Л. И. Мазничевская
средняя общеобразовательная школа № 763, Москва
Решение задания 18 ЕГЭ ПО ИНФОРМАТИКЕ С ПОМОЩЬЮ ТАБЛИЦ ИСТИННОСТИ
Аннотация
В статье представлены материалы, предназначенные для использования учителями информатики при подготовке учащихся к ЕГЭ по информатике.
К сожалению, правильно решают задание 18 ЕГЭ по информатике малая часть учащихся. Это связано с тем, что предлагаются различные способы решения этого задания, но эти способы применимы только на некотором сегменте заданий.
В представленных вашему вниманию материалах четыре различных типа задач решаются с помощью составления таблиц истинности. Все задачи выбраны из заданий для тренировки с известного сайта К. Ю. Полякова[1].
Ключевые слова: информатика, таблица истинности, алгоритм, законы алгебры логики, импликация.
Контактная информация
Мазничевская Лариса Ивановна, учитель информатики высшей категории, государственное бюджетное общеобразовательное учреждение города Москвы “Школа № 763”, адрес: 129346, г. Москва, ул. Стартовая, д. 27, к. 3; телефон: (495) 474-90-60; e-mail: mli97@inbox.ru
При решении любого задания 18 ЕГЭ по информатике необходимо знать основные понятия и законы математической логики, а также выполнить следующие шаги алгоритма:
определение элементарных высказываний
замена переменных (при необходимости)
раскрытие импликации или эквивалентности
преобразование с использованием законов алгебры логики
построение таблиц истинности
запись ответа.
Задача 1(105 Поляков)
На числовой прямой даны два отрезка: P = [44; 49] и Q = [28; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Решение:
Введем обозначения и упростим выражение:
=P Q
Вся числовая ось распадается на интервалы, построим таблицу истинности для одного из значений заданного интервала для полученной формулы
| Интервал | Значение Х | P | Q | | А | Итог |
| (-;28] | 20 | 0 | 0 | 1 | 0 | 1 |
| [28;44] | 30 | 0 | 1 | любое | любое | 1 |
| [44;49] | 48 | 1 | 1 | любое | любое | 1 |
| [49;53] | 50 | 0 | 1 | любое | любое | 1 |
| [53;+] | 54 | 0 | 0 | 1 | 0 | 1 |
Так как нам нужна наибольшая возможная длина такого отрезка A, чтобы формула
была тождественно истинна, то есть принимала значение 1 при любом значении переменной х, то А принимает значение истинно на [28;53], длина этого отрезка равна 53-28=25
Ответ: 25
Задача 2(135 Поляков)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа
ДЕЛ(x, A) (ДЕЛ(x, 14) ДЕЛ(x, 21))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решение:
Упростим выражение:
ДЕЛ(x, A) (ДЕЛ(x, 14) ДЕЛ(x, 21))= ДЕЛ(x, A) ДЕЛ(x, 14) ДЕЛ(x, 21)
Определим числа, входящие во множество ДЕЛ(x, 14) и ДЕЛ(x, 21): 14, 21, 28, 42, 56,63…
Построим таблицу истинности для формулы ДЕЛ(x, A) ДЕЛ(x, 14) ДЕЛ(x, 21)
| Число Х | ДЕЛ(x, 14) | ДЕЛ(x,21) | ДЕЛ(x, 14) ДЕЛ( x, 21) | Х не кратно А | А | Итог |
| 14 | 1 | 0 | 0 | 1 | 0 | 1 |
| 21 | 0 | 1 | 0 | 1 | 0 | 1 |
| 28 | 1 | 0 | 0 | 1 | 0 | 1 |
| 42 | 1 | 1 | 1 | любое | любое | 1 |
| 56 | 1 | 0 | 0 | 1 | 0 | 1 |
Необходимо выбрать первое значение А, при котором высказывание «Х не кратно А»может принимать любое значение Х=42, оно является наименьшим.
Ответ: 42
Задача 3(150 Поляков)
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение
(X &
56 0) ((X & 48 = 0) (X & A 0))тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Решение:
Для удобства введем обозначения и упростим выражение
56= X & 56 0
48=X & 48 0
A= X & A 0
(X & 56 0) ((X & 48 = 0) (X & A 0))=56 ( 48 A ) = А
Переведем в двоичную систему счисления числа 18, 54
5610=1110002
4810=1100002
Искомое число х – разрядное слагаемое двоичной системы счисления из множества {1, 2, 4,8,16,32}. Построим таблицу истинности
| Число Х, его двоичный код | 1110002 | X & 48 0 1100002 | А X & A 0 | Итог |
| 1, 000001 | 1 | 0 | Любое(0 или1) | 1 |
| 2, 000010 | 1 | 0 | Любое(0 или1) | 1 |
| 4, 000100 | 1 | 0 | Любое(0 или1) | 1 |
| 8, 001000 | 0 | 0 | 1 | 1 |
| 16, 010000 | 0 | 1 | Любое(0 или1) | 1 |
| 32, 100000 | 0 | 1 | Любое(0 или1) | 1 |
Из таблицы х=8, оно является наименьшим
Ответ: 8
Задача 4(88 Поляков)
Элементами множества А являются натуральные числа. Известно, что выражение
(x {2, 4, 6, 8, 10, 12}) → (((x {3, 6, 9, 12, 15}) ¬(x A)) → ¬(x {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Решение:
Для удобства введем обозначения и упростим выражение
В=x {2, 4, 6, 8, 10, 12}
С= x {3, 6, 9, 12, 15}
А= x A
(x {2, 4, 6, 8, 10, 12}) → (((x {3, 6, 9, 12, 15}) ¬(x A)) → ¬(x {2, 4, 6, 8, 10, 12}))=B→((C ¬A) → ¬B) = ¬B((C ¬A) → ¬B)= ¬B¬C ¬A) ¬B= ¬B¬C
Построим таблицу истинности
| Число Х | ¬B | ¬C | A | Итог |
| 2 | 0 | 1 | любое(0 или1) | 1 |
| 3 | 1 | 0 | любое(0 или1) | 1 |
| 4 | 0 | 1 | любое(0 или1) | 1 |
| 6 | 0 | 0 | 1 | 1 |
| 8 | 0 | 1 | любое(0 или1) | 1 |
| 9 | 1 | 0 | любое(0 или1) | 1 |
| 10 | 0 | 1 | любое(0 или1) | 1 |
| 12 | 0 | 0 | 1 | 1 |
| 15 | 1 | 0 | любое(0 или1) | 1 |
6+12=18
Ответ: 8
Литература
http://kpolyakov.spb.ru/school/probook.htm
videouroki.net
КАК НАУЧИТЬ РЕШАТЬ ЗАДАНИЕ 18 ЕГЭ ПО ИНФОРМАТИКЕ
Белова Т.В.как научить решать задание 18 егэ по информатике
муниципальное бюджетное общеобразовательное учреждение «Лицей»,
г. Арзамас, ya.bellova.tatyana@yandex.ru
Перед тем как приступать к решению заданий 18 «Проверка истинности логического выражения» экзаменационной работы по информатике, нужно объяснить (или вспомнить) учащимся, что такое понятие «объединение» и «пересечение» нескольких множеств. И так как задание 18 связано с определением отрезков, то и лучше всего эти понятия объяснять на отрезках. Но связать необходимо эти понятия с понятиями алгебры логики – «конъюнкция» и «дизъюнкция», ну и, конечно же, «инверсия». Приведу это все на примере. Для начала рассмотрим инверсию отрезка, или, проще говоря, отрицание отрезка.
Дан отрезок P=[6,15]. Найти отрезки, которые будут инверсией отрезка P=[6,15]. Рассмотрим координатную прямую (рис. 1):
ᄃ
рис. 1
На прямой отмечаем отрезок P (синяя область), тогда понятно, что промежутки не P будут промежутки и (зеленая область) – рис. 1. Обращая внимание, что точки 6 и 15 в инверсию отрезка входить не будут.
Рассмотрим еще пример: даны два отрезка P=[6,15] и Q=[8,25]{приведены те же обозначения, что и в задании ЕГЭ, чтобы учащиеся сразу привыкали к обозначениям}. Найти отрезок, который будет обозначать конъюнкцию (объединение) и дизъюнкцию (пересечение) этих отрезков
Рисуем отрезки на координатной прямой (рис. 2):
15
8
25
рис. 2
Сначала отмечаем области на координатной прямой, которые обозначают отрезки P (синий цвет) и Q (желтый цвет). Затем определяем, какая часть координатной прямой будет служить конъюнкцией этих двух отрезков. Здесь вспоминаем, что конъюнкция – это логическая операция, которая объединяем два простых высказывания в сложное с помощью логической связки «и», и сложное высказывание будет приобретать значение «истина» тогда и только тогда, когда истины оба исходных простых высказывания. Таким образом, получаем, что нужно найти области, где и отрезок P и отрезок Q имеют место, а такая область только одна – отрезок [8,15] (красный цвет). Более подробно исследуем все отрезки прямой, чтобы учащимся было нагляднее и понятнее воспринимать материал, итак:
— на этом промежутке отрезки имеют следующие значения («равно 1» – ставим, если любая точка, взятая в этом промежутке будет принадлежат рассматриваемому отрезку, и «равно 0» – если точка не принадлежит отрезку) P=0, Q=0, следовательно, и конъюнкция этих отрезков будет также равна 0.
— P=1, Q=0, конъюнкция отрезков будет равна 0
— P=1, Q=1, конъюнкция отрезков будет равна 1 – это искомый нами отрезок (красный цвет) – рис. 2
— P=0, Q=1, конъюнкция отрезков будет равна 0
— P=0, Q=0, конъюнкция отрезков будет равна 0
Теперь аналогичным образом разберемся с дизъюнкцией этих отрезков. Опять же обратимся к определению этой логической операции – «дизъюнкцией называется логическая операция, которая в соответствии двум и более логическим высказываниям ставит новое, которое истинно тогда и только тогда, когда истинно хотя бы одно из входящих исходных высказываний». То есть другими словами, нам надо найти на координатной прямой такие промежутки, где есть хотя бы один из исходных наших отрезков, этот искомый промежуток будет [6,25] – зеленый цвет (рис. 2). Также разберем каждый из промежутков и покажем, что это действительно так:
— на этом промежутке отрезки имеют следующие P=0, Q=0, следовательно, и дизъюнкция этих отрезков будет также равна 0.
— P=1, Q=0, дизъюнкция отрезков будет равна 1 – искомый промежуток
— P=1, Q=1, дизъюнкция отрезков будет равна 1 – искомый промежуток
— P=0, Q=1, дизъюнкция отрезков будет равна 1 – искомый промежуток
— P=0, Q=0, дизъюнкция отрезков будет равна 0
Объединяя найденные промежутки, получаем что искомый отрезок, обозначающий дизъюнкцию исходных отрезков – это отрезок [6,25] – зеленый цвет (рис. 2).
После разбора данного примера, можно дать учащимся попробовать найти различные сочетания логических операций – дизъюнкции, конъюнкции и отрицания. Например, даны два отрезка P=[-4,10] и Q=[5,30]. Найти отрезок, который будет обозначать следующие логические операции: , , (можно придумать и другие различные сочетания этих логических операций).
решение (рис. 3). Для начала строим координатную прямую и отмечаем на ней отрезки, обозначающие исходные отрезки P=[-4,10] (синяя область) и Q=[5,30] (желтая область). Затем на прямой отмечаем промежутки, которые будут инверсией отрезка P (красные области). А теперь, пользуясь выше разобранным примером, смотрим, какие области будут отвечать за дизъюнкцию инверсии отрезка P и Q. Это будут промежутки и (зеленая область)
рис. 3
решение (рис. 4). Аналогично выше рассмотренному решению строим координатную прямую и отмечаем исходные отрезки. Но в отличие от предыдущего примера, сначала строим инверсию отрезка Q (красные области). Далее вспоминая, как мы искали промежутки, которые будут конъюнкцией двух отрезков, отмечаем тот промежуток, который послужит решением для нашего примера. Это будет (зеленая область) – рис. 4
рис. 4
решение (рис. 5). Решением для данного случая будут области и (10 — зеленая область
рис. 5
Когда разобраны все примеры, то у учащихся не возникнет трудностей с пониманием и решением задания №18 из экзаменационной работы единого государственного экзамена по информатике.
Приведем примеры решений нескольких заданий:
На числовой прямой даны два отрезка: P = [2,42] и Q =[22,62]. Выберите такой отрезок A, что формула
(x A) → ( (x P) → (x Q) ) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Возможные варианты ответов:
1) [3, 14] 2) [23, 32] 3) [43, 54] 4) [15, 45]
Решение (рис. 6): чтобы упростить понимание выражения, обозначим отдельные высказывания буквами — A: x А, P: x P, Q: x Q. Таким образом, получаем следующее выражение с учетом замены: → ( P →)=1. Равенство выражения 1 говорит о том, что какое бы значение переменной х мы не взяли, наше логическое выражение принимает значение 1, то есть на всей числовой прямой. Вспомним некоторые логические законы и равенства и преобразуем наше выражение: =1. В итоге получаем, что нам надо построить дизъюнкцию трех отрезков, два из которых нам известны. Их то мы и построим (рис. 7). Для начала, как и во всех выше приведенных примерах, мы должны построить инверсии отрезков P (оранжевый цвет) и Q (красный цвет). Затем из всего выражения мы можем определить промежутки дизъюнкции =1 (зеленые области рис. 7). Таким образом получаем, что у нас на координатной прямой есть «свободная» часть — . Эту часть прямой и должен перекрыть искомый отрезок А.
рис. 7
Рассмотрим варианты ответов:
[3, 14] – не подходит этот вариант, так как он не принадлежит совсем «свободной» части — (рис. 8)
рис. 8
[23, 32] – не подходит (рис. 9). Казалось бы, этот отрезок принадлежит «свободной» части — , но он не перекрывает его полностью. Остаются пустые части — [22, 23] и [32, 42]. Тем самым это не вариант решения задания.
рис. 9
[43, 54] — случай аналогичен первому варианту. Этот отрезок не входит в «свободной» часть — (рис. 10)
рис. 10
[15, 45]- этот вариант является верным ответом, так как полностью перекрывает «свободную» часть — (рис. 11), даже выходит за ее пределы, но это не противоречит определению дизъюнкции и является решением данного задания.
рис. 11
Можно бесконечно много рассматривать варианты задач на заданную тему, самое главное, я считаю, это дать понять учащимся, как найти области, которые будут являться инверсиями, конъюнкциями и дизъюнкциями отрезков и других множеств.
Задания для решений можно посмотреть на сайте Константина Полякова http://kpolyakov.narod.ru/school/ege.htm.
Литература
http://kpolyakov.narod.ru/school/ege.htm.
kopilkaurokov.ru
Разбор заданий от ФИПИ — 18 задание ЕГЭ информатика 2018
Из методических рекомендаций ФИПИ для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2016 года
Таким образом, результат выполнения экзаменационной работы в целом в 2016 г. несколько повысился по сравнению с 2015 г., но при этом сохранилось большинство особенностей, недостатков и проблем в подготовке выпускников, отмечавшихся в предыдущие годы.
Так, задание 18 повышенного уровня выполнено в среднем с показателем 20,2%, что, конечно, почти в два раза выше прошлогодних 11,3%, но все равно недостаточно. (при разбросе по вариантам от 5% до 19%). Задание, проверяющее это содержание (преобразование импликации в логических выражениях), существует в ЕГЭ с 2005 г., но начина с 2012 г. оно планомерно усложняется. До 2014 г. задание было в группе заданий с выбором ответа, его перенос в прошлом году в категорию заданий с кратким ответом в сочетании с вводом дополнительного содержания в ряде вариантов (функция поразрядной конъюнкции двоичных чисел) привел к существенному снижению результатов. Задание было разобрано в методических рекомендациях 2015 г. и в 2016 г. дано в более простой формулировке. Тем не менее, задание остается одним из самых сложных в варианте. В рекомендациях 2016 г. мы повторяем разбор задания в формулировке 2015 г. и дополнительно приводим разбор одного из заданий текущего года.
Задание 18 повышенного уровня сложности проверяет знание экзаменующимся таблицы истинности для импликации и умение осуществить преобразование импликации в сложных выражениях. В 2015 году задание в ряде вариантов заодно проверяло умение осуществить поразрядную конъюнкцию двоичных чисел. Оно вызвало у экзаменующихся серьезные затруднения.
Задание 18.1 Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110&0101 = 0100 = 4.
Для какого наименьшего неотрицательного целого числа А формула
x&25 ≠ 0 → (x&17 = 0 → x&А ≠ 0)
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Решение.
Поскольку выражения A → (B → C) и (A /\ B) → C равносильны, выражение x&25 ≠ 0 → (x&17 = 0 → x&A ≠ 0) равносильно выражению (x&25 ≠ 0 /\ x&17 = 0) → x&A ≠ 0.
Поскольку 25 = 11001 (в двоичной системе счисления), то x & 25 ≠ 0 означает, что или нулевой, или третий, или четвертый разряд в двоичной записи числа x не равен 0. Аналогично, x & 17 = 0 означает, что нулевой и четвертый разряд в двоичной записи числа x равны 0. Следовательно из (x&25 ≠ 0 /\ x&17 = 0) следует, что третий разряд в двоичной записи числа x не равен 0. Поэтому если 8&A ≠ 0, то выражение (x&25 ≠ 0 /\ x&17 = 0) → x&A ≠ 0 истинно при любом x, если же 8 & A = 0, то выражение ложно при, например, x = 8.
Наименьшее A, при котором 8&A ≠ 0 равно 8.
Ответ:8
В 2016 г. в некоторых вариантах задание 18 было в приведено в формулировке, требовавшей определения длин отрезков числовой прямой. Приведем пример задания 18 из одного из вариантов 2016 г.
Задание 18.2 На числовой прямой даны два отрезка: P = [30, 65] и Q = [10, 35]. Отрезок A таков, что формула ¬(x ∈ A) → ((x ∈ P) →¬ (x ∈ Q)) истинна при любом значении переменной x. Какова наименьшая возможная длина отрезка A?
Решение.
Для начала можно применить преобразование импликации два раза и получить выражение без импликации: ¬(x ∈ A) → ((x ∈ P) →¬ (x ∈ Q)) равносильно выражению ¬(x ∈ A) → ((x ∉ P) \/ (x ∉ Q)) (мы преобразовали импликацию в скобках и применили отрицание, заменив «принадлежит» на «не принадлежит). Аналогично это выражение равносильно (x ∈ A) \/ ((x ∉ P) \/ (x ∉ Q)). Скобки можно раскрыть, получаем (x ∈ A) \/ (x ∉ P) \/ (x ∉ Q). Для этого выражения формула истинна для всех x, не принадлежащих либо отрезку P, либо отрезку Q. Чтобы она была истинна для всей числовой прямой, требуется, чтобы отрезок A полностью покрывал пересечение отрезков P и Q. Минимальный такой отрезок [30, 35] совпадает с пересечением отрезков P и Q и имеет длину 5.
Ответ: 5
Как видно из приведенных примеров, задание не требует для своего выполнения каких-то знаний и умений, выходящих за рамки стандартных логических преобразований, но требует хорошего понимания глубокой взаимосвязи операций пересечения и объединения множеств с логическими операциями конъюнкции и дизъюнкции. Эти множества могут представлять собой отрезки на прямой или натуральные числа, имеющие те или иные цифры в двоичном разложении.
xn--23-6kca2bbonikw0av.xn--p1ai
Подготовка к ЕГЭ по информатике, задание 18
Задание 18 Каталог заданий. Логические высказывания
1. Задание 18 № 701. Для какого имени ложно высказывание:
(Первая буква имени гласная → Четвертая буква имени согласная).
1) ЕЛЕНА
2) ВАДИМ
3) АНТОН
4) ФЕДОР
Пояснение.
Импликация ложна тогда и только тогда, когда посылка истинна, а следствие ложно. В нашем случае — если первая буква имени гласная и четвертая буква гласная. Этому условию удовлетворяет имя Антон.
Примечание.
Тот же результат следует из следующих преобразований: ¬ (A → B) = ¬ (¬ A ∨ B) = A ∧ (¬ B).
Правильный ответ указан под номером 3.
2. Задание 18 № 8666. На числовой прямой даны два отрезка: P = [25; 50] и Q = [32; 47]. Укажите наибольшую возможную длину промежутка A, для которого формула
(¬ (x A) → (x P)) → ((x A) → (x Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Пояснение.
Преобразуем данное выражение:
(¬ (x A) → (x P)) → ((x A) → (x Q))
((x A) ∨ (x P)) → ((x не A) ∨ (x Q))
¬((x принадл A) ∨ (x принадл P)) ∨ ((x не принадл A) ∨ (x принадл Q))
(x не принадл A) ∧ (x не принадл P) ∨ (x принадл A) ∨ (x не принадл Q)
(x не принадл A) ∨ (x принадл Q)
Таким образом, либо x должен принадлежать Q, либо не принадлежать A. Это значит, что для достижения истинности для всех x, необходимо, чтобы A полностью содержался в Q. Тогда максимум, каким он сможет стать, это всем Q, то есть длиной 15.
3. Задание 18 № 9170. На числовой прямой даны два отрезка: P = [10, 35] и Q = [17, 48].
Укажите наибольшую возможную длину отрезка A, для которого формула
((x A) → ¬(x P)) → ((x A) → (x Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Пояснение.
Преобразуем данное выражение.
((x € A) → ¬(x принадл P)) → ((x принадл A) → (x принадл Q))
((x не принадл A) ∨ (x не принадл P)) → ((x не принадл A) ∨ (x принадл Q))
¬((x не принадл A) ∨ (x не принадл P)) ∨ ((x не принадл A) ∨ (x принадл Q))
Верно, что A ∧ B ∨ ¬A = ¬A ∨ B. Применим это здесь, получим:
(x принадл P) ∨ (x не принадл A) ∨ (x принадл Q)
То есть либо точка должна принадлежать Q, либо принадлежать P, либо не принадлежать А. Это значит, что А может покрывать все точки, которые покрывают P и Q. То есть A = P Q = [10, 35] [17, 48] = [10; 48]. |A| = 48 — 10 = 38.
4. Задание 18 № 9202. Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.
Известно, что выражение
((x A) → (x P)) ∨ (¬(x Q) → ¬(x A))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.

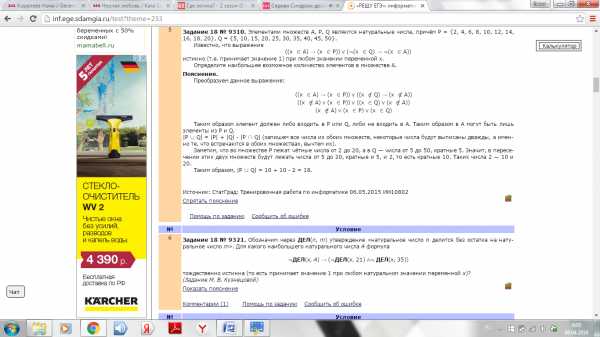
5. Задание 18 № 9310. Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50}.
Известно, что выражение
((x A) → (x P)) ∨ (¬(x Q) → ¬(x A))
истинно (т.е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.
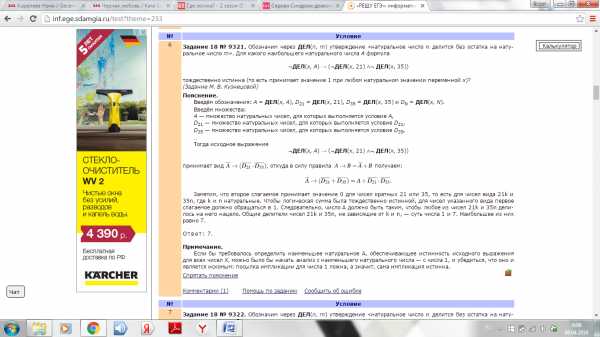
6. Задание 18 № 9321. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула
¬ДЕЛ(x, А) → (¬ДЕЛ(x, 21) ∧¬ ДЕЛ(x, 35))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменнойx)?
(Задание М. В. Кузнецовой)
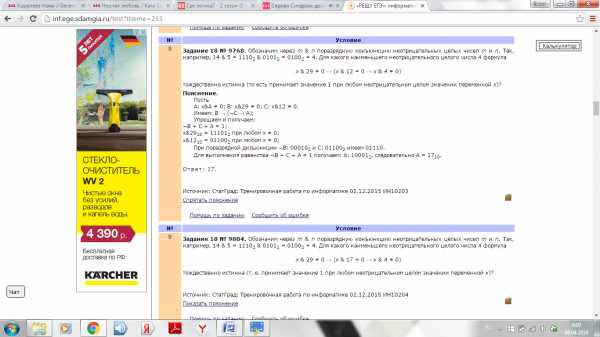
7. Задание 18 № 9768. Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 12 = 0 → x & А ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной х)?
8. Задание 18 № 9804. Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
9. Задание 18 № 723. Для какого имени истинно высказывание:
Третья буква гласная → ¬ (Первая буква согласная \/ В слове 4 гласных буквы)?
1) Римма
2) Анатолий
3) Светлана
4) Дмитрий
Пояснение.
Применим преобразование импликации:
Третья буква Согласная ∨ (Первая буква Гласная ∧ В слове НЕ 4 гласных буквы)
Дизъюнкция истинна, когда истинно хотя бы одно высказывание. Следовательно, подходит только вариант 1.
10. Задание 18 № 4581. Какое из приведённых имён удовлетворяет логическому условию:
(первая буква согласная → последняя буква согласная) /\ (первая буква гласная → последняя буква гласная)?
Если таких слов несколько, укажите самое длинное из них.
1) АННА
2) БЕЛЛА
3) АНТОН
4) БОРИС
Пояснение.
Логическое И истинно только тогда , когда истинны оба утверждения.(1)
Импликация ложна только тогда,когда из истины следует ложь.(2)
Вариант 1 подходит по всем условиям.
Вариант 2 не подходит из за условия (2).
Вариант 3 не подходит из за условия (2).
Вариант 4 подходит по всем условиям.
Необходимо указать самое длинное из слов, следовательно, ответ 4.
Задания для самостоятельного решения
1. Задание 18 № 711. Какое из приведенных названий стран удовлетворяет следующему логическому условию: ((последняя буква согласная) \/ (первая буква согласная)) → (название содержит букву «п»)?
1) Бразилия
2) Мексика
3) Аргентина
4) Куба
2. Задание 18 № 709. Какое из приведённых имен удовлетворяет логическому условию:
(Первая буква гласная) ∧ ((Четвёртая буква согласная) ∨ (B слове четыре буквы))?
1) Сергей
2) Вадим
3) Антон
4) Илья
№3
№4 
№5. Задание 18 № 736. Какое из приведённых имен удовлетворяет логическому условию
Первая буква гласная ∧ Четвёртая буква согласная ∨ В слове четыре буквы ?
1) Сергей
2) Вадим
3) Антон
4) Илья
Ответы
Числа 6,12,18
13
4
infourok.ru
