ЕГЭ математика 2018. Разбор варианта Алекса Ларина № 205
Дана правильная пирамида PABCD с вершиной в точке Р. Через точку В
перпендикулярно прямой DP проведена плоскость Ω, которая пересекает DP в точке К.
А) Докажите, что прямые ВК и АС перпендикулярны.
Б) Найдите площадь сечения пирамиды плоскостью Ω, если известно, что сторона основания пирамиды равна 6 и высота пирамиды равна 6.
а) $$BK\perp AC$$ — ?
$$BK\perp DP$$ — по условию $$\Rightarrow$$ $$KO\perp DB$$ (по построению) $$\Rightarrow$$ DB проекция KB на (ABCD) $$\Rightarrow$$, т.к. ABCD — квадрат, $$DB\perp AC$$ по теореме о трех перпендикулярах $$BK\perp AC$$
ч.т.д.
б) $$PH=6$$, $$AB=BC=6$$
Найти: $$S_{BNKL}$$ — ?
1) Введем ортогональную систему координат X0YZ.
2) $$\vec{DP}\perp (BNKL)$$ — это нормаль;
$$\vec{HP}\perp (ABCD)$$ — это нормаль; $$\Rightarrow$$
угол между (BNKL) и (ABCD)=углу между $$\vec{HD}$$ и $$\vec{DP}$$
3) $$\vec{HP}\parallel OZ$$ $$\Rightarrow$$ $$\vec{HP}\left \{ 0; 0; 6 \right \}$$
$$\left.\begin{matrix}P\left \{ 0; 0; 6 \right \}\\D\left \{ -3\sqrt{2}; 0; 0 \right \}\end{matrix}\right\}$$ $$\Rightarrow$$
$$\vec{DP}\left \{ 3\sqrt{2}; 0; 6 \right \}$$
$$\cos$$ угла между $$(\vec{HD};\vec{DP})=\frac{\left | 0\cdot3\sqrt{2}+0\cdot0+6\cdot6\right |}{\sqrt{0^{2}+0^{2}+6^{2}}\cdot\sqrt{(3\sqrt{2})^{2}+0^{2}+6^{2}}}=$$
$$=\frac{36}{6\cdot\sqrt{54}}=\frac{6}{3\sqrt{6}}=\frac{2}{\sqrt{6}}$$
4) $$\frac{S_{BCOA}}{S_{BNKL}}=\cos$$ угла между $$(\vec{HD}; \vec{DP})=\frac{2}{\sqrt{6}}$$
$$\sin$$ угла между $$(\vec{HD};\vec{DP})=\frac{\sqrt{2}}{\sqrt{6}}=\frac{\sqrt{2}}{3}=\frac{DK}{DB}$$ $$\Rightarrow$$ $$DK=DB\cdot \frac{\sqrt{3}}{3}=\frac{\sqrt{3}}{3}\cdot 6\sqrt{2}=2\sqrt{6}$$
5) $$\sin$$ угла между $$(\vec{HD}; \vec{DP})=\cos KDO=\frac{\sqrt{3}}{3}$$ $$\Rightarrow$$ $$DO=DK\cdot \cos KDO=2\sqrt{6}\cdot \frac{\sqrt{3}}{3}=2\sqrt{2}$$ $$\Rightarrow$$ $$OH=\sqrt{2}$$; $$BO=4\sqrt{2}$$
6) $$KO=4$$ $$\bigtriangleup KOB\sim \bigtriangleup JHB$$ $$\Rightarrow$$ $$\frac{KO}{JH}=\frac{OB}{HB}$$ $$\Rightarrow$$ $$JH=3$$ $$\Rightarrow$$ $$JH=\frac{1}{2}PH$$ $$\Rightarrow$$ $$LN=\frac{1}{2}AC=3\sqrt{2}$$
$$KB=\sqrt{KO^{2}+OB^{2}}=4\sqrt{3}$$
$$S_{BNKL}=\frac{1}{2}KB\cdot LN=\frac{1}{2}\cdot 4\sqrt{3}\cdot 3\sqrt{2}=6\sqrt{6}$$
mathlesson.ru
239 вариант Алекса Ларина. Разбор ЕГЭ математика 2018.
Найдите все значения параметра а, при каждом из которых уравнение $$(|2x+1-a|+|2x+1+a|-2a)(|x^{2}-2x+a|+|x^{2}-2x-a|-2a)=0 $$имеет ровно четыре целых решения
Рассмотрим каждую скобку по отдельности. Так как произведение равно нулю, когда один из множителей равно нулю, то итоговым решением будет совокупность решений каждой скобки:
Пусть : $$|2x+1-a|+|2x+1+a|-2a=0 (A)$$ или $$|x^{2}-2x+a|+|x^{2}-2x-a|-2a=0 (B)$$
A) Раскроем модули. Модули равны 0, если $$2x+1=\pm a$$. Отметим данные значения на координатной прямой, рассмотрим, какие знаки принимают подмодульные выражения:
1)Если $$2x+1 < -a \Leftrightarrow$$$$a < -2x -1$$. Тогда : $$-2x-1+a-2x-1-a-2a=0 \Leftrightarrow$$$$a=-2x-1$$. Но данное уравнение не имеет решения в силу строгости условия раскрытия модуля
2)Если $$-a \leq 2x+1 \leq a \Leftrightarrow $$$$\left\{\begin{matrix}a \geq -2x-1\\a\geq 2x+1 \end{matrix}\right.$$. Тогда $$-2x-1+a+2x+1+a-2a=0 \Leftrightarrow$$$$0=0$$. Получили верное числовое равенство, следовательно решением будет любая точка, удовлетворяющая условию раскрытия модуля. Найдем область этих точек. Для этого строится график каждой функции поочередно, он разбивает координатную плоскость на две полуплоскости. Берется любая точка из любой полуплоскости и проверяется на выполнение неравенства, если оно выполняется, то полуплоскость является решением, если нет — то решением является другая полуплоскость. Рассмотрим на примере $$a \geq -2x-1$$. Начертим график функции $$a =-2x-1$$. Возьмем точку, не принадлежащую графики, например (0;0) и проверим выполнение неравенства:$$0 \geq -2*0 — 1 \Leftrightarrow$$$$0\geq -1$$ — неравенство верное, следовательно, полуплоскость, где лежит эта точка является решением ( на рисунке бежевым ). Для второго неравенства решение черным. Решением же системы является пересечение областей (темно-бежевый)
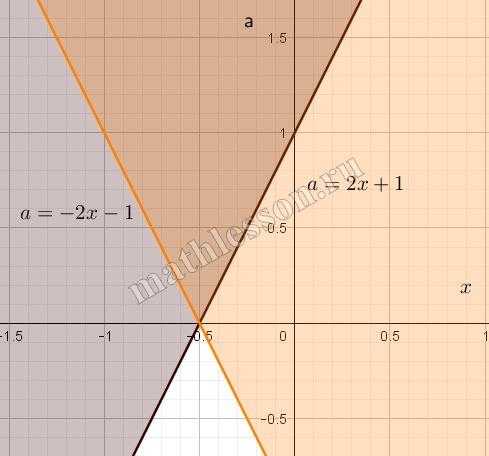
3)Если $$a > 2x+1$$. Тогда: $$2x+1-a+2x+1+a-2a=0 \Leftrightarrow$$$$a=2x+1$$. Данное уравнение не имеет решений в силу строгости условия раскрытия модуля.
Б)Раскроем модули. Модули равны 0, если $$x^{2}-2x=\pm a$$. Отметим данные значения на координатной прямой, рассмотрим, какие знаки принимают подмодульные выражения:
1)Если $$x^{2}-2x < -a \Leftrightarrow$$$$a < x^{2}-2x$$. Тогда : $$-x^{2}+2x-a-x^{2}+2x+a-2a=0 \Leftrightarrow$$$$a=-x^{2}+2x$$. Но данное уравнение не имеет решения в силу строгости условия раскрытия модуля
2)Если $$-a \leq x^{2}-2x \leq a \Leftrightarrow $$$$\left\{\begin{matrix}a \geq -x^{2}+2x\\ a\geq x^{2}-2x \end{matrix}\right.$$. Тогда $$x^{2}-2x+a-x^{2}+2x+a-2a=0 \Leftrightarrow$$$$0=0$$. Получили верное числовое равенство, следовательно решением будет любая точка, удовлетворяющая условию раскрытия модуля. Найдем область этих точек. Для первого неравенства область чертного цвета, для второго — бежевого, для системы же — темно-бежевый
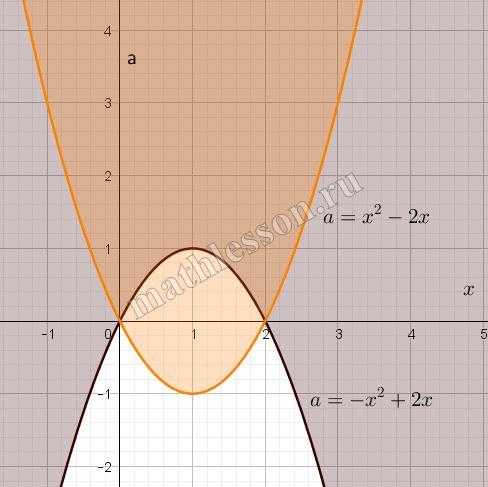
3)Если $$a > x^{2}-2x$$. Тогда: $$x^{2}-2x+a+x^{2}-2x-a-2a=0 \Leftrightarrow$$$$a=x^{2}-2x$$. Данное уравнение не имеет решений в силу строгости условия раскрытия модуля.
Итоговой областью решения будет множество точек объединения получившихся промежутков (фиолетовая область):
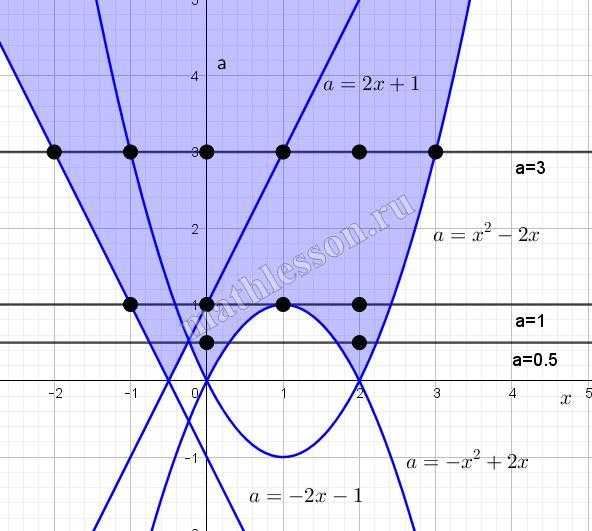
Наим необходимо, чтобы было ровно 4 целых значения х. Построим прямую $$a=0,5$$ Как видим, целых абсцисс, попавших в пересечение прямой и области решения всего 2 ( 0 и 2). Построим прямую $$a=1$$. Как видим, целых абсцисс получаем 4 (-1 ; 0 ; 1 ; 2). Построим прямую $$a=3$$, там уже будет 6 целых абсцисс (-2 ; -1 ; 0 ; 1 ; 2 ; 3). Следовательно, решением будет $$a \in [1 ; 3)$$
mathlesson.ru
Решения ЕГЭ alexlarin.net | ЕГЭ решебник
Здесь представлены решения тренировочных вариантов ЕГЭ с сайта alexlarin.net, публикуемые еженедельно каждую субботу.
Решение задач тренировочного варианта 248
вариант от 03 ноября 2018 г.
Решение задач тренировочного варианта 247
вариант от 27 октября 2018 г.
Решение задач тренировочного варианта 246
вариант от 20 октября 2018 г.
Решение задач тренировочного варианта 245
вариант от 13 октября 2018 г.
Решение задач тренировочного варианта 244
вариант от 06 октября 2018 г.
Решение задач тренировочного варианта 243
вариант от 29 сентября 2018 г.
Решение задач тренировочного варианта 242
вариант от 22 сентября 2018 г.
Решение задач тренировочного варианта 241
вариант от 15 сентября 2018 г.
Решение задач тренировочного варианта 240
вариант от 08 сентября 2018 г.
Решение задач тренировочного варианта 238
вариант от 19 мая 2018 г.
Решение задач тренировочного варианта 237
вариант от 12 мая 2018 г.
Решение задач тренировочного варианта 236
вариант от 05 мая 2018 г.
Решение задач тренировочного варианта 235
вариант от 28 апреля 2018 г.
Решение задач тренировочного варианта 234
вариант от 21 апреля 2018 г.
Решение задач тренировочного варианта 233
вариант от 14 апреля 2018 г.
Решение задач тренировочного варианта 232
вариант от 07 апреля 2018 г.
Решение задач тренировочного варианта 231
вариант от 31 марта 2018 г.
Решение задач тренировочного варианта 230
вариант от 24 марта 2018 г.
Решение задач тренировочного варианта 229
вариант от 17 марта 2018 г.
Решение задач тренировочного варианта 228
вариант от 10 марта 2018 г.
Решение задач тренировочного варианта 227
вариант от 03 марта 2018 г.
Решение задач тренировочного варианта 226
вариант от 24 февраля 2018 г.
Решение задач тренировочного варианта 225
вариант от 17 февраля 2018 г.
Решение задач тренировочного варианта 224
вариант от 10 февраля 2018 г.
Решение задач тренировочного варианта 223
Решение задач тренировочного варианта 222
вариант от 27 января 2018 г.
Решение задач тренировочного варианта 221
вариант от 20 января 2018 г.
Решение задач тренировочного варианта 220
вариант от 13 января 2018 г.
Решение задач тренировочного варианта 219
вариант от 06 января 2018 г.
Решение задач тренировочного варианта 218
вариант от 30 декабря 2017 г.
Решение задач тренировочного варианта 217
вариант от 23 декабря 2017 г.
Решение задач тренировочного варианта 216
вариант от 16 декабря 2017 г.
Решение задач тренировочного варианта 215
вариант от 09 декабря 2017 г.
Решение задач тренировочного варианта 214
вариант от 02 декабря 2017 г.
Решение задач тренировочного варианта 213
вариант от 25 ноября 2017 г.
Решение задач тренировочного варианта 212
вариант от 18 ноября 2017 г.
Решение задач тренировочного варианта 211
вариант от 11 ноября 2017 г.
Решение задач тренировочного варианта 210
вариант от 04 ноября 2017 г.
Решение задач тренировочного варианта 209
вариант от 28 октября 2017 г.
Решение задач тренировочного варианта 208
вариант от 21 октября 2017 г.
Решение задач тренировочного варианта 207
вариант от 14 октября 2017 г.
Решение задач тренировочного варианта 206
вариант от 07 октября 2017 г.
Решение задач тренировочного варианта 205
вариант от 30 сентября 2017 г.
Решение задач тренировочного варианта 204
вариант от 23 сентября 2017 г.
Решение задач тренировочного варианта 203
вариант от 16 сентября 2017 г.
Решение задач тренировочного варианта 202
вариант от 09 сентября 2017 г.
Решение задач тренировочного варианта 201
вариант от 02 сентября 2017 г.
Решение задач тренировочного варианта 200
вариант от 29 мая 2017 г.
Решение задач тренировочного варианта 199
вариант от 25 мая 2017 г.
Решение задач тренировочного варианта 198
вариант от 20 мая 2017 г.
Решение задач тренировочного варианта 197
вариант от 13 мая 2017 г.
Решение задач тренировочного варианта 196
вариант от 06 мая 2017 г.
Решение задач тренировочного варианта 195
вариант от 29 апреля 2017 г.
Решение задач тренировочного варианта 194
вариант от 22 апреля 2017 г.
Решение задач тренировочного варианта 193
вариант от 15 апреля 2017 г.
Решение задач тренировочного варианта 192
вариант от 08 апреля 2017 г.
Решение задач тренировочного варианта 191
вариант от 01 апреля 2017 г.
Решение задач тренировочного варианта 190
вариант от 25 марта 2017 г.
Решение задач тренировочного варианта 189
вариант от 18 марта 2017 г.
Решение задач тренировочного варианта 188
вариант от 10 марта 2017 г.
Решение задач тренировочного варианта 187
вариант от 03 марта 2017 г.
Решение задач тренировочного варианта 186
вариант от 25 февраля 2017 г.
Решение задач тренировочного варианта 185
вариант от 18 февраля 2017 г.
Решение задач тренировочного варианта 184
вариант от 11 февраля 2017 г.
Решение задач тренировочного варианта 183
вариант от 04 февраля 2017 г.
Решение задач тренировочного варианта 182
вариант от 28 января 2017 г.
Решение задач тренировочного варианта 181
вариант от 21 января 2017 г.
Решение задач тренировочного варианта 180
вариант от 14 января 2017 г.
Решение задач тренировочного варианта 179
вариант от 07 января 2017 г.
Решение задач тренировочного варианта 178
вариант от 31 декабря 2016 г.
Решение задач тренировочного варианта 177
вариант от 24 декабря 2016 г.
Решение задач тренировочного варианта 176
Решение задач тренировочного варианта 175
вариант от 10 декабря 2016 г.
Решение задач тренировочного варианта 174
вариант от 03 декабря 2016 г.
Решение задач тренировочного варианта 173
вариант от 26 ноября 2016 г.
Решение задач тренировочного варианта 172
вариант от 19 ноября 2016 г.
Решение задач тренировочного варианта 171
вариант от 12 ноября 2016 г.
Решение задач тренировочного варианта 170
вариант от 05 ноября 2016 г.
Решение задач тренировочного варианта 169
вариант от 29 октября 2016 г.
Решение задач тренировочного варианта 168
вариант от 22 октября 2016 г.
Решение задач тренировочного варианта 167
вариант от 15 октября 2016 г.
Решение задач тренировочного варианта 166
вариант от 08 октября 2016 г.
Решение задач тренировочного варианта 165
вариант от 01 октября 2016 г.
Решение задач тренировочного варианта 164
вариант от 24 сентября 2016 г.
Решение задач тренировочного варианта 163
вариант от 17 сентября 2016 г.
Решение задач тренировочного варианта 162
вариант от 10 сентября 2016 г.
Решение задач тренировочного варианта 161
вариант от 03 сентября 2016 г.
Решение задач тренировочного варианта 160
вариант от 04 июня 2016 г.
Решение задач тренировочного варианта 159
вариант от 28 мая 2016 г.
Решение задач тренировочного варианта 158
вариант от 21 мая 2016 г.
Решение задач тренировочного варианта 157
вариант от 14 мая 2016 г.
Решение задач тренировочного варианта 156
вариант от 07 мая 2016 г.
Решение задач тренировочного варианта 155
вариант от 30 апреля 2016 г.
Решение задач тренировочного варианта 154
вариант от 23 апреля 2016 г.
Решение задач тренировочного варианта 153
вариант от 16 апреля 2016 г.
Решение задач тренировочного варианта 152
вариант от 09 апреля 2016 г.
Решение задач тренировочного варианта 151
вариант от 02 апреля 2016 г.
Решение задач из досрочного образца ЕГЭ от 28 марта 2016
вариант от 28 марта 2016 г.
Решение задач тренировочного варианта 150
вариант от 26 марта 2016 г.
Решение задач тренировочного варианта 149
вариант от 19 марта 2016 г.
Решение задач тренировочного варианта 148
вариант от 12 марта 2016 г.
Решение задач тренировочного варианта 147
вариант от 05 марта 2016 г.
Решение задач тренировочного варианта 146
вариант от 27 февраля 2016 г.
Решение задач тренировочного варианта 145
вариант от 20 февраля 2016 г.
Решение задач тренировочного варианта 144
вариант от 13 февраля 2016 г.
Решение задач тренировочного варианта 143
вариант от 06 февраля 2016 г.
Решение задач тренировочного варианта 142
вариант от 30 января 2016 г.
Решение задач тренировочного варианта 141
вариант от 23 января 2016 г.
Решение задач тренировочного варианта 140
вариант от 16 января 2016 г.
Решение задач тренировочного варианта 139
вариант от 09 января 2016 г.
Решение задач тренировочного варианта 138
вариант от 02 января 2016 г.
Решение задач тренировочного варианта 137
вариант от 26 декабря 2015 г.
Решение задач тренировочного варианта 136
вариант от 19 декабря 2015 г.
Решение задач тренировочного варианта 135
вариант от 12 декабря 2015 г.
Решение задач тренировочного варианта 134
вариант от 05 декабря 2015 г.
Решение задач тренировочного варианта 133
вариант от 28 ноября 2015 г.
Решение задач тренировочного варианта 132
вариант от 21 ноября 2015 г.
Решение задач тренировочного варианта 131
вариант от 14 ноября 2015 г.
Решение задач тренировочного варианта 130
вариант от 07 ноября 2015 г.
Решение задач тренировочного варианта 129
вариант от 31 октября 2015 г.
Решение задач тренировочного варианта 128
вариант от 24 октября 2015 г.
Решение задач тренировочного варианта 127
вариант от 17 октября 2015 г.
Решение задач тренировочного варианта 126
вариант от 10 октября 2015 г.
Решение задач тренировочного варианта 125
вариант от 03 октября 2015 г.
Решение задач тренировочного варианта 124
вариант от 26 сентября 2015 г.
Решение задач тренировочного варианта 123
вариант от 19 сентября 2015 г.
Решение задач тренировочного варианта 122
вариант от 12 сентября 2015 г.
Решение задач тренировочного варианта 121
вариант от 05 сентября 2015 г.
Решение задач тренировочного варианта 120
вариант от 30 мая 2015 г.
Решение задач тренировочного варианта 119
вариант от 23 мая 2015 г.
Решение задач тренировочного варианта 118
вариант от 16 мая 2015 г.
Решение задач тренировочного варианта 117
вариант от 09 мая 2015 г.
Решение задач тренировочного варианта 116
вариант от 02 мая 2015 г.
Решение задач тренировочного варианта 115
вариант от 25 апреля 2015 г.
Решение задач тренировочного варианта 114
вариант от 18 апреля 2015 г.
Решение задач тренировочного варианта 113
вариант от 11 апреля 2015 г.
Решение задач из досрочного варианта ЕГЭ от 26 марта 2015 г.
вариант от 26 марта 2015 г.
Решение задач тренировочного варианта 112
вариант от 04 апреля 2015 г.
Решение задач тренировочного варианта 111
вариант от 28 марта 2015 г.
Решение задач тренировочного варианта 110
вариант от 21 марта 2015 г.
Решение задач тренировочного варианта 109
вариант от 14 марта 2015 г.
Решение задач тренировочного варианта 108
вариант от 07 марта 2015 г.
Решение задач тренировочного варианта 107
вариант от 28 февраля 2015 г.
Решения задач тренировочного варианта 106
вариант от 21 февраля 2015 г.
Решения задач тренировочного варианта 105
вариант от14 февраля 2015 г.
Решения задач тренировочного варианта 104
вариант от 07 февраля 2015 г.
ege4.me
244 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Найти все значения параметра $$\pi<\alpha<\pi$$ , $$\left\{\begin{matrix}(4-x^{2}-y^{2})(y^{2}-4x+28)=0 \\x \cos \alpha +y \sin \alpha =2\end{matrix}\right.$$ при которых система уравнений имеет ровно три решения.
$$\left\{\begin{matrix}(4-x^{2}-y^{2})(y^{2}-4x+28)=0 \\x \cos \alpha +y \sin \alpha =2\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}x^{2}+y^{2}=4\\x \cos \alpha +y \sin \alpha =2 (1)\end{matrix}\right.\\\left\{\begin{matrix}y^{2}-4x+8-0\\x \cos \alpha +y \sin \alpha =2 (2)\end{matrix}\right.\end{matrix}\right.$$
Рассмотрим систему (1) :
$$x \cos \alpha +y \sin \alpha =2\Leftrightarrow y=\frac{-x \cos \alpha +2}{\sin \alpha }=-ctg \alpha *x+\frac{2}{\sin \alpha }$$. Построим данную прямую . Она смешена по Oy на $$\frac{2}{\sin \alpha }$$

Пусть $$\angle OAB=\alpha$$, тогда $$\angle BCO=90-\alpha$$ , и смежный с ним $$\alpha -90$$. Для прямой $$y=kx+b; k=tg \beta$$ ,где $$\beta$$-угол между прямой и Ox: $$tg(\alpha -90)=-ctg \alpha$$
Длина OB из $$\Delta ABO: OA*\sin \alpha =\frac{2}{\sin \alpha }*\sin\alpha =2$$ Т.е. независимо от $$\alpha$$ , длина OB всегда что составляет радиус окружности $$x^{2}+y^{2}=4$$. Т.е. $$y=-ctg \alpha *x+\frac{2}{\sin \alpha }$$ при всех $$\alpha$$ — касательная ,следовательно, одно решения есть.
Рассмотрим систему (2):она должна иметь ровно 2 решения :
$$\left\{\begin{matrix} y^{2}-4x+28=0 & & \\ x \cos \alpha +y \sin \alpha =2 & & \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} y^{2}-4*\frac{2-y \sin \alpha }{\cos ^{2}}+28=0 & & \\ x=\frac{2-y\sin \alpha }{\cos x}& & \end{matrix}\right.$$
Учитываем ,что: $$\cos \alpha \neq 0\Leftrightarrow \alpha \neq \frac{\pi}{2}+\pi n , n \in Z$$
$$y^{2}-*\frac{4*(2-y \sin\alpha )}{\cos \alpha }+28=0$$
$$y^{2}\cos \alpha -8+4y \sin \alpha +28 \cos \alpha =0$$
Чтобы было два решения, дискриминант должен быть строго больше 0:
$$D=(4 \sin \alpha )^{2}-4 \cos \alpha (28 \cos \alpha -8)>0$$
$$16 \sin^{2}\alpha -16 \cos\alpha (7\cos\alpha -2)>0$$
$$\sin^{2}-7\cos^{2}\alpha +2\cos\alpha >0$$
$$1-\cos^{2}\alpha -7 \cos ^{2}\alpha +2 \cos \alpha >0$$
$$8 \cos^{2}-2 \cos \alpha -1<0$$
$$D=4+32=36$$
$$\cos \alpha =\frac{2+6}{16}=\frac{1}{2}$$ и $$\cos \alpha =\frac{2-6}{16}$$
Получаем: $$\left\{\begin{matrix}\cos \alpha >-\frac{1}{4} & & \\\cos \alpha <\frac{1}{2} & &\end{matrix}\right.$$. Учтем ,что $$\alpha \in (-\pi; \pi) \alpha \neq \frac{\pi}{2}+\pi n$$
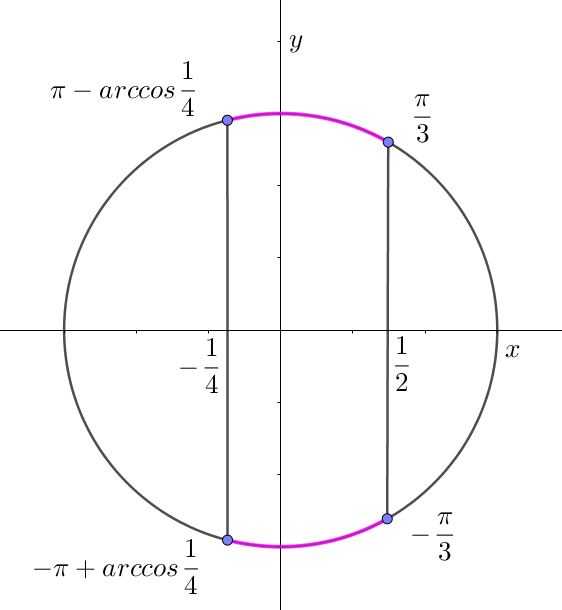
$$\alpha \in (-\pi +\arccos\frac{1}{4}; -\frac{\pi}{2})\cup (-\frac{\pi}{2};-\frac{\pi}{3})\cup (\frac{\pi}{3};\frac{\pi}{2})\cup (\frac{\pi}{2} ;\pi-\arccos \frac{1}{4})$$
mathlesson.ru
241 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Найдите все значения параметра a , при каждом из которых уравнение $$a^{2}+8|x-5|+2\sqrt{x^{2}-10x+29}=2a+|x-2a-5|$$ имеет хотя бы один корень.
$$a ^{2}+8\left | x-5 \right |+2\sqrt{x^{2}-10x+29}=2a +\left | x-2a -5 \right |$$
Пусть x-5=y
$$a ^{2}+8\left | y \right |+2\sqrt{y^{2}+4}=2a +\left | y-2a \right |$$
$$2\sqrt{y^{2}+4}= 2a -a ^{2}-8\left | y \right |+\left | y-2a \right |$$
Рассмотрим обе части уравнения как отдельные функции g(y) и f(y):
$$g(y)=2\sqrt{y^{2}+4}$$ — график данной функции — ветви параболы
При этом минимальное значение будет: $$g_{min}=g(0)=2\sqrt{0+4}=4$$
Рассмотрим функцию f(y): так как там есть модуль и параметр, то будет несколько вариантов раскрытия:
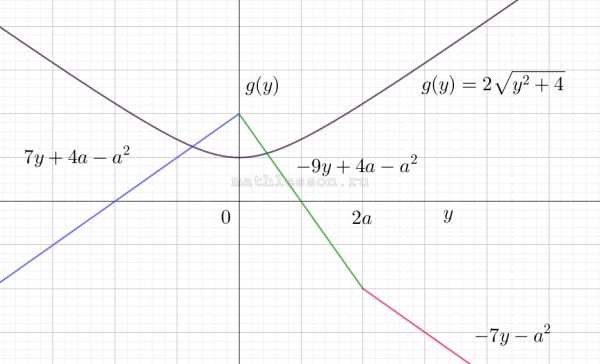
$$f(g)=2a -a ^{2}-8\left | y \right |+\left | y-2a \right |$$ — кусочно-линейная функция
а)Пусть $$2a \geq 0$$, тогда
1)$$y\leq 0$$ $$f(y)=2a -a ^{2}+8y-y+2a =7y+4a -a ^{2}$$ — синий цвет
2)$$y\in (0 ; 2a )$$ $$f(y)=2a -a ^{2}-8y-y+2a =-9y+4a -a ^{2}$$ — зеленый цвет
3) $$y> 2a$$ $$f(y)=2a -a ^{2}-8y+y-2a =-7y-a ^{2}$$ — красный цвет
Схематичное изображение графика:

Как видим максимальное значение в координате $$y=0$$: $$f_{max}=f(0)=2a =a ^{2}+\left | -2a \right |$$
б)Пусть $$2a < 0$$
1)$$y\leq 2a$$ $$f(y)=2a -a ^{2}+8y-y+2a =7y+4a -a ^{2}$$
2)$$y\in (2a; 0)$$ $$f(y)=2a -a ^{2}+8y+y-2a =9y-a ^{2}$$
3)$$y\geq 2a$$ $$f(y)=2a -a ^{2}-8y+y-2a =-7y-a ^{2}$$
Схематичное изображение графика:

И тут максимальное значение в координате $$y=0$$: $$f_{max}=f(0)$$. То есть, независимо от значения $$a$$ максимальное значение при $$y=0$$.
Тогда , чтобы были решения $$g_{min}\leq f_{max}$$ (графическая интерпритация):
Тогда:
$$4\leq 2a -a ^{2}+\left | -2a \right |\Leftrightarrow$$$$a ^{2}-2a -\left |- 2a \right | +4\leq 0$$
Расскроем модуль:
1)$$-2a \geq 0\Rightarrow a \leq 0$$. Тогда $$a ^{2}-2a +2a +4\leq 0\Rightarrow a ^{2}+4\leq 0\Rightarrow$$ решений нет
2) $$-2a < 0\Rightarrow a > 0$$. Тогда $$a ^{2}-2a -2a +4\leq 0\Rightarrow (a -2)^{2}\leq 0\Rightarrow a =2$$
mathlesson.ru
| Форум | Темы | Сообщений | Последнее сообщение | |
|---|---|---|---|---|
| Общие вопросы | 601 |
11540 |
06 ноя 2018, 22:17 сергей королев |
|
|
Решение задач
Форум для решений и обсуждений |
3071 |
27349 |
47 минут назад alex123 |
|
|
Подготовка к ЕГЭ
Задачи для подготовки к ЕГЭ |
2428 |
68128 |
Вчера, 14:19 Overk |
|
| Варианты ЕГЭ | 236 |
9388 |
01 июн 2018, 20:28 OlG |
|
| Полезная информация | 158 |
1656 |
07 ноя 2018, 12:50 serg_l |
|
|
Интересные задачки
Для желающих порешать и обменяться мнениями |
549 |
6235 |
29 сен 2018, 22:44 OlG |
|
|
Геометрия
Здесь все геометрические задачи |
1342 |
7674 |
06 ноя 2018, 18:04 vyv2 |
|
| Компьютерные программы по математике | 93 |
2440 |
09 сен 2018, 15:11 sosna24k |
|
|
ЕГЭ
Сам экзамен |
165 |
6788 |
20 сен 2018, 09:03 Мария2105 |
|
|
ГИА-9
Все о ГИА |
324 |
12618 |
Вчера, 21:36 Юлия 68 |
|
| Олимпиады | 208 |
1952 |
08 окт 2018, 22:16 Echo |
|
| Онлайн-турниры | 54 |
2559 |
07 сен 2014, 09:29 admin |
|
|
Физика
Форум для подготовки к физике (К.О.) Модераторы: eduhelper, Serpuhov |
1378 |
15148 |
03 ноя 2018, 12:24 gsnn |
|
|
Видео (сюжеты, учебные фильмы, лекции) по математике
Интересные факты, история математики. Модератор: Сан Саныч |
37 |
527 |
11 май 2018, 21:09 VICTORSH |
|
|
Разное
Сплетни, новости, общение на любые темы |
308 |
6019 |
Вчера, 17:01 OlG |
|
alexlarin.com
| Форум | Темы | Сообщений | Последнее сообщение | |
|---|---|---|---|---|
| Общие вопросы | 601 |
11540 |
06 ноя 2018, 22:17 сергей королев |
|
|
Решение задач
Форум для решений и обсуждений |
3071 |
27349 |
47 минут назад alex123 |
|
|
Подготовка к ЕГЭ
Задачи для подготовки к ЕГЭ |
2428 |
68128 |
Вчера, 14:19 Overk |
|
| Варианты ЕГЭ | 236 |
9388 |
01 июн 2018, 20:28 OlG |
|
| Полезная информация | 158 |
1656 |
07 ноя 2018, 12:50 serg_l |
|
|
Интересные задачки
Для желающих порешать и обменяться мнениями |
549 |
6235 |
29 сен 2018, 22:44 OlG |
|
|
Геометрия
Здесь все геометрические задачи |
1342 |
7674 |
06 ноя 2018, 18:04 vyv2 |
|
| Компьютерные программы по математике | 93 |
2440 |
09 сен 2018, 15:11 sosna24k |
|
|
ЕГЭ
Сам экзамен |
165 |
6788 |
20 сен 2018, 09:03 Мария2105 |
|
|
ГИА-9
Все о ГИА |
324 |
12618 |
Вчера, 21:36 Юлия 68 |
|
| Олимпиады | 208 |
1952 |
08 окт 2018, 22:16 Echo |
|
| Онлайн-турниры | 54 |
2559 |
07 сен 2014, 09:29 admin |
|
|
Физика
Форум для подготовки к физике (К.О.) Модераторы: eduhelper, Serpuhov |
1378 |
15148 |
03 ноя 2018, 12:24 gsnn |
|
|
Видео (сюжеты, учебные фильмы, лекции) по математике
Интересные факты, история математики. Модератор: Сан Саныч |
37 |
527 |
11 май 2018, 21:09 VICTORSH |
|
|
Разное
Сплетни, новости, общение на любые темы |
308 |
6019 |
Вчера, 17:01 OlG |
|
alexlarin.com
