18 информатика егэ – Презентация решения задачи №18 ЕГЭ по информатике 11 класс (логика и множества)

Разбор 18 задания ЕГЭ 2017 по информатике из демоверсии

Разбор 18 задания ЕГЭ 2017 года по информатике из проекта демоверсии. Это задание повышенного уровня сложности. Примерное время выполнения задания 3 минуты.

Проверяемые элементы содержания:
— знание основных понятий и законов математической логики.

Элементы содержания, проверяемые на ЕГЭ:
— высказывания, логические операции, кванторы, истинность высказывания.

Задание 18

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110₂&0101₂ = 0100₂ = 4.

Для какого наименьшего неотрицательного целого числа А формула

x&51 = 0 ∨ (x&41 = 0 → x&А ≠ 0)

тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Ответ: ________

Разбор 18 задания ЕГЭ 2017

1) Для начала упростим нашу формулу x&51 = 0 ∨ (x&41 = 0 → x&А ≠ 0)

, заменив импликацию простыми логическими операциями используя формулу: A→B = ¬A + B

x&51 = 0 ∨ x&41 ≠ 0 ∨ x&А ≠ 0

2) Рассмотрим первое выражение (x&51 = 0) и узнаем для каких чисел X это выражение будет истинно:
Переведём число 51 в двоичную систему счисления

51₁₀ = 110011₂

3) Определяем те значения X, при которых истинно выражение x&51 = 0:
51₁₀ 110011
  Х    111111
=0    110011

Если в числе Х на месте 1-го, 2-го, 5-го и 6-го разряда окажутся единицы, то после поразрядной конъюнкции на этих местах также будут стоять единицы, т.е. мы не получим «0» и выражение (x&51 = 0) будет ЛОЖНО.
Все остальные цифры в числе X могут быть любыми, так как после поразрядной конъюнкции на этих местах все равно будет «0».

Значит первое слагаемое учитывает все числа х, в которых нет на 1-м, 2-м, 5-м и 6-м местах единиц.

4) Рассмотрим второе выражение (x&41 ≠ 0): только для тех чисел Х, у которых на 1-м, 2-м, 5-м и 6-м местах стоят единицы.
Переведём число 41 в двоичную систему счисления

41₁₀ = 101001₂

5) Определяем те значения X, при которых истинно выражение x&41 ≠ 0:
41₁₀ 101001
  Х    11    11
≠0    10    01

Если в числе Х на месте 2-го и 5-го разряда стоят единицы, то после поразрядной конъюнкции на этих местах будут стоять нули, т.е. мы не получим «1» и выражение (x&41 ≠ 0) будет ложно.
Единицы на 1-м и 6-м месте в числе Х после поразрядной конъюнкции дадут «1» и выражение

(x&41 ≠ 0) будет истинно.
Значит второе слагаемое учитывает числа Х, в которых на 1-м и 6-м местах стоят «1» и не учитывает числа Х, в которых на 2-м и 5-м местах стоят «1».

6) Рассмотрим третье выражение (x&A≠0):
У нас остались неучтенными лишь те числа Х, у которых на 5-м и 2-м месте стоят «1», следовательно, их нужно учесть в числе А.
Минимально возможное такое число это 10010₂ = 18₁₀

Ответ: 18

infedu.ru

Разбор 18 задания ЕГЭ 2016 по информатике

Разбор 18 задания ЕГЭ 2016 года по информатике из демоверсии. Это задание на знание основных понятий и законов математической логики (уметь вычислять логическое значение сложного высказывания по известным значениям элементарных высказываний). Это задание повышенного уровня сложности. Примерное время выполнения задания 3 минуты.

Задание 18:

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110₂&0101₂ = 0100₂ = 4.

Для какого наименьшего неотрицательного целого числа А формула

x&25 ≠ 0 → (x&17 = 0 → x&А ≠ 0)

тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Ответ: ________

Разбор 18 задания ЕГЭ 2016:

Преобразуем исходное выражение

x&25 ≠ 0 → (x&17 = 0 → x&А ≠ 0)
¬(x&25 ≠ 0) ∨ (¬(x&17 = 0) ∨ x&А ≠ 0)

x&25 = 0 ∨ x&17 ≠ 0 ∨ x&А ≠ 0

Переведем числа из выражения в двоичную систему счисления

25₁₀ = 11001₂
17₁₀ = 10001₂

Определяем те значения Х, при которых истинно выражение

x&25 = 0

25₁₀ 11001
  Х    00??0
  0    00000

Х — 00??0

Определяем те значения Х, при которых истинно выражение x&17 ≠ 0

17₁₀ 10001
  Х    ?????
  0    ?000?

Х — 1????, ????1, 1???1

Следовательно

Х — 01??0

Определим наименьшее А, при котором истинно выражение x&А ≠ 0
Х — 01??0

А₁₀ ?????
 Х   01??0
≠ 0  0???0

Очевидно, что А ≠ 0

Пусть А = 1₂

А₁₀ ????1
 Х   01??0
≠ 0  00000

не подходит, так как не выполняется условие А ≠ 0

Пусть А = 1000₂

А₁₀ 01000
 Х   01??0
≠ 0  01000

подходит, 1000₂ = 8₁₀

Ответ: 8

infedu.ru

Задача 18 — разбор задания ЕГЭ по предмету Информатика

Решение №2

Можно предложить несколько более короткий подход. Обозначим наше высказывание как F = (A->(B->C)), где А — это высказывание «Х&25 не равно 0», В= «Х&17=0″ и C=»X&A не равно 0».

Раскроем импликации, пользуясь известным законом X->Y = не(Х) ИЛИ Y, получим F = A -> (не(В) ИЛИ C) = не(А) ИЛИ не(B) ИЛИ С. Распишем также двоичные значения констант 25 и 17:

25 = 11001

17 = 10001

Наше выражение — логическое ИЛИ от трёх высказываний:

1) не(А) — это значит, X&25 = 0 (биты 0,3,4 числа Х все равны 0)

2) не(B) — значит, X&17 не равно 0 (биты 0 и 4 числа Х хотя бы один равен 1)

3) C — знаит, X&A не равно 0 (биты, задаваемые маской A, хотя бы 1 равен 1)

Х  — произвольное число. Все его биты независимы. Поэтому требовать выполнения какого-то условия на биты произвольного числа можно только в одном единственном случае — когда речь идёт об одной и той же маске (наборе битов). Мы можем заметить, что двоичная маска 17 — почти то же самое, что и 25, только не хватает бита номер 3. Вот если бы дополнить 17 битом номер 3, то выражение (не(В) ИЛИ С) превратилось бы в не(неА), т.е. в А = (X&25 не равно 0). По-другому: допустим, А=8 (бит 3=1). Тогда требование (не(В) B или С) равносильно требованию: (Хотя бы один из битов 4,0 равен 1) ИЛИ (бит 3 равен 1) = (хотя бы один из битов 0,3,4 не равен 1) — т.е. инверсия не(А) = А = (Х&25 не равно 0).

В итоге мы заметили, что если А=8, то наше выражение принимает вид F = не(А) ИЛИ А, что, по закону исключённого третьего, всегда тождественно истинно. При других, меньших, значениях А независимость от значения Х получить не удаётся, т.к. маски выходят разные. Ну, а при наличии в старших битах А единиц в битах выше 4 ничего не меняется, т.к. в остальных масках у нас нули. Получается, что только при А=8 формула превращается в тавтологию для произвольного Х.

 

Дмитрий Лисин

newtonew.com

ЕГЭ по информатике задание 18 — Информатика в школе

ЕГЭ по информатике задание 18

Тема: «Логические выражения и множества».

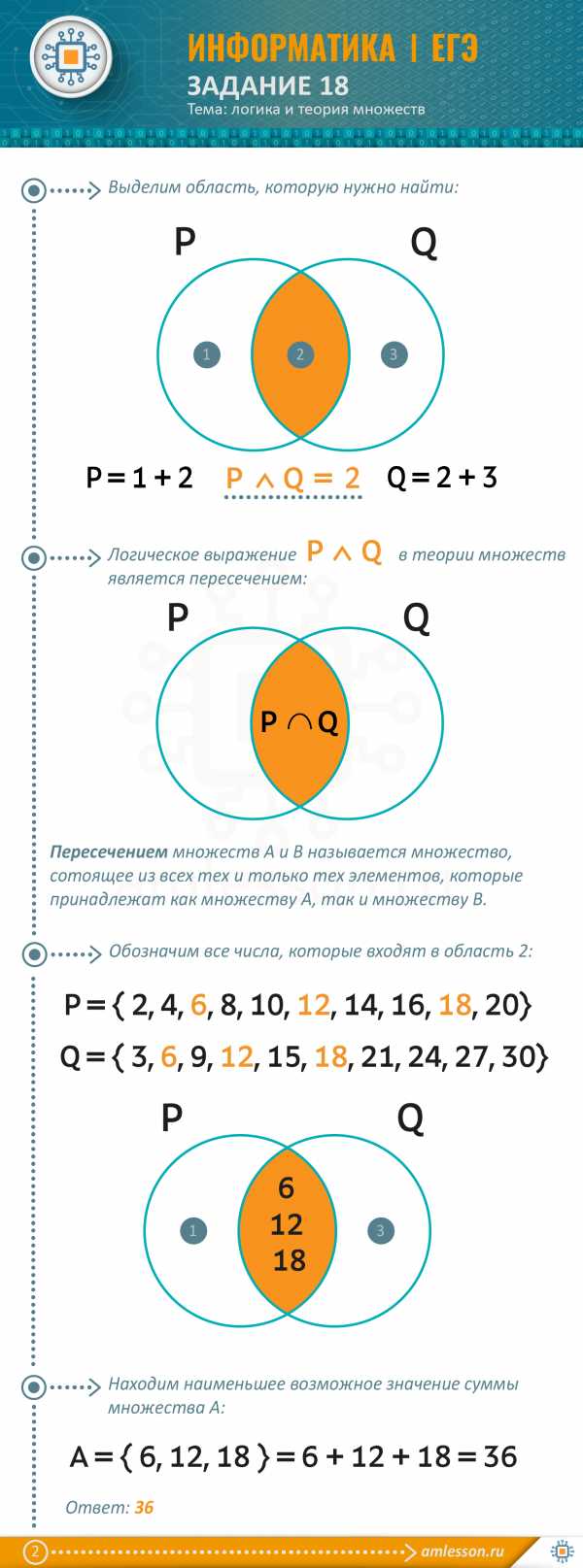
Элементами множеств A, P, Q являются натуральные числа, причём P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение

 

истинно (т.е. принимает значение 1) при любом значении переменной x. Определите наименьшее возможное значение суммы элементов множества A.

Данный пример взят из учебно-методического издания «Информатика и ИКТ. Подготовка к ЕГЭ 2018 году. Диагностические работы. — М: МЦНМО, 2018.»

Данную книгу вы можете купить здесь

РЕШЕНИЕ

Еще один вид задания  ЕГЭ по информатике задание 18. Отрезки

Задание №18 ЕГЭ по информатике проверяет знания по темам:

 

amlesson.ru

Информатика — Задание 18. Разбор отдельных задач.

1. Задачи в формате ЕГЭ 2012 г.

2. Задачи в формате ЕГЭ-2013-2014 гг.

      Статья К.Ю.Полякова (после перехода по ссылке прокрутите 3 страницы вниз )

     Другие материалы К.Ю.Полякова вот здесь

3. Задачи в формате ЕГЭ-2015-2016 гг.

 

1. Задачи в формате ЕГЭ 2012 г.

1. Пример из демонстрационного варианта

     Какое из приведённых имён удовлетворяет логическому условию:

(первая буква согласная → вторая буква согласная) / (предпоследняя буква гласная → последняя буква гласная)

1) КРИСТИНА         2) МАКСИМ             3) СТЕПАН               4) МАРИЯ

     Набросок решения  Импликация a  → b равносильна выражению ¬a / b.

Первая импликация верна для слов КРИСТИНА и СТЕПАН. Из этих слов вторая импликация верна только для слова КРИСТИНА.

Ответ: 1. КРИСТИНА

 2.Еще два примера

  Пример 1 (открытый сегмент банка ФИПИ)

Какое из приведённых имён удовлетворяет логическому условию:

(первая буква согласная → первая буква гласная) / (последняя буква гласная → последняя буква согласная)

1. ИРИНА       2. МАКСИМ    3. АРТЁМ    4. МАРИЯ

         Набросок решения . Импликация a  → b равносильна выражению ¬a / b. Это выражение истинно если или выражение a ложно, или оба выражения a и b истинны. Поскольку в нашем случае ни в одной из импликаций оба выражения одновременно истинными быть не могут, то должны быть ложными утверждения «первая буква согласная» и «последняя буква гласная», то есть нам нужно слово, у которого первая буква гласная, а последняя — согласная.

Ответ: 3. АРТЁМ.

  Пример 2. Для какого из указанных значений числа X истинно высказывание

(X < 4)→(X >15 )

            1)  1     2) 2      3) 3      4) 4

Решение. Никакое число не может быть одновременно меньше 4 и больше 15. Поэтому импликация истинна только, если посылка X < 4 ложна.

Ответ 4.

 

2. Задачи в формате ЕГЭ 2013-2014 гг.

2.1. Демо-версия 2013 г. 

На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14].

Выберите такой отрезок A, что формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

 

1) [0, 3]                2) [3, 11]              3) [11, 15]            4) [15, 17]

 2.2. Демо-версия 2014 г. 

На числовой прямой даны два отрезка: P = [1, 39] и Q = [23, 58].  Выберите из предложенных отрезков такой отрезок A, что логическое выражение

 ( (x ∈ P) → ¬ (x ∈  Q) )→ ¬ (x ∈  А)

тождественно истинно, то есть принимает значение 1 при любом значении переменной

Варианты ответов:   1)[5, 20]    2)[25, 35]     3)[40, 55]      4)[20, 40]

Решение.  Преобразуем выражение, используя эквивалентные преобразования логических выражений. Имеем:

¬( (x ∈ P) → ¬ (x ∈  Q) )   ∨ (¬ (x ∈  А) )  — замена импликации дизъюнкцией;

¬( ¬(x ∈ P)     ∨  ¬ (x ∈  Q) )   ∨ (¬ (x ∈  А) )  — замена импликации дизъюнкцией;

( (x ∈ P)    ∧  (x ∈  Q) )   ∨ (¬ (x ∈  А) )  — правило де Моргана и снятие двойного отрицания;

(x ∈  А) → ( (x ∈ P)    ∧  (x ∈  Q) )  — замена дизъюнкции импликацией

(x ∈  А) →  (x ∈ P∩ Q)   — переход к пересечению множеств

Последнее выражение является тождественно истинным тогда и только тогда, когда A ⊆ P∩ Q = [1, 39] ∩ [23, 58] = [23, 39]  (см. здесь). Из четырех данных отрезков этому условию удовлетворяет только отрезок [25, 35]  — вариант №2.

Ответ: [25, 35]  — вариант №2

 

3. Задачи в формате ЕГЭ 2015-2016 гг.

3.1. Задача 1.

 На числовой прямой даны два отрезка: P = [5, 10] и Q = [20, 30].

Известно, что границы отрезка A  — целочисленные точки и для отрезка A, формула

( (x ∈ А) → (x ∈  P) ) \/ (x ∈  Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Какова наибольшая возможная длина отрезка A?

Правильный ответ:    10

Решение:

Преобразуем выражение – заменим импликацию дизъюнкцией. Получим:

(¬(x ∈  А))  \/ ( (x ∈  P) ) \/ (x ∈  Q)

Выражение ((x ∈  P) ) \/ (x ∈  Q) истинно для тех только тех x, которые лежат либо в P, либо в Q, иными словами – для x ∈  R = P ∪ Q =[5, 10] ∪ [20, 30].  Выражение

(¬(x ∈  А))  \/ (x ∈  R)

тождественно истинно тогда и только тогда, когда  A ∈  R. Так как A – отрезок, то A ∈  R тогда и только тогда, когда A ∈  P или A ∈  Q. Так как отрезок Q длиннее отрезка P, то наибольшая длина отрезка A достигается, когда A = Q = [20, 30]. Длина отрезка A в этом случае равна 30 – 20 = 10.

3.2. Задача 2.

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110₂&0101₂ = 0100₂ = 4.  Для какого наименьшего неотрицательного целого числа А формула

x&25 ≠ 0 → (x&33 ≠ 0 → x&А ≠ 0)

 тождественно истинна, т.е. принимает значение 1 при любом неотрицательном целом значении переменной х?

Правильный ответ:    57

Решение:

Преобразуем выражение – заменим импликации дизъюнкциями. Получим:

¬(x&25 ≠ 0)  ∨ (¬(x&33 ≠ 0)  ∨  x&А ≠ 0)

Раскроем скобки и заменим отрицания неравенств равенствами:

 x&25 = 0  ∨  x&33 = 0  ∨  x&А ≠ 0               (*)

Имеем: 25 = 11001₂ и 33 = 100001₂.  Поэтому формула

x&25 = 0  ∨  x&33 = 0

ложна тогда и только тогда, когда двоичная запись числа x  содержит 1 хотя бы в одном из следующих двоичных разрядов: 100000 (32), 10000 (16), 1000 (8) и 1.

Чтобы формула (*) была истинна при всех таких x необходимо и достаточно, чтобы двоичная запись числа A содержала 1 во всех этих разрядах. Наименьшее такое число – это число 32+16+8+1 = 57.

 

 

ege-go.ru

Разбор 18 задания ЕГЭ 2018 по информатике и ИКТ из демонстрационного варианта

Разбор 18 задания ЕГЭ 2018 по информатике и ИКТ из демоверсии. Это задание повышенного уровня сложности. Примерное время выполнения задания 3 минуты.

Проверяемые элементы содержания:
— Знание основных понятий и законов математической логики.

Элементы содержания, проверяемые на ЕГЭ:
— высказывания,
— логические операции,
— кванторы,
— истинность высказывания.

Задание 18

Для какого наибольшего целого числа А формула

((x ≤ 9) → (x⋅x ≤ A)) ⋀ ((y⋅y ≤ A) → (y ≤ 9))

тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?

Ответ: ________

Разбор 18 задания ЕГЭ 2018 по информатике

Разделим наше выражение на 2 части:

((x ≤ 9) → (x⋅x ≤ A)) = B
((y⋅y ≤ A) → (y ≤ 9)) = C

получаем

B ⋀ C

Главное действие в исходном выражении — это коньюнкция. Конъюнкция истинна, когда все операнды истинны. Т.е. в задаче обе части B и C должны быть истинными.

Рассмотрим часть B:

если в выражении (x ≤ 9), х > 9, то часть В будет истинна независимо от А. Значит значение числа А влияет на решение только при выполнении условия:

x ≤ 9

теперь для того чтобы в части В, выражение было истинным, надо чтобы (x⋅x ≤ A) было истинным:

x⋅x ≤ A

(импликация 1 → 1 = 1)

таким образом получаем:

x ≤ 9
x² ≤ A

при любых x

Но нам нам необходимо найти наибольшее возможное А, поэтому надо ограничить его значения сверху, а данная часть выражения ограничивает только снизу:

возьмем наименьшее натуральное: x = 1, тогда A ≥ 1

Рассмотрим часть С:

если выражение (y ≤ 9) действительно истинно (т.е. y ≤ 9), то часть С будет истинна независимо от А. Значит значение числа А влияет на решение только при выполнении условия:

y > 9

теперь для того чтобы в части C, выражение было истинным, надо чтобы (y⋅y ≤ A) было ложным:

y⋅y > A

(импликация 0 → 0 = 1)

таким образом получаем:

y > 9
y² > A

при любых y

данная часть выражения ограничивает значения А сверху:

возьмем наименьшее возможное по условию натуральное: y = 10, тогда A А меньшее 100 — это А = 99

Ответ: 99

infedu.ru

Разбор 18 задания и демоверсия егэ по информатике 2019 ФИПИ

Задание 18. Элементы математической логики и теория множеств: демонстрационный вариант егэ информатика 2019; государственный выпускной экзамен 2019; тренировочные варианты ЕГЭ по информатике, тематические тестовые задания и задачи из тренажера по информатике 2019

*** КАНАЛ ЮТЬЮБ ***
 
ЕГЭ по информатике -> ЕГЭ 2019 -> ЕГЭ 2019
 

Разбор 18 задания. Демоверсия егэ по информатике 2019:

Для какого наибольшего целого неотрицательного числа А выражение
  
(48 ≠ y + 2x) ∨ (A
 
тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?

📹 Видеоразбор демоверсии егэ 2019

  ✍ Показать решение:

• Разделим общее выражение на две части. Выделим неизвестную часть красным:

(48 ≠ y + 2x) ∨ (A 

Неизвестная часть должна быть истинной, она обязательно будет истинна, если известная часть — ложь:

(48 ≠ y + 2x) ∨ (A  = 1
      01

Т.е. 48 ≠ y + 2x = 0 или y + 2x = 48. На графике это уравнение представляет линию. Из условия имеем два ограничения:(x > 0) and (y > 0). Отобразим линию для 1-й четверти, соответствующей положительным x и y:

y + 2x = 48  :
при x = 0, y = 48
при y = 0, 2x = 48 => x = 24

Возьмем некоторое значение A, например, A = 25, отметим его на графике белой областью так, чтобы выполнялось (A . По условию имеем, что все точки данной части отрезка прямой y + 2x = 48 должны принадлежать отмеченной белой области. Заштрихуем область для всех точек прямой (голубым цветом):

То есть все точки голубого квадрата должны находиться под отрезком линии (включая вершину (A, A)), и данный квадрат, соответствует максимальному значению A.

Наибольшее значение голубая область приобретает в точке пересечения прямой y + 2x = 48 с прямой y = x:

Далее решаем полученное линейное уравнение (для x = y):

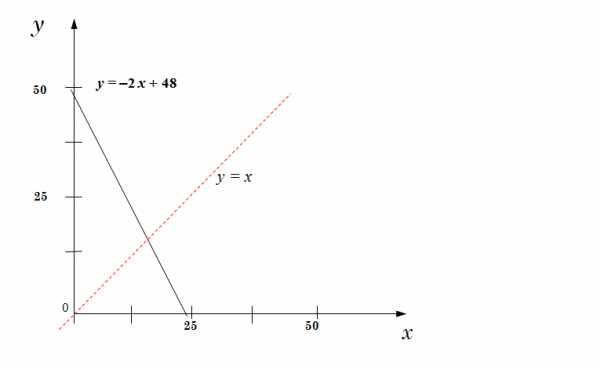
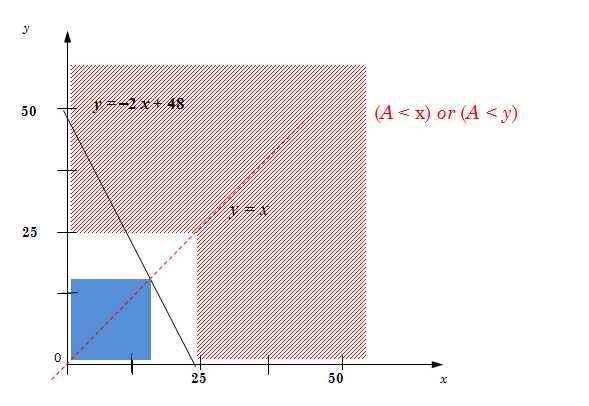
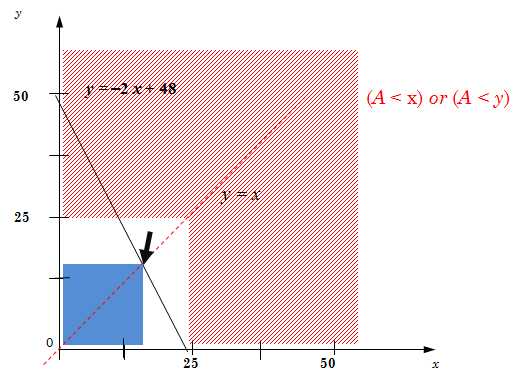
x + 2x = 48 =>
3x = 48
x = 16

Так как значение A должно быть меньше x, то наибольшее А = 15.

Результат: 15

labs.org.ru