Уравнения с параметром егэ: ЕГЭ. Задача 18. Задачи с параметром

{2}-3a-18\geq0; \end{array} \right . \end{array} \right .

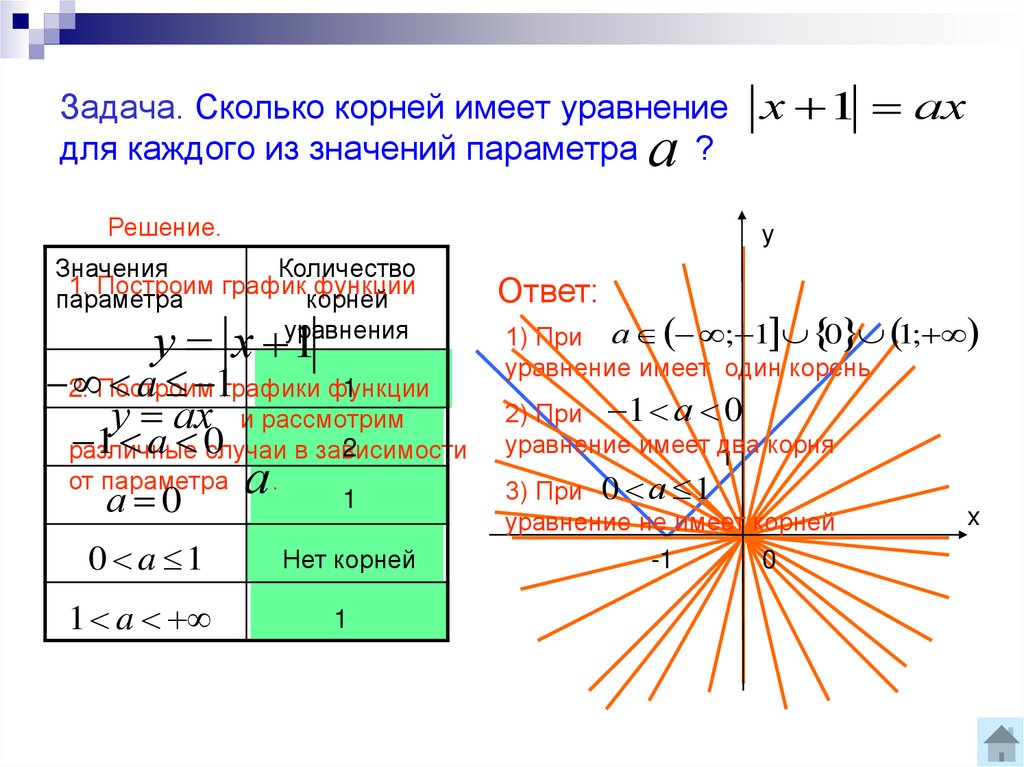
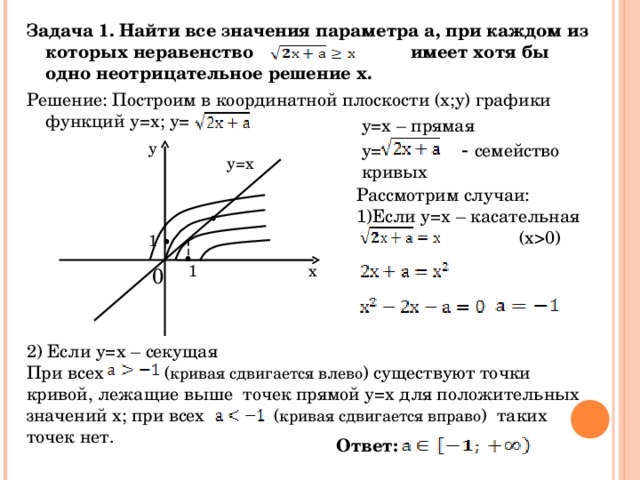
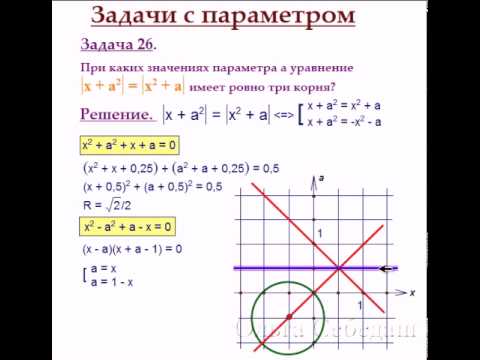
\left \{\!\!\!\! \begin{array}{l}\: a\geq 1,5, \\ \left [\!\! \begin{array}{l} (a-3)(a+2)\leq 0, \\ (a-6)(a+3)\geq0; \end{array} \right . \end{array} \right .

\left \{\!\!\!\! \begin{array}{l}\: a\geq 1,5, \\ \left [\!\! \begin{array}{l} a\leq -3, \\ -2\leq a\leq 3, \\ a\geq 6; \end{array} \right . \end{array} \right .

Ответ

1,5\leq a\leq 3; a\geq 6.

Источник: «Математика ЕГЭ 2016. Типовые тестовые задания». Под ред. И. В. Ященко.

Лучшие репетиторы для сдачи ЕГЭ

Математика

Русский язык

История

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Как подготовиться к решению задач с параметром на ЕГЭ

Личный кабинет

8 800 551-50-78 (бесплатно)

Онлайн подготовка к ЕГЭ-2023 по профильной математике

Подготовьтесь к ЕГЭ на 80+ баллов. Смотрите видео, читайте теорию, занимайтесь на онлайн-тренажерах

1С:Репетитор

8 800 551-50-78

Личный кабинет

1С:Репетитор – подготовка к ЕГЭ по математике

© ООО «1С-Софт» | ЧОУ ДПО «1С-ОБРАЗОВАНИЕ» | 2016–2022

8 800 551-50-78

Связаться с нами:

Главная

Задача с параметром – для обычного школьника одна из самых сложных задач варианта КИМ ЕГЭ: в программах по математике для общеобразовательных школ (за исключением профильных и специализированных классов, школ и лицеев) таким задачам либо не уделяется должного внимания, либо они не рассматриваются вовсе. Несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволяют продвинуться в решении задачи с параметром достаточно далеко и если уж не решить ее полностью, то хотя бы получить за нее некоторое количество баллов на экзамене.

Ранее, до появления единого государственного экзамена, задачи с параметрами входили в варианты вступительных экзаменов по математике в ведущие вузы, а сегодня входят в вариант КИМ ЕГЭ профильного уровня. Дело в том, что эти задачи обладают высокой диагностической ценностью: они позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности, а главное – насколько успешно он сможет овладеть курсом математики в вузе.

«Научите меня решать задачи с параметром», – такую просьбу я часто слышу от своих учеников. Что ж, эта задача потребует от выпускника немало интеллектуальных усилий. С чего начать изучение? С освоения методов решения задач с параметром. Собственно, если вы внимательно читали наши рекомендации, как подготовиться к решению сложных задач варианта КИМ ЕГЭ, то заметили, что это универсальный совет. Именно так построен наш курс «1С:Репетитор»: изучаем как можно более широкий спектр методов и приемов решения задач и тренируемся в применении этих методов на практике.

Чему нужно научиться, решая задачи с параметром

В первую очередь – правильно применять равносильные преобразования уравнений, неравенств и их систем. То есть понять, при каких ограничениях, накладываемых на параметр, можно выполнять то или иное преобразование. Лучше всего начать с заданий вида: «Для каждого значения параметра решить…» и рассмотреть по возможности все основные элементарные функции, встречающиеся в школьном курсе математики.

Если с несложными задачами такого вида школьник справляется неплохо, то можно переходить к изучению аналитических методов решения задач, содержательно усложняя и классифицируя задачи с точки зрения применения к ним этих методов исследования. Имеется в виду знакомство с подходами к решению задач, содержащих формулировки типа: «При каких значениях параметра уравнение (неравенство, система) имеет одно (два, три, бесконечно много и т.д.) решений», «При каких значениях параметра решением уравнения (неравенства, системы) является некоторое подмножество множества действительных чисел» и т.д.

Следующий шаг, который мы рекомендуем, – тщательно изучить схему исследования квадратичной функции. Поскольку квадратичная функция является одной из самых хорошо изученных в школьном курсе математики, на ее основе можно предложить большое количество исследовательских задач, разнообразных по форме и содержанию, чем и пользуются составители вариантов КИМ ЕГЭ.

Мы рекомендуем подойти к рассмотрению данных задач по следующей схеме:

задачи, основанные на свойствах дискриминанта и старшего коэффициента квадратного трехчлена;

применение теоремы Виета в задачах с параметром;

расположение корней квадратного трехчлена относительно заданных точек;

более сложные задачи, сводящиеся к исследованию квадратного трехчлена.

Следующая тема курса – графические методы решения задач с параметром

Существует два принципиально различных подхода – построение графиков функций или уравнений в плоскости

(x; y) или в плоскости (x; a). Кроме того, для графического метода решения задач с параметром в плоскости (x; y) необходимо рассмотреть различные виды преобразования графиков – обычно это параллельный перенос, поворот прямой и гомотетия. Есть класс задач, решение которых основано на аналитических свойствах функций (области определения, области значений, четности, периодичности и т. д.), эти свойства и приемы их использования тоже нужно знать.

На этом перечень методов решения задач с параметрами, разумеется, не заканчивается, но анализ вариантов КИМ ЕГЭ профильного уровня и практика показывают, что в настоящее время этого достаточно для успешного решения задачи № 18 на экзамене.

В заключение отметим, что выстроить подобный курс самостоятельно, без преподавателя, обычный школьник не сможет, даже имея под рукой хорошие учебные пособия по методам решения задач с параметром. Здесь необходима помощь опытного наставника, который сможет подобрать нужные задачи и выстроить траекторию движения школьника по ним.

Заметим, кстати, что весьма эффективным инструментом для изучения именно методов решения задач с параметром являются интерактивные тренажеры с пошаговым разбором решения.

Работая с таким тренажером, школьник одновременно учится выстраивать логику решения задачи с параметром и контролирует правильность выполнения каждого шага решения. Это очень важное умение, так как одна из основных сложностей в решении задачи с параметром состоит в том, что необходимо на каждом шаге решения понимать, что означают уже полученные результаты и что (в зависимости от этих результатов) еще остается сделать, чтобы довести решение до конца.

Регулярно тренируйтесь в решении задач

Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:

• Начать заниматься бесплатно.
• Купить доступ к этой задаче в составе экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.

Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.

Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.

Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Разбор задач с параметрами из ЕГЭ по математике, по теме задачи с параметром ЕГЭ, как решать задание 18 в экзамене ЕГЭ, задачи с параметром ЕГЭ, задания с параметром ЕГЭ, задача 18 ЕГЭ, модуль и окружности, решение параметров ЕГЭ, решение задачи 18, система уравнений с параметром, научиться решать задачи с параметрами, сложных задач варианта КИМ ЕГЭ, начертить графики функций, ЕГЭ по математике профильного уровня, методы решения уравнений и неравенств, выпускникам 11 класса в 2018 году, поступающим в технический вуз.

Уравнения — ADS 2009 — Keysight Knowledge Center

Перейти к концу метаданных

Уравнения выполняют сложные математические операции с данными. Вы можете отображать результаты уравнений на графиках отображения данных, что позволяет вам анализировать информацию различными способами.

В этом разделе описывается, как писать уравнения и как отображать результаты. Он включает примеры использования некоторых математических выражений в Advanced Design System. Справочник по доступным функциям можно найти в Интернете, к нему можно получить доступ с

диалоговое окно уравнений .

Уравнения могут быть простыми или очень сложными. Уравнение может включать:

• Математические выражения и операции
• Функции
• Другие уравнения отображения данных
• Переменные набора данных
• Информация о наборе данных
• Маркировочные этикетки

Правила написания выражений минимальны:

• Уравнения чувствительны к регистру
• Имена уравнений не могут начинаться с цифры
• Все функции должны выполняться с использованием заданного синтаксиса
• Скобки используются для определения порядка операций
• Зарезервированные имена нельзя использовать в качестве переменных уравнения. Например, вы не можете использовать mag в качестве переменной mag=[1::3] .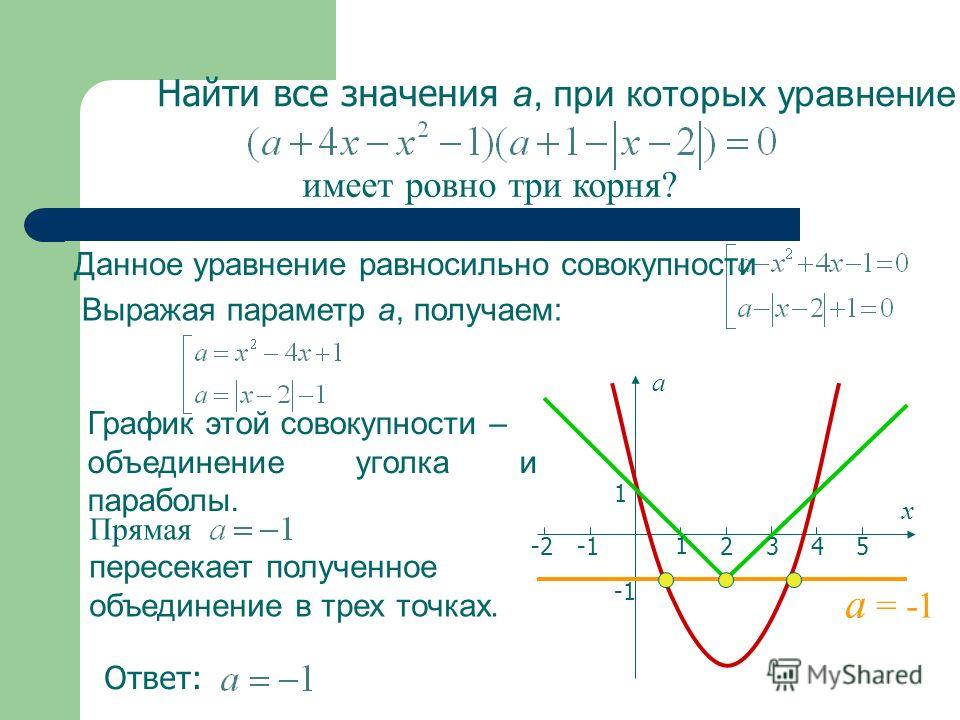
  Вместо этого его нужно использовать как mymag=[1::3] или что-то подобное.

Вставка уравнений

Чтобы вставить уравнение в дисплей данных:

1. Нажмите кнопку Equation на палитре или выберите Вставить > Уравнение .
2. Наведите указатель на область отображения и щелкните мышью. Появится диалоговое окно «Введите уравнение».

3. Введите уравнение с именем переменной уравнения слева и выражением справа. Пример уравнения показан ниже.
   
   Выражение может включать любой из элементов предыдущего списка. Обратите внимание, что имя набора данных не требуется, если переменная набора данных включена в набор данных по умолчанию.
   Нажмите кнопку Справка по функциям , чтобы просмотреть алфавитный список ссылок на доступные функции измерения. Щелкните вкладку Index в левом фрейме документации Measurement Expressions для дополнительного метода прокрутки списка функций.
4. Чтобы добавить в уравнение переменную набора данных, поместите курсор в то уравнение, куда вы хотите вставить переменную.
5. Выберите имя набора данных из списка.
6. Представлен список переменных в наборе данных. Выберите переменную из этого списка и нажмите Вставить .
7. Чтобы изменить свойства отображения выражения, щелкните Свойства уравнения . Дополнительные сведения см. в разделе Редактирование текста.
8. Установите флажок Показать иерархию , чтобы отобразить переменные набора данных в формате дерева. Дополнительные сведения см. в разделе Использование обозревателя набора данных.
9. Нажмите кнопку Управление наборами данных , чтобы найти набор данных, недоступный в текущем проекте. Дополнительные сведения см. в разделе Псевдоним набора данных.
10. Нажмите кнопку Информация о переменной , чтобы открыть диалоговое окно Обзор данных. Если щелкнуть переменную набора данных в списке диалогового окна «Обзор данных», в правой части диалогового окна отобразится подробная информация о переменной набора данных. Дополнительные сведения см. в разделе Просмотр информации о переменных.
11. Когда уравнение завершено, нажмите ОК .

Сокращение имен переменных

При использовании переменных в наборе данных по умолчанию имена переменных набора данных могут быть сокращены, чтобы упростить чтение уравнения, при условии, что каждое имя остается уникальным. Например, если переменная введена как:
Curve_Tracer.Sweep1.DC1.DC.IC.i

Если эта переменная находится в наборе данных по умолчанию, вы можете стереть все с последнего периода и сохранить IC.i

Если вы хотите использовать переменную с тем же именем, но из другого набора данных в проекте, вы не можете удалить часть имени любой переменной. Имена переменных должны быть уникальными.

Если вы вводите данные из наборов данных, которые находятся за пределами проекта, вводится полный путь к файлу. Вы можете сохранить полный путь или удалить ту часть пути к файлу, которая является общей для текущего проекта.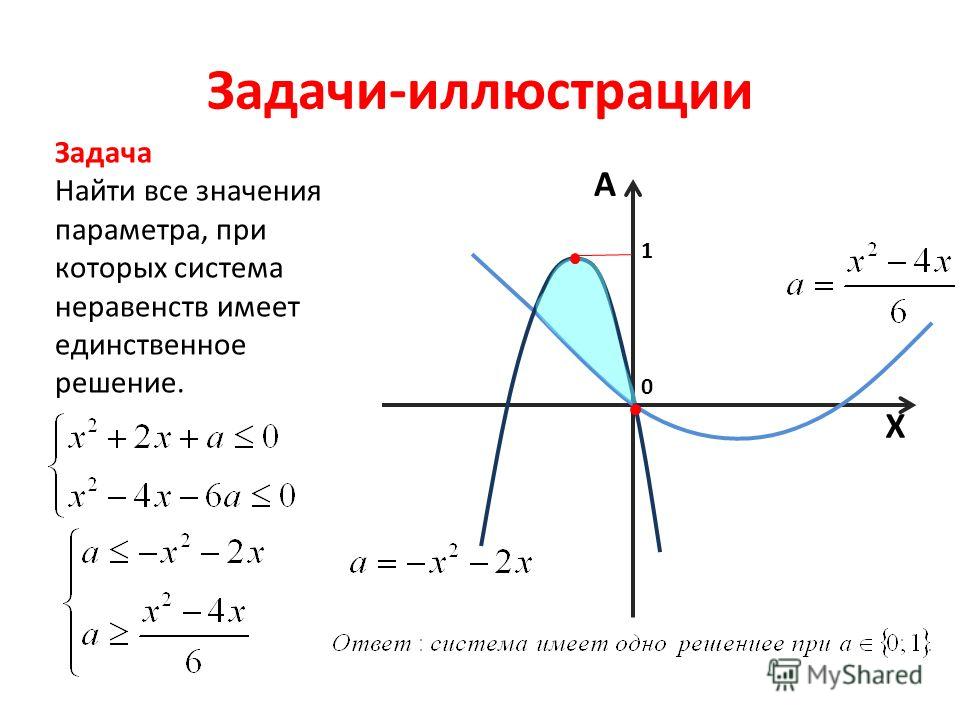

Просмотр данных из нескольких наборов данных

Список наборов данных по умолчанию позволяет ссылаться только на один набор данных. Если у вас есть несколько уравнений, вы можете легко изменить ссылочные наборы данных, определив строковые переменные с именем набора данных и ссылаясь на строковую переменную в уравнениях. Например:

MeasuredData=»measured»
MeasS21=db($MeasuredData..S(2, 1))
DiffS21=MeasS21 − SimS21
SimulatedData=»simulated»
SimS21=db($SimulatedData..S(2, 1))

Вставка условных выражений

Редактор уравнений DDS также позволяет вводить условные выражения. Вы можете использовать оператор if then else , как показано в следующем примере:

x = если (частота > 100 МГц), то 0,001 иначе 1e99
 

Просмотр результатов уравнения

Результаты уравнения можно вывести на график или отобразить в виде списка. Вы обрабатываете результаты так же, как и любые другие данные. Вы можете применять маркеры, редактировать формат или использовать результаты уравнения в другом уравнении.

Чтобы просмотреть результаты вашего уравнения:

1. Нажмите кнопку Уравнение на палитре или выберите Вставка > Уравнение .
2. Поместите указатель на область отображения и щелкните мышью, чтобы открыть диалоговое окно «Ввод уравнения».
3. Выберите Уравнения из списка Наборы данных и уравнения.
4. Выберите переменную уравнения и нажмите кнопку Вставить .
   Если уравнение введено неверно, отображается сообщение об ошибке. Некоторые типы ошибок в формуле вызывают выделение идентификатора формулы ( Eqn ) на дисплее данных красным цветом. Другие ошибки вызовут появление диалогового окна ошибки. В этом диалоговом окне содержится конкретная информация об ошибке.
5. Будет использоваться тип трассировки по умолчанию для выбранных данных. Если вы хотите проверить или изменить тип трассировки, щелкните Параметры трассировки и перейдите к редактированию трассировки.
6. Щелкните OK , чтобы закрыть диалоговое окно и отобразить результаты уравнения.
   

Результаты уравнения также могут отображаться в текстовых объектах. Дополнительные сведения см. в разделе «Внедрение уравнений в текстовые объекты».

Работа с многомерными данными

Нередко при моделировании сканируется более одного параметра. Данные таких симуляций сохраняются как многомерные данные. Если вы хотите выполнить вычисления или отобразить только часть данных из таких симуляций, вам нужно использовать уравнения для выбора подмножеств данных.

Пример трассировщика кривых используется для иллюстрации того, как это сделать. Пример находится в каталоге Examples в подкаталоге MW_Ckts. В этом подкаталоге откройте проект LNA_prj, а затем откройте схему Curve_Tracer, которая является частью этого проекта.

Чтобы открыть отображение данных, в окне схемы трассировщика выберите Window > Open Data Display и выберите Curve_Tracer.dds .

См. схему. В этом примере базовый ток IBB и напряжение коллектор-эмиттер, VCE , изменяются следующим образом: IBB устанавливается на 5 мА, а VCE изменяется от 0 В до 3 В с шагом 0,1 В. При каждом приращении 0,1 В вычисляется IC и сохраняется в наборе данных. Когда этот цикл завершен, IBB увеличивается до 5 мА, VCE изменяется от 0 В до 3 В, и при каждом приращении 0,1 В IC измеряется и сохраняется в наборе данных. Это повторяется до IBB соответствует 30 мА; выполняется окончательная развертка VCE , и моделирование завершается.

См. дисплей данных. Трассировщик кривой представляет собой всю совокупность точек данных IC . Эти данные хранятся в наборе данных, и далее описывается структура хранения данных.

Некоторые измерения, такие как EVM в окне схемы DSP, обрабатывают каждую точку развертки как отдельную симуляцию и возвращают одну точку данных. Каждая точка данных содержит свипируемую переменную, результаты моделирования и нулевой индекс.
Чтобы отобразить такие данные, создайте выражение, такое как my_evm = E [ : : , 0], чтобы извлечь нулевой индекс выражения развертки.

Структура данных

На основе разверток моделирования имеется шесть значений для IBB и 31 значение для VCE . Индекс IBB 0-5, индекс VCE 0-30. Для каждой из этих комбинаций VCE и IBB была рассчитана и сохранена в наборе данных IC .

Можно выбрать одну точку данных или последовательность данных. В следующем разделе описывается, как получить доступ к частям данных с помощью индексов.

Доступ к данным

Доступ к данным осуществляется по значениям индекса. Приведенное ниже уравнение возвращает значение IC , когда VCE = 0 В и IBB = 20 мА.

Введите уравнение и используйте список для отображения результатов. Информацию о том, как вводить уравнения, см. в разделе Вставка уравнений. Информацию о том, как отображать результаты уравнения, см. в разделе Просмотр результатов уравнения.

Для этого уравнения порядок индексов не имеет значения, но в целом имеет значение. В следующем разделе описывается порядок индексов.

Порядок индекса

Данные извлекаются по значениям индекса. Порядок индекса имеет решающее значение для возврата предполагаемых данных и зависит от того, как настроена симуляция. В моделировании трассировщика элемент Parameter Sweep ссылается на элемент имитации постоянного тока, а параметр имитации постоянного тока ( VCE ) свипируется на основе параметра развертки параметра ( IBB ). Порядок индексов от самого внешнего к самому внутреннему, поэтому индекс IBB предшествует индексу VCE .

Попробуйте получить другие точки данных, например:

x1=IC. i[1,0]
x2=IC.i[0,1]
x3=IC.i[1,30]

Просмотрите результаты в списках и сравните их с иллюстрацией структуры данных .

Доступ к последовательностям данных

Вы можете получить доступ к подмножествам данных, используя индексы. Вы можете либо указать диапазон, либо использовать подстановочные знаки.
Например, чтобы отобразить кривую только для IBB = 20 мА, введите в виде уравнения:

IBB20=IC.i[3,::]

Добавьте IBB20 к графику трассировщика для просмотра результатов.

Символы :: в уравнении являются подстановочными знаками. В этом уравнении подстановочный знак заменяет значение индекса VCE , поэтому используются все значения VCE и возвращается вся трассировка данных.

Чтобы отобразить только часть трассы, используйте последовательность:

Отображаются данные элементов с 10-го по 20-й. Приращение по умолчанию равно 1, поэтому эту последовательность также можно записать как 10::20 . Если вы хотите пропустить точки данных в последовательности, установите приращение на значение больше единицы.

Чтобы отобразить часть нескольких кривых, используйте две последовательности:

IBB20=IC.i[3::5,10::20]

Обратите внимание на результаты на графике трассировщика кривой.

Доступ к набору данных

Вы можете вернуть набор данных, используя подстановочный знак в первой позиции уравнения:

VCE5=IC.i[::,5]

В этом примере возвращаются значения IC , где VCE = 0,5 В.

Не отображать этот результат на существующем графике трассировщика кривых. Вместо этого вставьте новый график и добавьте данные в новый график. Оси на этом графике отличаются от осей кривой. VCE отложен по оси y как функция IBB , который отложен по оси x.

Можно изменить тип кривой с линейной на точечную и просмотреть отдельные точки данных.

Вы также можете написать то же уравнение, что и:

VCE5=IC.i[5]

Подстановочный знак в первой позиции предполагается.

Построение многомерных данных

При построении многомерных данных ось X зависит от того, отображаются ли данные с использованием одного значения индекса или с использованием подстановочного знака (::) для выбора всех значений индекса.

Функция what() возвращает измерения в записи набора данных и количество точек в каждом измерении. Ниже показано, что измерения в BudGain1 — это Component, X и freq.

Ниже показаны многомерные данные, построенные с использованием одного значения индекса (0) для частоты:

Поскольку частота является значением одного индекса, значение по оси X сдвигается влево к следующему измерению, которое в данном примере равно X.
Ниже показаны те же многомерные данные, построенные с использованием подстановочного знака для выбора всех значений индекса для частоты:

Поскольку частота представляет собой все значения индекса, значение по оси X является частотой. В этом примере частота была единственным значением, поэтому вы могли ожидать таких же результатов, как показано, используя одно значение индекса. Однако процедура построения графика не делает различий между случаем, когда подстановочный знак представляет одно значение индекса или несколько значений индекса.

Работа с S-параметрами свипирования

Если вы хотите получить доступ к подмножествам S-параметров свипирования, вам нужно использовать как обозначение индекса, так и обозначение S-параметров. В этом разделе описаны различные комбинации и возвращаемые результаты.

Настройка примера

Если вы хотите иметь пример для работы, настройте и выполните моделирование, описанное здесь. В противном случае перейдите к следующему разделу.

В этом примере добавляется развертка параметров к файлу Amplifier.dsn 9Схема 0008 в проекте SweptSparams_prj .

1. В главном окне щелкните каталог примеров.
2. Выберите Учебник .
3. Выберите SweptSparams_prj .
4. Выберите Файл > Копировать проект и сделайте копию проекта.
5. Откройте копию SweptSparams_prj .
6. Открыть схему Amplifier.dsn .
7. Добавьте параметр свипирования, изменив источник напряжения с помощью элемента данных Var Eqn Data и элемента свипирования параметра, как показано ниже.
   
8. Повторно запустить симуляцию. Моделирование будет выполняться следующим образом: Vbias устанавливается на 3 В, и моделирование S-параметров выполняется на каждой частоте, указанной в элементе моделирования S-параметров, а S-матрицы сохраняются в наборе данных; Vbias устанавливается на 3,9 В, выполняется еще один набор симуляций S-параметров, которые сохраняются в наборе данных; это продолжается до тех пор, пока Vbias не станет равным 2,0 В, после чего выполняется окончательный набор симуляций S-параметров и вся симуляция завершается.
9. По завершении моделирования откройте новое окно отображения данных.
10. Установить набор данных по умолчанию на усилитель .
11. Вставьте прямоугольный график и добавьте к нему S(2,1). Отображается вся коллекция точек данных S(2,1), которые были рассчитаны для каждой точки частоты и для каждого значения Vbias .

В следующем разделе описывается, как данные хранятся в наборе данных.

Структура данных

На основе разверток моделирования существует одиннадцать значений для Vbias и значения 200 для freq . Индекс для Vbias равен 0-10, индекс для freq равен 0-199. Для каждой из этих комбинаций Vbias и freq, S-матрица была рассчитана и сохранена в наборе данных.

Порядок индексов такой же, как описано в Порядок индексов. То есть самый внешний индекс — первый, самый внутренний — последний. В приведенном выше примере первая позиция — это индекс Vbias , вторая — freq 9. 0008 .

Доступ к данным

Вы можете получить доступ к S-параметрам, используя индексы. Уравнение ниже возвращает S ₂₁ , рассчитанное для Vbias = 2,9 В и freq = 5 МГц:

myS21=S21[1,0]

Введите уравнение и используйте список для отображения результатов. Информацию о том, как вводить уравнения, см. в разделе Вставка уравнений. Информацию о том, как отображать результаты уравнения, см. в разделе Просмотр результатов уравнения.

Приведенное ниже уравнение возвращает S ₂₁ на всех частотах для одного значения Vbias ( Vbias =2V):

S21at2V=S21[10,::]

Добавьте этот результат на график. Подстановочный знак :: используется для замены индекса freq , поэтому возвращаются все значения freq , что позволяет отображать полную трассировку результатов S ₂₁ .

Чтобы отобразить только часть кривой, используйте последовательность:

Отображаются данные элементов с 50-го по 199-й. Шаг по умолчанию равен 1, и последовательность может быть записана как 50::199 . Если вы хотите пропустить точки данных в последовательности, установите приращение на значение больше единицы.

Чтобы отобразить часть нескольких трасс, используйте две последовательности:

S21block=S21[2::10,90::140]

Добавьте это на график и запишите результаты.

Доступ к развертке данных

Вы можете вернуть развертку данных, используя подстановочный знак в первой позиции уравнения:

column=S21[::,80]

В этом примере возвращается S ₂₁ для каждого значения Vbias на частоте с индексом 80.
Не наносите этот результат на существующий график трассировщика кривых. Вместо этого вставьте новый график и добавьте данные в новый график. Оси на этом графике отличаются от осей кривой. S ₂₁ откладывается по оси y как функция Vbias , которая откладывается по оси x.

Можно изменить тип кривой с линейной на точечную и просмотреть отдельные точки данных.

Вы также можете написать то же уравнение, что и:

столбец=S[80]

Подстановочный знак в первой позиции предполагается.

Работа с S-матрицей

S-параметры хранятся в S-матрице. В общем, вы, вероятно, захотите работать с конкретным S-параметром, а не со всей матрицей. Однако вы можете получить доступ ко всей матрице. Если не указать S-параметр, уравнение с использованием S возвращает всю S-матрицу:
myMatrix=S[1,0]

Таким же образом можно использовать индексы без указания S-параметра и возвращать S-матрицу в каждой точке:
manyMatrices=S[2::5, 80::90]

Используйте список для отображения результатов . Используйте кнопки прокрутки, чтобы просмотреть весь список данных. Как видите, возвращается большое количество данных.

Используйте функцию what для просмотра информации о переменной, включая:

• Независимые переменные
• Количество точек данных
• Размер матрицы
• Тип данных, например действительный или комплексный

Если переменная содержит одно число или одномерную последовательность чисел (например, строку или столбец), она называется Scalar . Если данные являются двумерными, они называются матрицей , и указывается размер матрицы. Примеры двух переменных из примера S-параметра с разверткой, Vbias и S-матрицы, S , показаны ниже. Дополнительные сведения об этих переменных см. в разделе «Настройка примера».

Поиск индекса

Объем данных в этом моделировании является двумерным и относительно небольшим, и несложно определить значения параметров развертки, которые соответствуют индексам. Для более сложных задач вы можете использовать функцию find_index() . Функция find_index() возвращает индекс, соответствующий значению данных. Например, в примере Curve_Tracer VCE — это скаляр, содержащий 61 точку данных. Уравнение ниже возвращает индекс, когда VCE равно 3 В:

Функция find_index() работает только со скалярными данными. VCE указывается с использованием индексов, чтобы представить его в скалярном формате.

Использование маркеров в уравнениях

Вы можете добавлять метки маркеров к уравнениям и выполнять операции с данными маркеров. Операция выполняется над данными зависимого маркера.

Чтобы добавить маркер к уравнению:

1. Нажмите кнопку Уравнение на палитре или выберите Вставка > Уравнение .
2. Наведите указатель на область отображения и щелкните мышью.
3. Появится диалоговое окно «Введите уравнение». Введите уравнение.
4. В точке, где вы хотите добавить маркер, выберите Уравнения __ из списка Наборы данных и уравнения __.
5. Выберите метку маркера и нажмите Вставить .
6. Завершите уравнение, затем нажмите OK .

Маркеры можно рассматривать как любые другие переменные в уравнении.

Использование независимых данных маркера

Вы можете получить независимые данные в маркере. Вы можете сделать это, используя функцию indep . Например:
myequation=indep(m1)
, где m1 — метка маркера. Вы также можете вложить это в другую функцию.

Маркеры на полярных графиках и диаграммах Смита возвращают данные в сложном формате. Возможно, вы захотите работать только с мнимой частью числа, которую вы можете получить с помощью image 9.Функция 0008. На следующем рисунке показана диаграмма Смита, маркер, примененный к трассе, уравнение, используемое для выделения мнимой составляющей, и список для проверки правильности уравнения.

Создание гистограммы после анализа методом Монте-Карло

Пример в этом разделе демонстрирует простую гистограмму с использованием данных из примера Tutorial/yldex1_prj. Пример симулирует частотную характеристику трансформатора импеданса со значениями компонентов, измененными во время анализа выхода. Дополнительные сведения о создании гистограммы см. в разделе Использование статистического моделирования.

Простая гистограмма с использованием данных из примера Tutorial/yldex1_prj

• Первый график простой гистограммы с использованием данных из примера Tutorial/yldex1_prj выше показывает все кривые дБ(S21).
• Второй график показывает распределение дБ(S21) на одной конкретной частоте, заданной уравнением «freq_index».
• Синтаксис S21[::,freq_index] выбирает значения S21 для всех итераций Монте-Карло на частоте «freq_index».
• Переменная NumBins просто устанавливает количество интервалов гистограммы.

Использование предопределенных уравнений

Отображение данных имеет набор предопределенных уравнений, которые можно использовать для отображения и документирования текущих свойств данных, таких как имя набора данных по умолчанию и путь.

В следующей таблице перечислены доступные предопределенные уравнения:

Имя предопределенного уравнения	Описание
Default_Dataset_Name	Имя текущего набора данных по умолчанию. Это имя не включает расширение «.ds»
Путь_набора_данных_по умолчанию	Полный путь к каталогу, содержащему набор данных по умолчанию
Default_Dataset_Modified_Time	Время последнего изменения файла набора данных по умолчанию
Default_Dataset_Modified_Date	Дата последнего изменения файла набора данных по умолчанию
Default_Dataset_Size	Размер в байтах набора данных по умолчанию
Имя_файла_DDS	Текущее имя файла DDS без расширения «. dds»
DDS_File_Path	Путь к каталогу, содержащему текущий файл DDS
DDS_File_Modified_Time	Время последнего изменения файла DDS
DDS_File_Modified_Date	Дата последней модификации файла DDS
DDS_File_Size	Размер файла DDS в байтах

Информацию о наборе данных можно отобразить двумя способами: с помощью текстового объекта или списка.
Чтобы отобразить информацию о наборе данных в текстовом объекте, см. раздел «Внедрение свойств набора данных в текстовые объекты».

Чтобы отобразить информацию о наборе данных в виде списка…

1. Выберите List из палитры или выберите Insert > Plot , затем щелкните мышью на странице, чтобы разместить график и отобразить диалоговое окно Plot Traces & Attributes.