ЕГЭ по математике, подготовка к ЕГЭ по математике 2021 в Москве, шкала перевода баллов — Учёба.ру
Что требуется
Решить планиметрическую задачу.
Особенности
Под этим номером может быть два варианта задания. Первый вариант: в задаче два пункта — а и b. В пункте a требуется что-то доказать, в пункте b — что-то найти. Могу сказать, что чаще всего надо начинать решать эту задачу именно с пункта b, а уже решение этого пункта поможет доказать пункт а. Как правило, абитуриентам проще что-то найти, чем доказать.
Второй вариант: задача без подпунктов. Здесь чаще всего скрыт подводный камень: задача требует рассмотрения двух случаев и приводит к двум разным ответам. Например, в условии задачи сказано, что окружности касаются в точке A, но не сказано каким образом, внешним или внутренним. Часто бывает так, что выпускник рисует один рисунок и возможно даже находит правильный ответ. А второй случай он не рассматривает, в результате чего получает ровно половину баллов за это задание.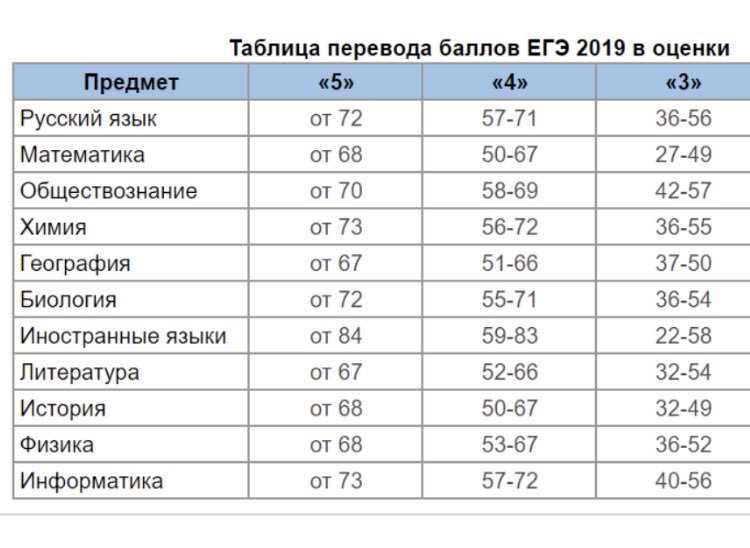
Советы
Необходимое условие для решения этой задачи — хорошее владение теоретическим материалом, например, из классического учебника по геометрии для 7-9 классов (Л.С. Атанасян). Необходимо знать формулировки аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства и формулы. Изучите дополнительные методы: метод дополнительного построения, метод подобия, метод замены, метод введения вспомогательного неизвестного, метод удвоения медианы, метод вспомогательной окружности, метод площадей.
Также здесь важен рисунок. 80% успеха геометрической задачи — это правильно нарисованный рисунок. Сделайте большой, хороший, наглядный рисунок, не экономьте на нем место.
И последнее, лайфхак для абитуриента — для решения задач по планиметрии выучите пять формул площади треугольника: через высоту и основание, через две стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности и формулу Герона.
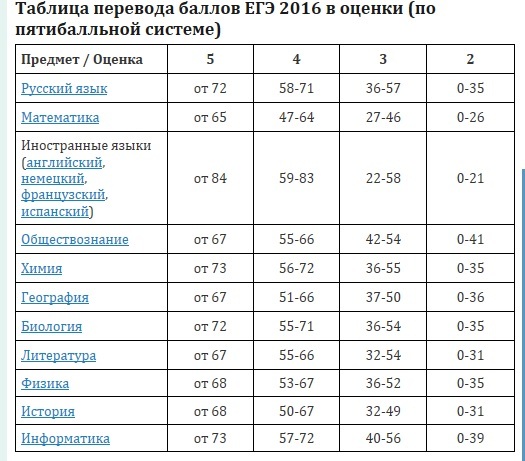
Шкала перевода баллов ЕГЭ 2021: минимальные баллы и таблица
Система оценивания и перевод баллов ЕГЭ вызывают много вопросов. Сколько баллов нужно получить по каждому предмету, чтобы выдали аттестат? Что такое первичный и вторичный балл? Влияет ли оценка за экзамен на итоговую отметку в аттестате? Давайте разбираться вместе.
Сколько баллов нужно получить по каждому предмету, чтобы выдали аттестат? Что такое первичный и вторичный балл? Влияет ли оценка за экзамен на итоговую отметку в аттестате? Давайте разбираться вместе.
Минимальные баллы ЕГЭ
Выпускники, которые собираются поступать за границу, обычно выбирают для сдачи только русский язык и математику. Самым важным для них становится средний балл аттестата. Им достаточно следующих баллов:
- Русский язык — 24
- Математика — 27
- Математика база — 3 (оценка)
А что, если не получилось уехать за границу? Можно ли поступить в российский вуз с минимальными баллами?
В 2021 году Минобрнауки установило следующий порог для поступления в вузы:
- Русский язык — 40
- Математика профильного уровня — 39
- Информатика и ИКТ — 44
- Биология — 39
- История — 35
- Химия — 39
- Иностранные языки — 30
- Физика — 39
- Обществознание — 45
- Литература — 40
- География — 40
По таким баллам в высшее учебное заведение можно поступить либо по целевому набору, либо по льготе. Балл по русскому языку должен быть выше. Кроме того, базовая математика, как результат, во вторичные баллы не переводится и при поступлении не учитывается.
Балл по русскому языку должен быть выше. Кроме того, базовая математика, как результат, во вторичные баллы не переводится и при поступлении не учитывается.
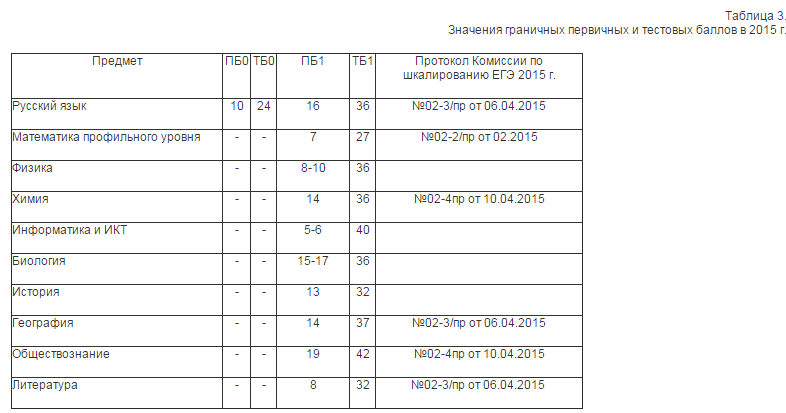
Шкала перевода баллов из первичных в стобалльные
Самое загадочное в формате ЕГЭ — перевод первичных баллов во вторичные.
Шкалирование — это процедура перевода первичных баллов в тестовые. Сперва выставляется первичный балл — это сумма баллов за все правильно выполненные задания. Первичный балл переводится в тестовый (вторичный), который учитывается при поступлении в вуз.
Обычно это делается автоматически. Вместе с результатами экзамена, где указаны первичные баллы с отчетом о каждом задании (правильно/не правильно), приходят вторичные, уже переведенные в стобалльную систему. Но всегда ведь хочется знать заранее, сколько заданий нужно сделать, чтобы получить, например, 85 баллов по информатике.
Проще всего, пожалуй, с английским языком. Максимально за экзамен можно набрать 100 первичных баллов, которые автоматически превращаются во вторичные. С остальными экзаменами сложнее, потому что для каждого предмета устанавливается свое соответствие.
С остальными экзаменами сложнее, потому что для каждого предмета устанавливается свое соответствие.
Кроме того, в каждом экзамене есть задания, за выполнение которых первичные баллы приносят больше вторичных.
Но узнать это заранее невозможно, так как каждый год производится индивидуальный расчет по каждому предмету на основе результатов работ всех выпускников, которые отсылаются в Москву и там анализируются.
Тем не менее, мы составили примерную таблицу перевода первичных баллов во вторичные на 2021.
Примечание: Чтобы попасть в топовые учебные заведения, такие как МГИМО или МГУ, даже ста баллов может не хватить. Поэтому будьте внимательны ко всему, что приносит дополнительные баллы — итоговому сочинению по литературе, олимпиадам, аттестату с отличием и т.д.
| Задания 1 — 12 | Каждое из заданий с 1 по 12 считается выполненным верно, если экзаменуемый предоставил ответ в виде целого числа либо конечной десятичной дроби.  Каждое правильно выполненное задание оценивается на 1 балл. Каждое правильно выполненное задание оценивается на 1 балл. |
| Задание 13 | Получены верные ответы в обоих пунктах с развернутым решением –
2 балла. Получен правильный ответ в пункте а или б, либо Решение задения не верно – 0 баллов. |
| Задание 14 | Обоснованно получены верные ответы в пунктах а и б – 2 балла. Выполнен только один из пунктов – а или б – 1 балл. Решение не соответствует ни одному из критериев, |
| Задание 15 | Получен правильный ответ с последовательным и аргументированным решением – 2 балла. Обоснованно получен ответ, отличающийся от правильного (не верно Решение задачи не верное – 0 баллов. |
| Задание 16 | Имеется правильное доказательство утверждения пункта «а», и аргументированно получен правильный ответ в пункте «б» – 3 балла. Получен правильный ответ в пункте «б», либо имеется верное доказательство утверждения пункта «а», и при аргументированном решении пункта «б» получен неправильный ответ из-за арифметической ошибки – 2 балла. Имеется верное доказательство утверждения пункта «а», Решение задачи не верное – 0 баллов. |
| Задание 17 | Аргументированно получен правильный ответ – 3 балла Правильно построена математическая модель, решение сведено к
исследованию этой модели, однако, решение задачи не завершено – 1 балл. Решение задачи не правильное, либо отсутствует – 0 баллов. |
| Задание 18 | Аргументированно получен правильный ответ – С помощью правильного рассуждения получено множество С помощью правильного рассуждения получена часть Правильно получена хотя бы одна граничная точка искомого Решение не соответствует ни одному из критериев, |
| Задание 19 | Правильно получены все перечисленные результаты
Верно получены три из указанных результатов – 3 балла Верно получены два из указанных результатов – 2 балла Верно получен один из указанных результатов – 1 балл. Решение задачи не верное, либо отсутствует. |
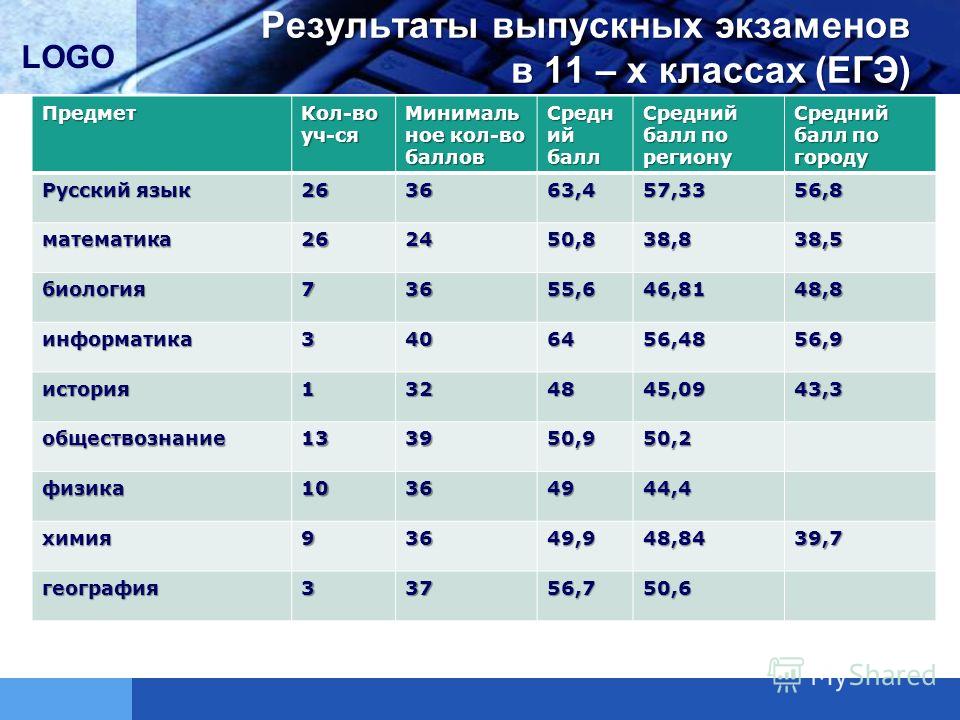
Все про баллы ЕГЭ 2021 по математике
— Сколько баллов можно получить за первую часть профильной математики?
— Сколько баллов дают за каждое задание ЕГЭ 2021 по математике (профильный уровень)?
— Перевод баллов ЕГЭ 2021 по профильной математике?
Вопросы с которыми давайте разберемся.
Сколько баллов дается за каждое задание по профильной математике на ЕГЭ 2021 можно узнать в демоверсии.
Распределение баллов ЕГЭ 2021 по заданиям — математика профиль
| № задания | Первичные баллы |
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
| 10 | 1 |
| 11 | 1 |
| 12 | 1 |
| 13 | 2 |
| 14 | 2 |
| 15 | 2 |
| 16 | 3 |
| 17 | 3 |
| 18 | 4 |
| 19 | 4 |
| Всего | 32 |
Математика профиль:
1 балл — за 1-12 задания.
2 балла — 13-15.
З балла — 16, 17.
4 балла — 18, 19.
Всего: 32 балла
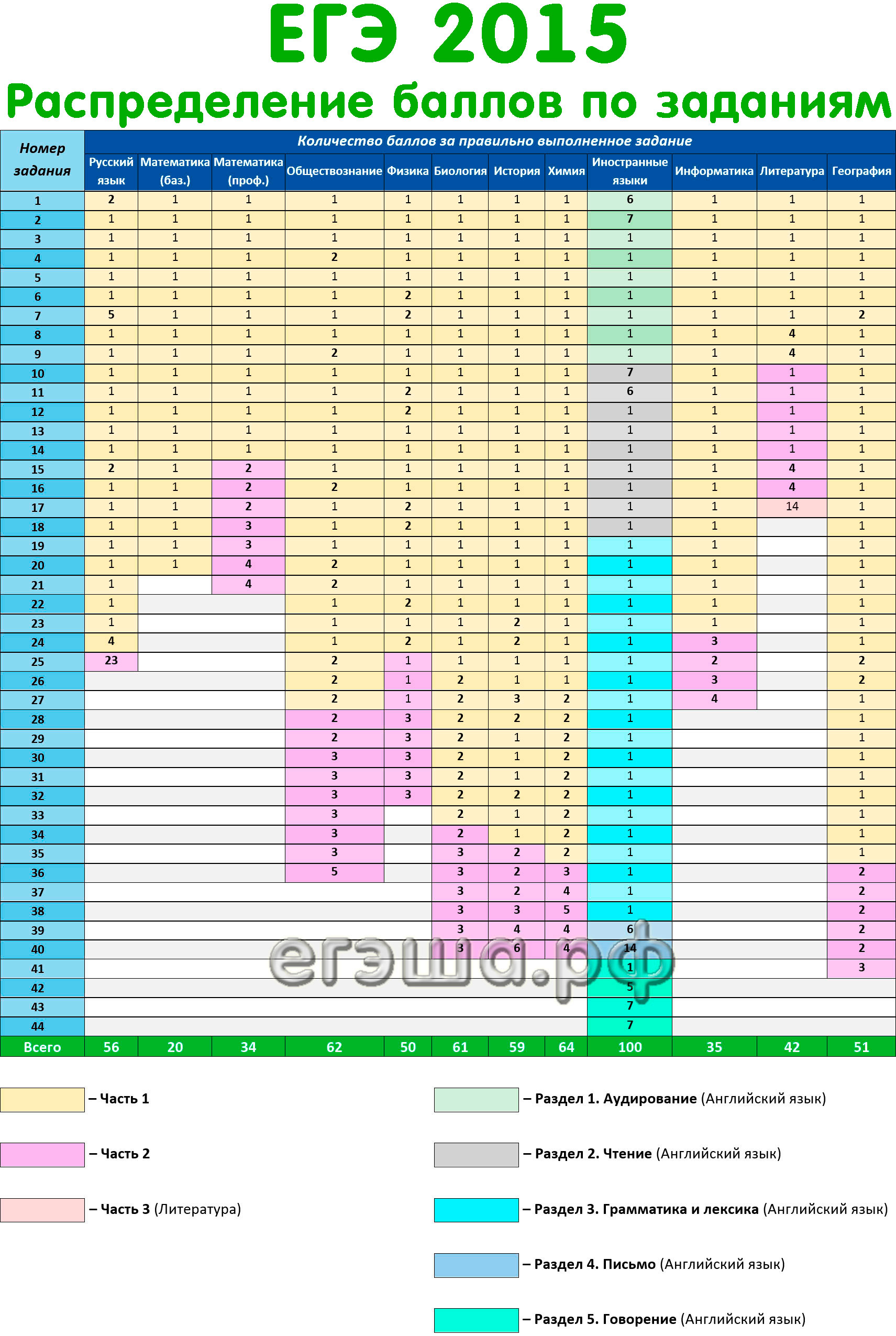
Соответствие первичных баллов тестовым
| Первичный балл |
Тестовый балл | Примечание |
| 1 | 5 | |
| 2 | 9 | |
| 3 | 14 | |
| 4 | 18 | |
| 5 | 23 | |
| 6 | 27 | Порог для получения аттестата |
| 7 | 33 | |
| 8 | 39 | |
| 9 | 45 | |
| 10 | 50 | |
| 11 | 56 | |
| 12 | 62 | |
| 13 | 68 | Минимальный балл для ВУЗА |
| 14 | 70 | |
| 15 | 72 | |
| 16 | 74 | |
| 17 | 76 | |
| 18 | 78 | |
| 19 | 80 | |
| 20 | 82 | |
| 21 | 84 | |
| 22 | 86 | |
| 23 | 88 | |
| 24 | 90 | |
| 25 | 92 | |
| 26 | 94 | |
| 27 | 96 | |
| 28 | 98 | |
| 29 | 99 | |
| 30 | 100 | |
| 31 | 100 | |
| 32 | 100 |
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 8 заданий (задания 1–8) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 4 задания (задания 9–12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).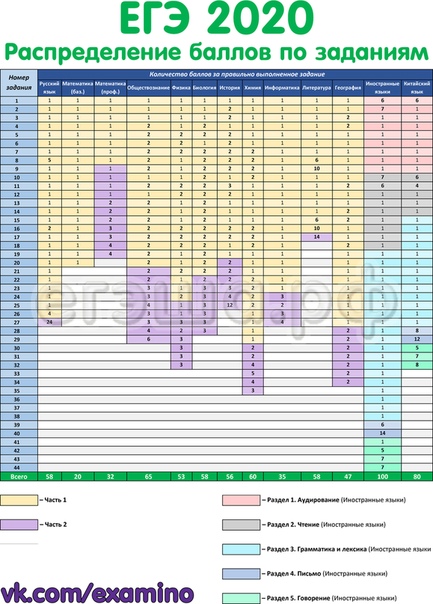
Таким образом, за решение первой части можно набрать 8 первичных баллов → 39 тестовых.
Связанные страницы:
Как оценивается ЕГЭ по математике – критерии и баллы
Подробно критерии оценивания ЕГЭ по математике профильного и базового уровней изложены в конце демоверсий и в спецификациях контрольных измерительных материалов. С обязательным экзаменом, который сдается для получения аттестата, все просто: каждое из верно выполненных 20 заданий принесет один балл, а в сумме и в переводе в привычную шкалу – пятерку. А вот ответы на вопросы ЕГЭ по математике профильного уровня оцениваются не столь однозначно: за решение сложных задач можно заработать от одного до четырех баллов. Итак, обо всем по порядку.Минимум по ЕГЭ по математике
Для получения аттестата хватит тройки. Профильный экзамен считается сданным, если набран эквивалент отметки удовлетворительно – 27 тестовых баллов. Многие вузы устанавливают эту же отметку в качестве минимально достаточной для подачи заявлений при поступлении на специальности, требующие углубленного знания математики. Но не факт, что с такой оценкой получится пройти на бюджет.
Многие вузы устанавливают эту же отметку в качестве минимально достаточной для подачи заявлений при поступлении на специальности, требующие углубленного знания математики. Но не факт, что с такой оценкой получится пройти на бюджет.
База
Минимальный первичный балл в текущем году равен 6. Именно столько надо набрать, чтобы получить аттестат. Решить можно любые из 20 заданий, в какой угодно комбинации.
Статистика оценок ЕГЭ по математике базового уровня в последние три года свидетельствует о том, что все большее число выпускников справляется с заданиями.
Преодолеть минимальный порог в прошлом году не смогли около 5 % школьников.
Профиль
Для профильного уровня ЕГЭ по математике установлен такой же минимальный порог, как и в базе (6 первичных, или 27 тестовых баллов). Их тоже можно получить за решение любых задач.
С минимумом, необходимым для сдачи профильного ЕГЭ по математике в прошлом году не справилось около 7,5 % участников экзамена.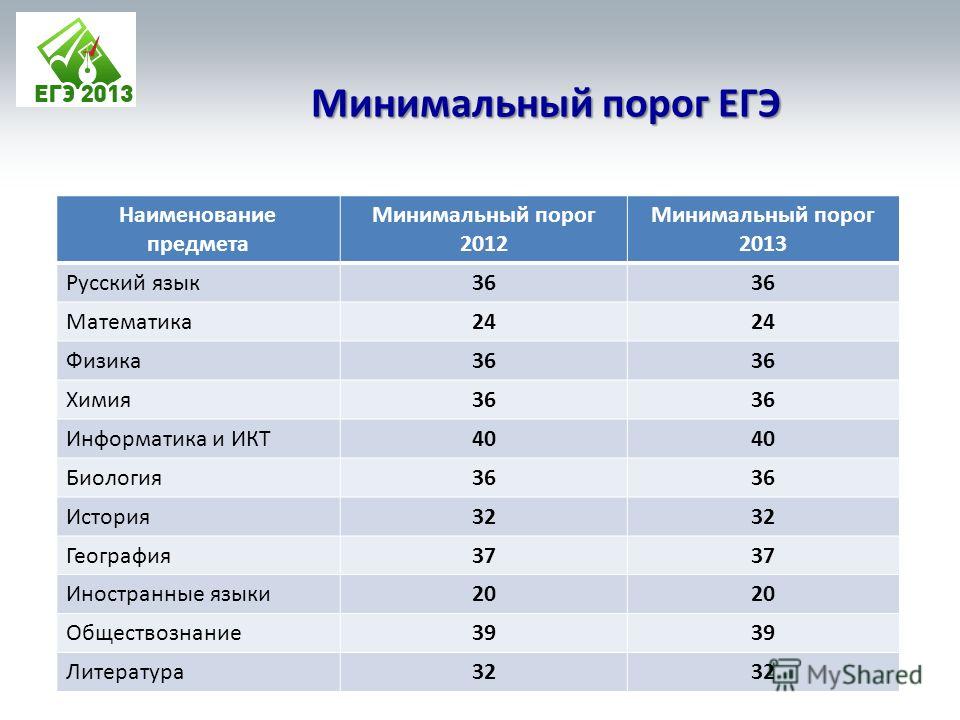
Доля выпускников, которым ЕГЭ по профильной математике оказался по силам, растет с каждым годом, и это обнадеживает.
Оценивание
На базовом ЕГЭ по математике за каждый правильный ответ засчитывается 1 балл. Критерий оценивания один – верное целое число или десятичная дробь, вписанные в соответствующее поле бланка для ответов. Если допущена ошибка, за задание выставляется ноль.
Баллы по математике ЕГЭ профильного уровня выставляются принципиально иным образом. За правильные ответы на простые задания начисляется 1 балл, за верно решенные сложные – от одного до четырех.
В общем виде система оценивания ЕГЭ по математике профильного уровня выглядит так:
- За решение первых 12 заданий засчитывается 1 балл. Несмотря на то что к базовому уровню сложности относятся всего 8 задач, часть усложненных вопросов также оценивается по минимуму. Это обусловлено тем, что ответы на них не предполагают наличия детального описания хода решения.
- За верное выполнение заданий под номерами 13,14,15 выставляется по два балла. Ответы проверяют эксперты (а не машина) на основе утвержденной системы оценивания работ.
- Правильное решение 16 и 17 заданий даст в общей сложности 6 баллов (по 3 за каждое).
- Максимально возможные баллы дают 2 последних задания (18 и 19) – за каждое из них можно получить по 4.
Причем критерии оценки усложненных задач предусматривают учет мнения проверяющего. Даже если школьник в итоге пришел к неверному ответу, но ход своих мыслей грамотно аргументировал, показал знание и владение предметом, то баллы за это задание ему все равно начисляются, но, сколько именно, будут решать эксперты.
Максимальные баллы за задания ЕГЭ по математике профильного уровня отражает таблица.
Таким образом, дав правильные ответы на все 19 вопросов, сопроводив часть из них (с 13 по 19) аргументацией, отражающей ход решения, участник экзамена может набрать максимальные 32 первичных балла, которые после перевода в тестовые станут заветными 100.
Разбалловка
Перевод в 100-балльную систему делается по разработанной ФИПИ шкале.
Многоэтажная формула, по которой рассчитывается перевод первичных баллов ЕГЭ по математике в тестовые, заставит крепко задуматься даже тех, кому по плечу без особого труда сдать профиль на 100 с плюсом. Поэтому просто примите к сведению, что 6 первичных соответствуют проходным 27 тестовым баллам.
Первичные баллы ЕГЭ по математике базового уровня по этой шкале не переводятся, они трансформируются в стандартные школьные оценки:
- от 0 до 6 баллов – неудовлетворительно, двойка;
- 7–11 – удовлетворительно, тройка;
- 12–16 – хорошо;
- 17–20 – отлично.
Перевод первичных баллов базового ЕГЭ по математике в стобалльную систему не предусмотрен, так как эти результаты не учитываются в конкурсе при поступлении в вузы.
Сколько заданий нужно решить на егэ по математике на 3
сколько заданий нужно решить на егэ по математике на 3
Репетитор по математике в Раменском
Шкала перевода баллов профильного ЕГЭ по математике
Ниже предлагается шкала перевода первичных баллов профильного ЕГЭ по математике в 2019 году:
- Набранный первичный балл переводится в тестовый.
Причём, можно заметить, что первая часть очень «дорогая» по баллам, за одно задание первой части можно получить 1 сырой балл, который перекодируется в 5 или 6 тестовых!
- Если решить верно все задачи первой части, то можно набрать 62 балла. Если решить всю первую часть, номер 13, 15 и 17 (чаще всего именно эти номера решают, те, кто имеет в школе твёрдую «5»), то можно набрать 80 баллов.
Скачай ЧЕК-ЛИСТ «ЕГЭ по математике» бесплатно! Алгоритм подготовки, литература, полезные ссылки, шкала баллов ЕГЭ.
- Далее баллы можно взять на геометрии (№14, 16), параметрах (№18) или теории чисел (№19). Если вы решили, например, №14, взяли пару баллов на №19, решив а) и б) – это уже 88 баллов.
 Таким образом, чтобы набрать Выше 80 баллов, нужно уметь решать задачи Хотя бы на одну из этих тем или на несколько:
Таким образом, чтобы набрать Выше 80 баллов, нужно уметь решать задачи Хотя бы на одну из этих тем или на несколько: Например, вы решили 12 задач, но в одной допустили ошибку, в результате получаете 11 первичных и 56 тестовых баллов, А могли бы получить 62 балла (!) , если бы не ошиблись в каком-то номере, это мог быть даже простейший №1. Ошибётесь ещё раз, получите уже 50 баллов за первую часть. Балл за простейшее задание №1 «весит» столько же, сколько один балл за сложную планиметрию №16, компьютеру всё равно, где вы его набрали. Главная стратегия — быть внимательным в первой части.
План экзаменационной работы ЕГЭ по математике
Работа рассчитана на 3 часа 55 минут. Если Вы планируете выполнять задания высокого уровня сложности под номерами 18-19, то на первую часть №1-12 у вас должно уходить не более 30 минут.
План экзаменационной работы ЕГЭ по математике
Ниже предлагается шкала перевода первичных баллов профильного ЕГЭ по математике в 2019 году:
- Набранный первичный балл переводится в тестовый.
 Каждое задание тестовой части «стоит» 1 балл. Задания письменной части — от 2 до 4 баллов Для прохождения порога по профильному ЕГЭ нужно решить не менее 6 задач, то есть набрать 6 первичных или 27 тестовых баллов.
Каждое задание тестовой части «стоит» 1 балл. Задания письменной части — от 2 до 4 баллов Для прохождения порога по профильному ЕГЭ нужно решить не менее 6 задач, то есть набрать 6 первичных или 27 тестовых баллов. Причём, можно заметить, что первая часть очень «дорогая» по баллам, за одно задание первой части можно получить 1 сырой балл, который перекодируется в 5 или 6 тестовых!
- Если решить верно все задачи первой части, то можно набрать 62 балла. Если решить всю первую часть, номер 13, 15 и 17 (чаще всего именно эти номера решают, те, кто имеет в школе твёрдую «5»), то можно набрать 80 баллов.
Скачай ЧЕК-ЛИСТ «ЕГЭ по математике» бесплатно! Алгоритм подготовки, литература, полезные ссылки, шкала баллов ЕГЭ.
- Далее баллы можно взять на геометрии (№14, 16), параметрах (№18) или теории чисел (№19). Если вы решили, например, №14, взяли пару баллов на №19, решив а) и б) – это уже 88 баллов.
 Таким образом, чтобы набрать Выше 80 баллов, нужно уметь решать задачи Хотя бы на одну из этих тем или на несколько:
Таким образом, чтобы набрать Выше 80 баллов, нужно уметь решать задачи Хотя бы на одну из этих тем или на несколько: Например, вы решили 12 задач, но в одной допустили ошибку, в результате получаете 11 первичных и 56 тестовых баллов, А могли бы получить 62 балла (!) , если бы не ошиблись в каком-то номере, это мог быть даже простейший №1. Ошибётесь ещё раз, получите уже 50 баллов за первую часть. Балл за простейшее задание №1 «весит» столько же, сколько один балл за сложную планиметрию №16, компьютеру всё равно, где вы его набрали. Главная стратегия — быть внимательным в первой части.
План экзаменационной работы ЕГЭ по математике
Работа рассчитана на 3 часа 55 минут. Если Вы планируете выполнять задания высокого уровня сложности под номерами 18-19, то на первую часть №1-12 у вас должно уходить не более 30 минут.
- Набранный первичный балл переводится в тестовый. Каждое задание тестовой части «стоит» 1 балл.
Репетитор по математике в Раменском
Главная стратегия быть внимательным в первой части.
Ramrepetitor. ru
29.07.2020 13:36:43
2020-07-29 13:36:43
ЕГЭ по математике, наравне с русским языком, – обязательный экзамен для сдачи выпускниками 11-х классов. По статистике он самый сложный.
Мы предлагаем ознакомиться с общей информацией об экзамене и сразу приступить к подготовке. Экзамен 2019 года не отличается от прошлого года – это касается и базового, и профильного варианта.
Базовый уровень ЕГЭ
Этот вариант подойдет для выпускников в двух случаях, если:
не понадобится математика для поступления в вуз; не собираетесь продолжать обучение после окончания школы.
Если в выбранной вами специальности присутствует графа с предметом «математика», то базовый уровень не ваш вариант.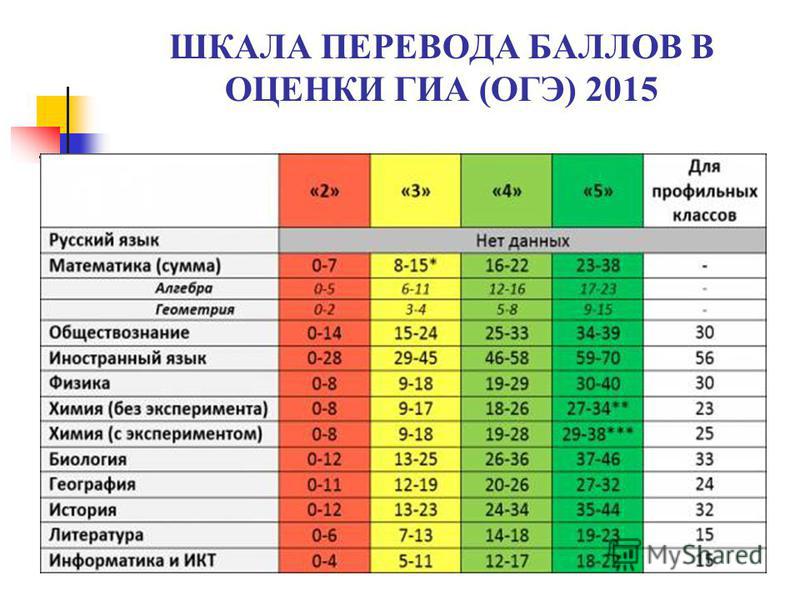
Оценивание базового экзамена
Формула перевода первичных баллов в тестовые каждый год обновляется и становится известной после проведения досрочного периода ЕГЭ. Уже вышло распоряжение Рособрнадзора, которое официально закрепило соответствие первичных и тестовых балов по всем предметам на 2019 год.
Согласно распоряжению, чтобы сдать базовый ЕГЭ по математике хотя бы на тройку, необходимо набрать 12 первичных баллов. Это равносильно правильному выполнению любых 12 заданий. Максимальный первичный балл – 20.
Структура базового экзамена
В 2019 году тест по математике базового уровня состоит из 20 заданий с кратким ответом, которым является целое число, или конечная десятичная дробь, или последовательность цифр. Ответ нужно либо посчитать, либо выбрать один из предлагаемых вариантов.
Профильный уровень ЕГЭ
Этот ЕГЭ в 2019 году не отличается от ЕГЭ прошлого года.
Именно профильный уровень выпускники должны сдавать для поступления в вузы, потому что в подавляющем большинстве специальностей математика указана как основной предмет для поступления.
Оценивание профильного теста
Здесь нет ничего специфичного: как обычно, вы набираете первичные баллы, которые потом переводятся в тестовые. И уже по 100-балльной системе можно определить отметку за экзамен.
Чтобы экзамен просто засчитали, достаточно набрать 6 первичных баллов. Для этого нужно решить хотя бы 6 заданий части 1. Максимальный первичный балл – 32.
Структура профильного теста
В 2019 году тест ЕГЭ по математике профильного уровня состоит из двух частей, включающих в себя 19 заданий.
- Часть 1: 8 заданий (1–8) базового уровня сложности с кратким ответом. Часть 2: 4 задания (9–12) повышенного уровня сложности с кратким ответом и 7 заданий (13–19) повышенного и высокого уровней сложности с развернутым ответом.
Подготовка к ЕГЭ
- ПройдитеТесты ЕГЭ онлайн бесплатно без регистрации и СМС. Представленные тесты по своей сложности и структуре идентичны реальным экзаменам, проводившимся в соответствующие годы.

- СкачайтеДемонстрационные варианты ЕГЭ по математике, которые позволят лучше подготовиться к экзамену и легче его сдать. Все предложенные тесты разработаны и одобрены для подготовки к ЕГЭ Федеральным институтом педагогических измерений (ФИПИ). В этом же ФИПИ разрабатываются все официальные варианты ЕГЭ. Ознакомьтесь с основными формулами для подготовки к экзамену, они помогут освежить память перед тем, как приступить к выполнению демонстрационных и тестовых вариантов.
Задания, которые вы увидите, скорее всего, не встретятся на экзамене, но будут задания, аналогичные демонстрационным, по той же тематике или просто с другими цифрами.
Мы предлагаем ознакомиться с общей информацией об экзамене и сразу приступить к подготовке. Экзамен 2019 года не отличается от прошлого года – это касается и базового, и профильного варианта.
Профильный уровень ЕГЭ
Этот ЕГЭ в 2019 году не отличается от ЕГЭ прошлого года.
Именно профильный уровень выпускники должны сдавать для поступления в вузы, потому что в подавляющем большинстве специальностей математика указана как основной предмет для поступления.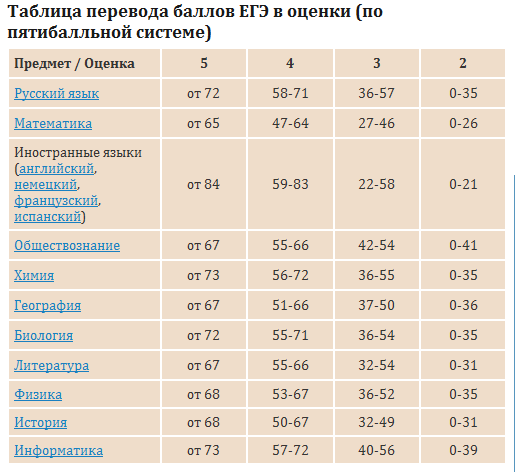
Оценивание профильного теста
Здесь нет ничего специфичного: как обычно, вы набираете первичные баллы, которые потом переводятся в тестовые. И уже по 100-балльной системе можно определить отметку за экзамен.
Чтобы экзамен просто засчитали, достаточно набрать 6 первичных баллов. Для этого нужно решить хотя бы 6 заданий части 1. Максимальный первичный балл – 32.
Структура профильного теста
В 2019 году тест ЕГЭ по математике профильного уровня состоит из двух частей, включающих в себя 19 заданий.
- Часть 1: 8 заданий (1–8) базового уровня сложности с кратким ответом. Часть 2: 4 задания (9–12) повышенного уровня сложности с кратким ответом и 7 заданий (13–19) повышенного и высокого уровней сложности с развернутым ответом.
Если в выбранной вами специальности присутствует графа с предметом «математика», то базовый уровень не ваш вариант.
Базовый уровень ЕГЭ
Мы предлагаем ознакомиться с общей информацией об экзамене и сразу приступить к подготовке.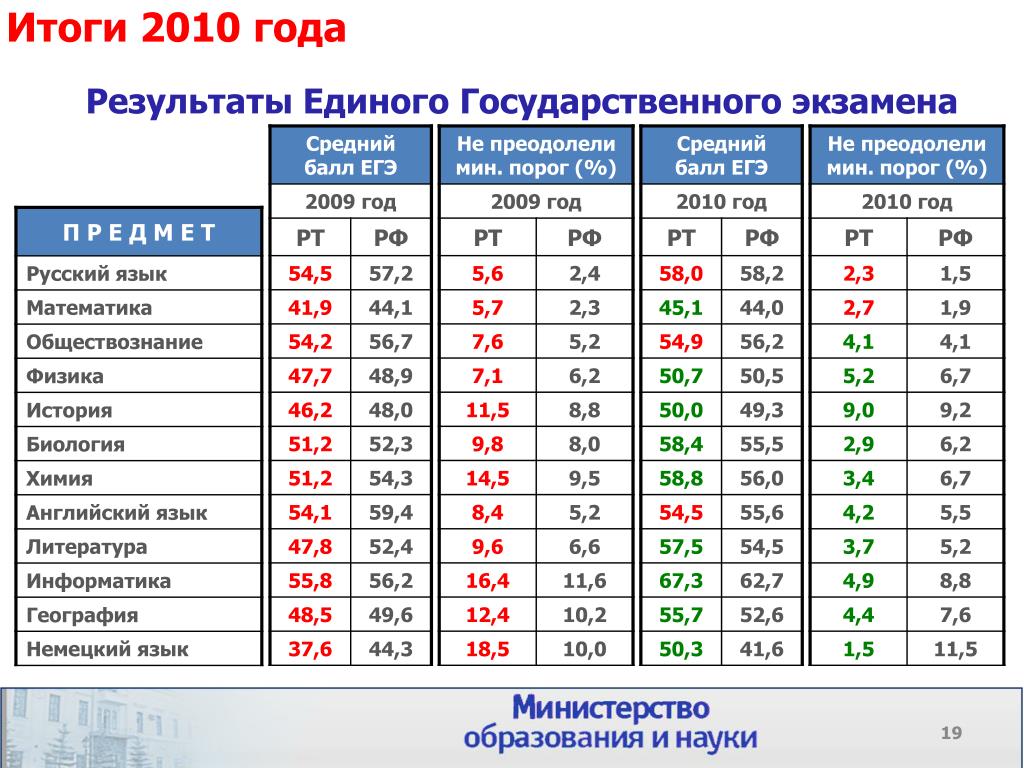
Www. examen. ru
25.10.2018 10:05:23
2018-10-25 10:05:23
Юлия Геннадьевна Оператор справочной
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, – 32 балла. Из них – за модуль «Алгебра» – 20 баллов, за модуль «Геометрия» – 12 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», – 8 баллов, набранные в сумме за выполнение обоих модулей, при условии, что из них не менее 2 баллов по модулю «Геометрия».
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:+
Для естественнонаучного профиля: 18 баллов, из них не менее 6 по геометрии;
Для экономического профиля: 18 баллов, из них не менее 5 по геометрии;
Физико-математического профиля: 19 баллов, из них не менее 7 по геометрии.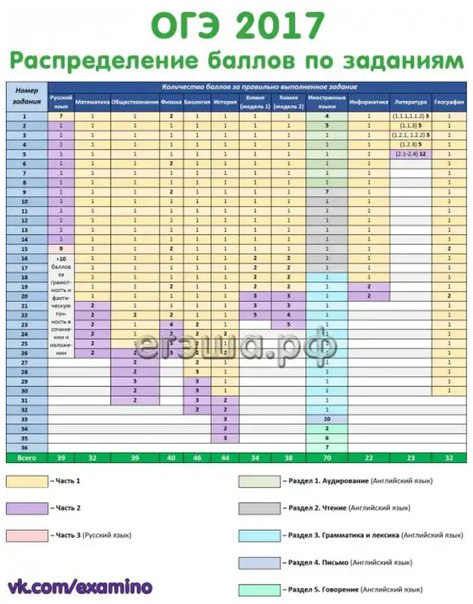
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, – 32 балла. Из них – за модуль «Алгебра» – 20 баллов, за модуль «Геометрия» – 12 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», – 8 баллов, набранные в сумме за выполнение обоих модулей, при условии, что из них не менее 2 баллов по модулю «Геометрия».
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:+
Юлия Геннадьевна Оператор справочной
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, – 32 балла. Из них – за модуль «Алгебра» – 20 баллов, за модуль «Геометрия» – 12 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», – 8 баллов, набранные в сумме за выполнение обоих модулей, при условии, что из них не менее 2 баллов по модулю «Геометрия».
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:+
Для естественнонаучного профиля: 18 баллов, из них не менее 6 по геометрии;
Для экономического профиля: 18 баллов, из них не менее 5 по геометрии;
Физико-математического профиля: 19 баллов, из них не менее 7 по геометрии.
Юлия Геннадьевна Оператор справочной
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы.
Www. spravkakirova. ru
25.03.2020 19:36:51
2020-03-25 19:36:51
Источники:
Http://ramrepetitor. ru/shkala-perevoda-ballov-profilnogo-ege-po-matematike/
Http://ramrepetitor. ru/shkala-perevoda-ballov-profilnogo-ege-po-matematike/
Https://www. examen. ru/add/ege/ege-po-matematike/
Https://www. spravkakirova. ru/skolko-nuzhno-reshit-zadanij-po-matematike-na-oge-chto-by-napisat-na-3-1280605
Сколько нужно решить заданий в егэ по математике на 3
сколько нужно решить заданий в егэ по математике на 3
Репетитор по математике в Раменском
Шкала перевода баллов профильного ЕГЭ по математике
Ниже предлагается шкала перевода первичных баллов профильного ЕГЭ по математике в 2019 году:
- Набранный первичный балл переводится в тестовый.
 Каждое задание тестовой части «стоит» 1 балл. Задания письменной части — от 2 до 4 баллов Для прохождения порога по профильному ЕГЭ нужно решить не менее 6 задач, то есть набрать 6 первичных или 27 тестовых баллов.
Каждое задание тестовой части «стоит» 1 балл. Задания письменной части — от 2 до 4 баллов Для прохождения порога по профильному ЕГЭ нужно решить не менее 6 задач, то есть набрать 6 первичных или 27 тестовых баллов. Причём, можно заметить, что первая часть очень «дорогая» по баллам, за одно задание первой части можно получить 1 сырой балл, который перекодируется в 5 или 6 тестовых!
- Если решить верно все задачи первой части, то можно набрать 62 балла. Если решить всю первую часть, номер 13, 15 и 17 (чаще всего именно эти номера решают, те, кто имеет в школе твёрдую «5»), то можно набрать 80 баллов.
Скачай ЧЕК-ЛИСТ «ЕГЭ по математике» бесплатно! Алгоритм подготовки, литература, полезные ссылки, шкала баллов ЕГЭ.
- Далее баллы можно взять на геометрии (№14, 16), параметрах (№18) или теории чисел (№19). Если вы решили, например, №14, взяли пару баллов на №19, решив а) и б) – это уже 88 баллов.
 Таким образом, чтобы набрать Выше 80 баллов, нужно уметь решать задачи Хотя бы на одну из этих тем или на несколько:
Таким образом, чтобы набрать Выше 80 баллов, нужно уметь решать задачи Хотя бы на одну из этих тем или на несколько: Например, вы решили 12 задач, но в одной допустили ошибку, в результате получаете 11 первичных и 56 тестовых баллов, А могли бы получить 62 балла (!) , если бы не ошиблись в каком-то номере, это мог быть даже простейший №1. Ошибётесь ещё раз, получите уже 50 баллов за первую часть. Балл за простейшее задание №1 «весит» столько же, сколько один балл за сложную планиметрию №16, компьютеру всё равно, где вы его набрали. Главная стратегия — быть внимательным в первой части.
План экзаменационной работы ЕГЭ по математике
Работа рассчитана на 3 часа 55 минут. Если Вы планируете выполнять задания высокого уровня сложности под номерами 18-19, то на первую часть №1-12 у вас должно уходить не более 30 минут.
Скачай ЧЕК-ЛИСТ «ЕГЭ по математике» бесплатно! Алгоритм подготовки, литература, полезные ссылки, шкала баллов ЕГЭ.
Ниже предлагается шкала перевода первичных баллов профильного ЕГЭ по математике в 2019 году:
- Набранный первичный балл переводится в тестовый. Каждое задание тестовой части «стоит» 1 балл. Задания письменной части — от 2 до 4 баллов Для прохождения порога по профильному ЕГЭ нужно решить не менее 6 задач, то есть набрать 6 первичных или 27 тестовых баллов.
Причём, можно заметить, что первая часть очень «дорогая» по баллам, за одно задание первой части можно получить 1 сырой балл, который перекодируется в 5 или 6 тестовых!
- Если решить верно все задачи первой части, то можно набрать 62 балла. Если решить всю первую часть, номер 13, 15 и 17 (чаще всего именно эти номера решают, те, кто имеет в школе твёрдую «5»), то можно набрать 80 баллов.
Скачай ЧЕК-ЛИСТ «ЕГЭ по математике» бесплатно! Алгоритм подготовки, литература, полезные ссылки, шкала баллов ЕГЭ.
- Далее баллы можно взять на геометрии (№14, 16), параметрах (№18) или теории чисел (№19).
 Если вы решили, например, №14, взяли пару баллов на №19, решив а) и б) – это уже 88 баллов. Таким образом, чтобы набрать Выше 80 баллов, нужно уметь решать задачи Хотя бы на одну из этих тем или на несколько:
Если вы решили, например, №14, взяли пару баллов на №19, решив а) и б) – это уже 88 баллов. Таким образом, чтобы набрать Выше 80 баллов, нужно уметь решать задачи Хотя бы на одну из этих тем или на несколько: Например, вы решили 12 задач, но в одной допустили ошибку, в результате получаете 11 первичных и 56 тестовых баллов, А могли бы получить 62 балла (!) , если бы не ошиблись в каком-то номере, это мог быть даже простейший №1. Ошибётесь ещё раз, получите уже 50 баллов за первую часть. Балл за простейшее задание №1 «весит» столько же, сколько один балл за сложную планиметрию №16, компьютеру всё равно, где вы его набрали. Главная стратегия — быть внимательным в первой части.
План экзаменационной работы ЕГЭ по математике
Работа рассчитана на 3 часа 55 минут. Если Вы планируете выполнять задания высокого уровня сложности под номерами 18-19, то на первую часть №1-12 у вас должно уходить не более 30 минут.
- Если решить верно все задачи первой части, то можно набрать 62 балла. Если решить всю первую часть, номер 13, 15 и 17 (чаще всего именно эти номера решают, те, кто имеет в школе твёрдую «5»), то можно набрать 80 баллов.
Репетитор по математике в Раменском
Алгоритм подготовки, литература, полезные ссылки, шкала баллов ЕГЭ.
Ramrepetitor. ru
11.02.2019 1:00:52
2019-02-11 01:00:52
Юлия Геннадьевна Оператор справочной
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, – 32 балла. Из них – за модуль «Алгебра» – 20 баллов, за модуль «Геометрия» – 12 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», – 8 баллов, набранные в сумме за выполнение обоих модулей, при условии, что из них не менее 2 баллов по модулю «Геометрия».
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:+
Для естественнонаучного профиля: 18 баллов, из них не менее 6 по геометрии;
Для экономического профиля: 18 баллов, из них не менее 5 по геометрии;
Физико-математического профиля: 19 баллов, из них не менее 7 по геометрии.
Юлия Геннадьевна Оператор справочной
Юлия Геннадьевна Оператор справочной
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, – 32 балла. Из них – за модуль «Алгебра» – 20 баллов, за модуль «Геометрия» – 12 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», – 8 баллов, набранные в сумме за выполнение обоих модулей, при условии, что из них не менее 2 баллов по модулю «Геометрия».
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:+
Для естественнонаучного профиля: 18 баллов, из них не менее 6 по геометрии;
Для экономического профиля: 18 баллов, из них не менее 5 по геометрии;
Физико-математического профиля: 19 баллов, из них не менее 7 по геометрии.
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, – 32 балла. Из них – за модуль «Алгебра» – 20 баллов, за модуль «Геометрия» – 12 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», – 8 баллов, набранные в сумме за выполнение обоих модулей, при условии, что из них не менее 2 баллов по модулю «Геометрия».
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:+
Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:+
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, 32 балла.
Www. spravkakirova. ru
20.06.2018 2:26:37
2018-06-20 02:26:37
Сколько заданий нужно сделать, чтобы сдать ЕГЭ по математике 2015?
Сколько необходимо сделать заданий, чтобы сдать ЕГЭ в 2015 году по математике.
Минимальное количество баллов на ЕГЭ по математике нынче отображает число 27. Для сравнения: 2014 год — 20 баллов.
И что же это значит? А вот что: Пять заданий части В и ни заданием меньше. Да ещё и правильно решить надо.
Так что начинайте готовиться уже сейчас, даже если математика не потребуется для дальнейшего поступления в вуз (а о каком поступлении вообще речь при минималке), то сдавать-то всё равно придётся, потому — обязательная дисциплина на ЕГЭ по окончании 11 класса!
Ищите и решайте пробные тесты, задавайте вопросы учителю по непонятным моментам. Готовьтесь!
Готовьтесь!
И учтите, что время экзамена раньше было четыре часа, а в этом году уменьшат на пять минут. Правда, не пойму — для чего и в связи с чем?
Минимальное количество баллов на ЕГЭ по математике нынче отображает число 27. Для сравнения: 2014 год — 20 баллов.
Сколько заданий нужно сделать, чтобы сдать ЕГЭ по математике 2015?
Сколько необходимо сделать заданий, чтобы сдать ЕГЭ в 2015 году по математике.
Минимальное количество баллов на ЕГЭ по математике нынче отображает число 27. Для сравнения: 2014 год — 20 баллов.
И что же это значит? А вот что: Пять заданий части В и ни заданием меньше. Да ещё и правильно решить надо.
Так что начинайте готовиться уже сейчас, даже если математика не потребуется для дальнейшего поступления в вуз (а о каком поступлении вообще речь при минималке), то сдавать-то всё равно придётся, потому — обязательная дисциплина на ЕГЭ по окончании 11 класса!
Ищите и решайте пробные тесты, задавайте вопросы учителю по непонятным моментам. Готовьтесь!
Готовьтесь!
И учтите, что время экзамена раньше было четыре часа, а в этом году уменьшат на пять минут. Правда, не пойму — для чего и в связи с чем?
Ищите и решайте пробные тесты, задавайте вопросы учителю по непонятным моментам. Готовьтесь!
Минимальное количество баллов на ЕГЭ по математике нынче отображает число 27.
Www. bolshoyvopros. ru
19.11.2019 11:58:05
2019-11-19 11:58:05
Источники:
Http://ramrepetitor. ru/shkala-perevoda-ballov-profilnogo-ege-po-matematike/
Https://www. spravkakirova. ru/skolko-nuzhno-reshit-zadanij-po-matematike-na-oge-chto-by-napisat-na-3-1280605
Http://www. bolshoyvopros. ru/questions/1152935-skolko-zadanij-nuzhno-sdelat-chtoby-sdat-ege-po-matematike-2015.html
4 СТРОКИ МАТЕМАТИЧЕСКИХ ЗНАНИЙ | Сложим: помощь детям в изучении математики
Fuson, K.C., & Burghardt, B.H. (1993). Групповые тематические исследования второклассников, изобретающих многозначные процедуры сложения десятичных блоков и письменных оценок. В J.R.Becker & B.J.Pence (Eds.), Proceedings of the пятнадцатого ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (стр. 240–246).Сан-Хосе, Калифорния: Государственный университет Сан-Хосе. (Услуга размножения документов ERIC № ED 372 917).
В J.R.Becker & B.J.Pence (Eds.), Proceedings of the пятнадцатого ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (стр. 240–246).Сан-Хосе, Калифорния: Государственный университет Сан-Хосе. (Услуга размножения документов ERIC № ED 372 917).
Fuson, K.C., Carroll, W.M., & Landis, J. (1996). Уровни осмысления и решения сложения и вычитания сравнивают словесные задачи. Познание и обучение , 14 , 345–371.
Гири, округ Колумбия (1995). Отражения эволюции и культуры в детском познании. Американский психолог , 50 (1), 24–37.
Грино Дж. Г., Пирсон П. Д. и Шонфельд А. Х. (1997). Последствия для NAEP исследований в области обучения и познания. В: Р. Линн, Р. Глейзер и Г. Борнштедт (редакторы), Оценка в переходный период: мониторинг национального прогресса в области образования (Справочные исследования, стр. 151–215). Стэнфорд, Калифорния: Национальная академия образования.
Стэнфорд, Калифорния: Национальная академия образования.
Hagarty, M., Mayer, R.E., & Monk, C.A. (1995). Понимание арифметических словесных задач: сравнение успешных и неудачных решателей задач. Журнал педагогической психологии , 87 , 18–32.
Хатано, Г. (1988, осень). Социальные и мотивационные основы математического понимания. Новые направления развития ребенка , 41 , 55–70.
Хиберт, Дж. (Ред.). (1986). Концептуальные и процедурные знания: пример математики . Хиллсдейл, Нью-Джерси: Эрлбаум.
Хиберт, Дж., И Карпентер, Т.П. (1992). Учиться и преподавать с пониманием. В Д. А. Гроуза (ред.), Справочник по исследованиям в области преподавания и обучения математике (стр. 65–97). Нью-Йорк: Макмиллан.
Хиберт, Дж., Карпентер, Т.П., Феннема, Э., Фусон, К.С., Вирн, Д., Мюррей, Х., Оливье, А., и Хумэн, П. (1997). Осмысление: преподавание и изучение математики с пониманием . Портсмут, Нью-Хэмпшир: Heinemann.
Портсмут, Нью-Хэмпшир: Heinemann.
Хиберт Дж. И Уирн Д. (1986). Процедуры над понятиями: приобретение знаний о десятичных числах.В J.Hiebert (Ed.), Концептуальные и процедурные знания: случай математики (стр. 199–223). Хиллсдейл, Нью-Джерси: Эрлбаум.
Хиберт Дж. И Уирн Д. (1996). Обучение, понимание и навыки сложения и вычитания многозначных чисел. Познание и обучение , 14 , 251–283.
Хилгард, Э. Р. (1957). Введение в психологию (2-е изд.). Нью-Йорк: Харкорт Брейс.
Инелдер, Б., И Пиаже Дж. (1958). Развитие логического мышления с детства до подросткового возраста . Нью-Йорк: Основные книги.
Катона, Г. (1940). Организация и запоминание . Нью-Йорк: издательство Колумбийского университета.
Килпатрик Дж. (1985). Заниматься математикой, не понимая ее: комментарий к Хигби и Кунихире. Психолог-педагог , 20 (2), 65–68.
Кнапп, М.С., Шилдс П.М. и Тернбулл Б.Дж. (1995). Академическая задача в классах с высоким уровнем бедности. Дельта Фи Каппан , 76 , 770–776.
Куба В.Л., Карпентер Т.П. и Сваффорд Дж. (1989). Количество и операции. В М. М. Линдквисте (ред.), Результаты четвертой математической оценки Национальной системы оценки успеваемости (стр. 64–93). Рестон, Вирджиния: Национальный совет учителей математики.
Стандартов для математической практики | Инициатива Common Core State Standards
Стандарты математической практики описывают различные виды знаний, которые преподаватели математики на всех уровнях должны стремиться развивать у своих учеников.Эти практики опираются на важные «процессы и навыки», которые имеют давнюю важность в математическом образовании. Первыми из них являются стандарты процесса NCTM для решения проблем, обоснования и доказательства, коммуникации, представления и связей. Вторые — это направления математической подготовки, указанные в отчете Национального исследовательского совета Adding It Up : адаптивное мышление, стратегическая компетентность, концептуальное понимание (понимание математических концепций, операций и отношений), беглость процедур (умение гибко выполнять процедуры, точно, эффективно и уместно) и продуктивному расположению (привычная склонность считать математику разумной, полезной и стоящей, в сочетании с верой в усердие и собственную эффективность).
Вторые — это направления математической подготовки, указанные в отчете Национального исследовательского совета Adding It Up : адаптивное мышление, стратегическая компетентность, концептуальное понимание (понимание математических концепций, операций и отношений), беглость процедур (умение гибко выполнять процедуры, точно, эффективно и уместно) и продуктивному расположению (привычная склонность считать математику разумной, полезной и стоящей, в сочетании с верой в усердие и собственную эффективность).
Стандарты в этой области:
CCSS.Math.Practice.MP1 Осознавайте проблемы и упорно решайте их.
Студенты со знанием математики начинают с объяснения себе значения проблемы и поиска точек входа для ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто предпринимают попытки решения. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной проблемы, чтобы получить представление о ее решении. Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графических данных и искать закономерности или тенденции. Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему.Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами.
Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графических данных и искать закономерности или тенденции. Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему.Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами.
CCSS.Math.Practice.MP2 Размышляйте абстрактно и количественно.
Учащиеся со знанием математики понимают величины и их отношения в проблемных ситуациях. Они привносят две взаимодополняющие способности для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентативными символами, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на своих референтов. — и возможность контекстуализировать , останавливаться по мере необходимости во время процесса манипуляции, чтобы исследовать референты для задействованных символов.Количественные рассуждения влекут за собой привычку создавать связное представление о рассматриваемой проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к тому, как их вычислить; знание и гибкое использование различных свойств операций и объектов.
Они привносят две взаимодополняющие способности для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентативными символами, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на своих референтов. — и возможность контекстуализировать , останавливаться по мере необходимости во время процесса манипуляции, чтобы исследовать референты для задействованных символов.Количественные рассуждения влекут за собой привычку создавать связное представление о рассматриваемой проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к тому, как их вычислить; знание и гибкое использование различных свойств операций и объектов.
CCSS.Math.Practice.MP3 Создавайте жизнеспособные аргументы и критикуйте рассуждения других.
Студенты со знанием математики понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они могут анализировать ситуации, разбивая их на случаи, распознавать и использовать контрпримеры. Они оправдывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и — если в аргументе есть изъян — объяснять, что это такое.Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних оценок. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они могут анализировать ситуации, разбивая их на случаи, распознавать и использовать контрпримеры. Они оправдывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и — если в аргументе есть изъян — объяснять, что это такое.Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних оценок. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS.Math.Practice.Модель MP4 с математикой.
Учащиеся со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах учащийся может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой.Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже. Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.
Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.
CCSS.Math.Practice.MP5 Стратегически используйте соответствующие инструменты.
Студенты, разбирающиеся в математике, рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Опытные студенты в достаточной степени знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как понимание, которое необходимо получить, так и их ограничения.Например, старшеклассники со знанием математики анализируют графики функций и решений, сгенерированные с помощью графического калькулятора.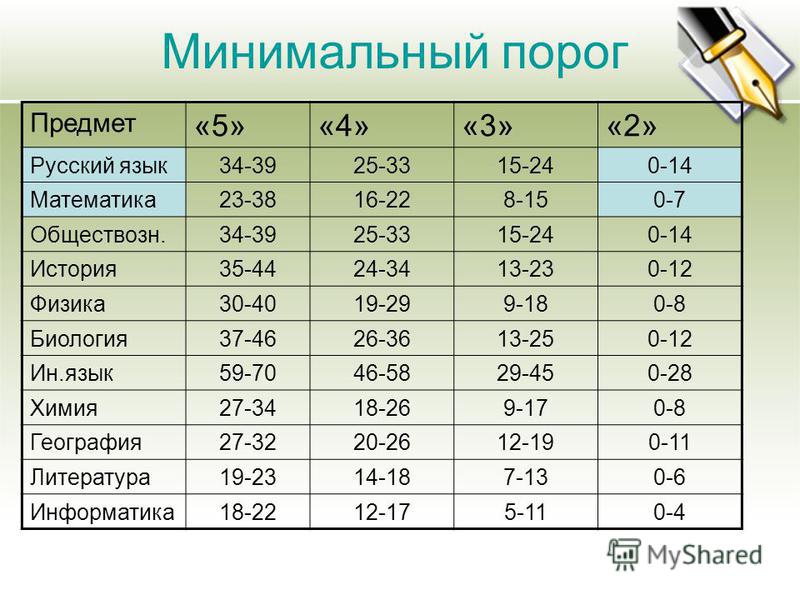 Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций.
Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций.
CCSS.Math.Practice.MP6 Внимание к точности.
Учащиеся со знанием математики стараются общаться с другими именно так. Они пытаются использовать четкие определения в обсуждениях с другими и в своих собственных рассуждениях. Они заявляют значение выбранных символов, в том числе используют знак равенства последовательно и надлежащим образом. Они осторожны при указании единиц измерения и маркировке осей, чтобы уточнить соответствие количеству в проблеме. Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.
Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.
CCSS.Math.Practice.MP7 Ищите и используйте структуру.
Учащиеся, разбирающиеся в математике, внимательно приглядываются, чтобы различить образец или структуру. Молодые студенты, например, могут заметить, что еще три и семь — это столько же, сколько еще семь и три, или они могут отсортировать набор фигур по количеству сторон у фигур.Позже учащиеся увидят, что 7 × 8 равно хорошо запоминающимся 7 × 5 + 7 × 3, при подготовке к изучению свойства распределения. В выражении x 2 + 9 x + 14 старшие ученики могут видеть 14 как 2 × 7 и 9 как 2 + 7. Они осознают значение существующей линии в геометрической фигуре и могут использовать стратегия рисования вспомогательной линии для решения задач. Они также могут сделать шаг назад для обзора и изменения перспективы. Они могут видеть сложные вещи, такие как некоторые алгебраические выражения, как отдельные объекты или как составленные из нескольких объектов.Например, они могут видеть 5-3 ( x — y ) 2 как 5 минус положительное число, умноженное на квадрат, и использовать это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y .
Они также могут сделать шаг назад для обзора и изменения перспективы. Они могут видеть сложные вещи, такие как некоторые алгебраические выражения, как отдельные объекты или как составленные из нескольких объектов.Например, они могут видеть 5-3 ( x — y ) 2 как 5 минус положительное число, умноженное на квадрат, и использовать это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y .
CCSS.Math.Practice.MP8 Ищите и выражайте закономерность в повторяющихся рассуждениях.
Студенты со знанием математики замечают, если вычисления повторяются, и ищут как общие методы, так и ярлыки. Ученики старших классов могут заметить при делении 25 на 11, что они повторяют одни и те же вычисления снова и снова, и прийти к выводу, что у них есть повторяющаяся десятичная дробь.Обращая внимание на расчет наклона, поскольку они неоднократно проверяют, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, ученики средней школы могут абстрагироваться от уравнения ( y — 2) / ( x — 1) = 3. Обратите внимание на закономерность в способе отмены терминов при раскрытии ( x — 1) ( x + 1), ( x — 1) ( x 2 + x + 1), и ( x — 1) ( x 3 + x 2 + x + 1) может привести их к общей формуле для суммы геометрического ряда.Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Обратите внимание на закономерность в способе отмены терминов при раскрытии ( x — 1) ( x + 1), ( x — 1) ( x 2 + x + 1), и ( x — 1) ( x 3 + x 2 + x + 1) может привести их к общей формуле для суммы геометрического ряда.Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Соединение стандартов математической практики со стандартами математического содержания
Стандарты математической практики описывают способы, с помощью которых развивающиеся студенты, практикующие математическую дисциплину, должны все активнее заниматься предметом по мере того, как они растут в математической зрелости и опыте на протяжении младших, средних и старших классов школы.Разработчики учебных программ, оценивания и повышения квалификации должны уделять внимание необходимости увязать математические практики с математическим содержанием в обучении по математике.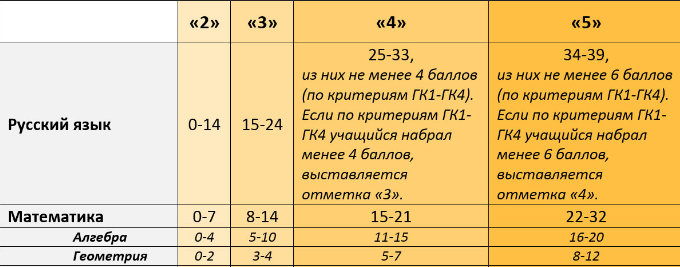
Стандарты математического содержания представляют собой сбалансированное сочетание процедуры и понимания. Ожидания, начинающиеся со слова «понять», часто являются особенно хорошей возможностью связать практики с содержанием. Студенты, которым не хватает понимания темы, могут слишком сильно полагаться на процедуры.Без гибкой основы для работы они с меньшей вероятностью будут рассматривать аналогичные проблемы, связно представлять проблемы, обосновывать выводы, применять математику к практическим ситуациям, осознанно использовать технологии для работы с математикой, точно объяснять математику другим ученикам, сделайте шаг назад, чтобы получить обзор, или отклонитесь от известной процедуры, чтобы найти ярлык. Короче говоря, непонимание фактически мешает ученику заниматься математической практикой.
В этом отношении те стандарты содержания, которые устанавливают ожидания понимания, являются потенциальными «точками пересечения» между Стандартами математического содержания и Стандартами математической практики. Эти точки пересечения призваны соотносить с центральными и генеративными концепциями школьной программы математики, которые в наибольшей степени заслуживают времени, ресурсов, инновационной энергии и концентрации, необходимых для качественного улучшения учебной программы, обучения, оценивания, профессионального развития и достижений учащихся математика.
Эти точки пересечения призваны соотносить с центральными и генеративными концепциями школьной программы математики, которые в наибольшей степени заслуживают времени, ресурсов, инновационной энергии и концентрации, необходимых для качественного улучшения учебной программы, обучения, оценивания, профессионального развития и достижений учащихся математика.
10 вещей, которые мы должны хотеть для всех наших студентов-математиков
Сью О’Коннелл, адаптировано из A Guide for Teachers , части ресурса Математика на практике .
Что значит хорошо разбираться в математике? Для многих из нас это было запоминание нашей математики, следование стандартному алгоритму и получение правильных ответов. Элементарная математика связана с памятью, скоростью и правильными ответами, верно? И если мы могли делать это, мы были вознаграждены хорошими оценками.
Но так ли это сегодня? Так мы должны думать об обучении математике, независимо от того, преподаем ли мы дистанционно или лично?
Сегодня наши ожидания от студентов выходят далеко за рамки способности запоминать математические факты и выполнять базовые вычисления. Хотя эти навыки важны, мы признаем их просто частью того, что нашим учащимся нужно знать и уметь. Мы ожидаем, что наши ученики будут понимать математику, думать математически и уметь использовать математику, которую они выучили.
Такое сочетание механических навыков и навыков мышления — не новая идея в преподавании. Читая, мы понимаем, что одни лишь базовые навыки не сделают вас читателем. Тот факт, что ученик хорошо владеет звуком и может называть слова, не означает, что он умеет читать. Сколько вы видели студентов, которые могут произносить слова, но не понимают, что они читают? Без понимания называть слова — это просто механический процесс.
Изучение фактов и процедур и надежда на то, что понимание происходит само по себе, имеет такой же смысл, как и обучение фонетике без внимания к пониманию. Результатом является приобретение механических навыков на очень слабой основе памяти и без особой надежды на применение. Мы хотим большего для наших студентов. Успеваемость наших студентов на международных тестах показывает, что они более опытны в вычислениях, чем в рассуждении, обосновании или решении проблем (Heibert, 2003), и что их успеваемость снижается, когда возникают более сложные ситуации.
Итак, если запоминание математических фактов и стандартных алгоритмов не делает математика, то каких навыков ему не хватает? Что мы хотим, чтобы наши студенты знали и могли делать, помимо процедурной беглости?
Вот 10 вещей, которые мы хотим, чтобы наши ученики принимали во внимание при планировании обучения:
Так много математики имеет смысл, когда вы понимаете большие идеи. Когда учащиеся понимают последовательность счета, значение числа, свойства и способы работы чисел, математика становится для них понятной.
Мы хотим, чтобы наши ученики разыгрывали ситуации, использовали конкретные объекты, рисовали картинки и диаграммы или использовали абстрактные символы для выражения математических идей. Моделирование математических идей подталкивает наших учеников к глубокому размышлению об идеях, дает им возможность показать свое понимание и обосновать свое мышление, а также позволяет им упростить математические задачи и решить математические задачи.
Мы хотим, чтобы наши ученики могли использовать свои математические знания для эффективного выполнения различных вычислений, включая вычисления с целыми числами, дробями и десятичными знаками.
Мы хотим, чтобы наши ученики развили четкое понимание чисел, которое позволяет им составлять или разлагать числа по мере необходимости, выполнять вычисления различными способами, понимать различные представления чисел, делать прогнозы, интерпретировать решения и понимать, когда решения имеют смысл.
Хотя мы по-прежнему ценим эффективные процедуры, мы хотим, чтобы наши студенты понимали, что они делают и почему это работает. Когда учащиеся изучают математические процедуры с помощью моделей и обсуждений, они не только имеют смысл, но и открывают для себя важные идеи о том, как работает математика.Вооруженные пониманием, учащиеся могут лучше применять свои знания в новых ситуациях или проблемах. Изучив сначала математические процедуры с помощью дискуссий и моделей расстановки ценностей, наши студенты создают прочную основу, которая впоследствии помогает им разобраться в стандартных алгоритмах.
Математика — это набор взаимосвязанных понятий и навыков, а не набор отдельных навыков. Видение связи между математическими идеями позволяет учащимся постоянно наращивать свои математические знания. По мере того, как наши студенты исследуют сложение, они связывают его с предыдущим опытом, полагаясь на.Изучая инструменты измерения, они думают о линиях с дробными числами, которые они создали. Изучая измерение площади, они снова размышляют об использовании массивов при умножении. Изучая десятичное вычитание, они связывают новую процедуру с известными процедурами вычитания целых чисел и сложения десятичных чисел. Взаимосвязь математических идей позволяет нашим ученикам опираться на предыдущие знания и делать важные выводы.
Видение связи между математическими идеями позволяет учащимся постоянно наращивать свои математические знания. По мере того, как наши студенты исследуют сложение, они связывают его с предыдущим опытом, полагаясь на.Изучая инструменты измерения, они думают о линиях с дробными числами, которые они создали. Изучая измерение площади, они снова размышляют об использовании массивов при умножении. Изучая десятичное вычитание, они связывают новую процедуру с известными процедурами вычитания целых чисел и сложения десятичных чисел. Взаимосвязь математических идей позволяет нашим ученикам опираться на предыдущие знания и делать важные выводы.
Мы хотим, чтобы наши ученики знали больше, чем , как складывать, вычитать, умножать и делить.Мы хотим, чтобы они могли применять математические навыки в реальных ситуациях. Мы хотим, чтобы они знали , когда нужно складывать, вычитать, умножать или делить. Мы хотим, чтобы у них был сильный набор навыков и стратегий, позволяющих решать сложные математические задачи.
Мы хотим, чтобы наши ученики рассуждали с помощью математических задач, анализировали данные, находили идеи, проверяли предположения и делали выводы.
Мы хотим, чтобы наши ученики могли точно объяснять свои стратегии, защищать свои ответы, описывать математические концепции, резюмировать свои выводы и объяснять свои выводы.Мы хотим, чтобы они рассказывали о математике в устной и письменной форме, чтобы обрабатывать свои идеи и совершенствовать собственное мышление, а также чтобы показать нам и другим то, что они знают.
Мы хотим, чтобы наши ученики были уверены в своих математических способностях, были готовы рисковать и упорно трудиться при выполнении сложных задач. Мы хотим, чтобы они любили математику!
♦ ♦ ♦ ♦
Сью О’Коннелл имеет многолетний опыт поддержки учителей в понимании математики и эффективном изменении способа преподавания.Бывшая учительница начальных классов, специалист по чтению и специалист по математике, она также является всемирно известным оратором и консультантом по образованию, который в настоящее время руководит организацией «Качественное развитие учителей», которая стремится обеспечить выдающееся профессиональное развитие математики для школ и районов по всей стране.
Руководящих вопросов по математическим задачам — возможности создания
Учителя постоянно стремятся задать правильные вопросы во время обучения.Существует прекрасный баланс между вопросом, который заставляет студентов задуматься, и вопросом, который содержит слишком много строительных лесов. Министерство образования пишет: «Исследователи поддерживают подход к решению проблем в классе математики, потому что он вовлекает студентов в расследование, побуждая их развивать и улучшать свои текущие знания, поскольку они« создают »объяснения, которые помогают им решить поставленную задачу. В конструктивистских классах студенты считаются теми, кто активно создает свои собственные знания.( Asking Effective Questions, июль 2011 г.) . Наша способность задавать вопросы нашим ученикам эффективно помогает нашим ученикам осознавать свои мыслительные процессы, устанавливать связи между идеями и концепциями и помогает им строить новое понимание.
Открытые математические задания предоставляют прекрасную возможность ответить на математические вопросы, которые побуждают учащихся глубже задуматься о концепции. Однако иногда в процессе выполнения задания мы обнаруживаем, что наши дети застревают. Они либо не знают, как подойти к проблеме, что делать дальше в решении проблемы, либо какие стратегии подходят для решения проблемы.Введите наводящие вопросы. Направляющие вопросы помогают ученикам обходить эти камни преткновения, не давая им слишком много информации. Они помогают укрепить уверенность учащихся в своих способностях, одновременно поддерживая их уровень. Направляющие вопросы помогают учащимся узнать, что ряд ответов, ответов и подходов принимаются и ценятся, что укрепит их уверенность в себе как изучающих математику и поможет им чувствовать себя более комфортно, рискуя или прося о помощи, когда это необходимо.
Вот 8 вещей, которые вам нужно запомнить, прежде чем задавать вопросы.
1. Предвидеть студенческое мышление
Предвидеть студенческое мышление
Планируя проблему или задачу, которую вы планируете использовать, попробуйте решить ее несколькими способами. Это поможет вам предугадать и предсказать, в каком направлении пойдут ваши ученики при решении этой проблемы. Это может помочь вам подготовиться к тому, чтобы объяснить учащемуся его мышление, помочь прояснить любые заблуждения и узнать, как и где вести обсуждение.
2. Ссылка на цели или задачи обучения
Перед тем, как начать урок, определите учебные цели или результаты, которых вы хотите достичь.Это поможет вам создавать задачи и задавать наводящие вопросы, которые помогут вашим ученикам сосредоточиться на желаемом результате.
3. Используйте открытые вопросы
Открытые вопросы полезны во многих отношениях. Во-первых, они поощряют и поддерживают различные подходы и способы решения задачи. Во-вторых, они помогают укрепить уверенность учащихся, поскольку позволяют каждому реагировать на своем уровне, используя свои собственные стратегии. Открытые вопросы автоматически различаются, потому что каждый студент будет использовать разные стратегии, решения или мыслительные процессы, соответствующие их текущему уровню.В-третьих, открытые вопросы сообщают каждому учащемуся, что ожидаемый и, что более важно, ценится диапазон ответов (в отличие от одного).
Открытые вопросы автоматически различаются, потому что каждый студент будет использовать разные стратегии, решения или мыслительные процессы, соответствующие их текущему уровню.В-третьих, открытые вопросы сообщают каждому учащемуся, что ожидаемый и, что более важно, ценится диапазон ответов (в отличие от одного).
4. Используйте вопросы, требующие точного ответа
Иногда становится легко задать риторические вопросы или вопросы типа «да / нет». Ни один из этих типов вопросов не подходит для совместного математического класса. Возьмем, к примеру, вопрос «Два плюс два — четыре, верно?». В этом вопросе нет нескольких точек входа и он сигнализирует о том, что ученик может что-то делать не так.Попробуйте что-нибудь вроде «Как можно сложить числа, чтобы получить четыре?». Это позволяет учащимся увидеть, что они могут подойти к проблеме разными способами.
5. Используйте вопросы, которые позволяют сотрудничать и разговаривать
Открытые вопросы — отличная отправная точка для математической беседы. Попросите учащихся поработать в парах или группах, чтобы обсудить свои идеи и решения. Затем попросите их обосновать или опровергнуть свою идею доказательствами. Это также прекрасное время, чтобы научить студентов уважительно оспаривать свои идеи и идеи своих одноклассников.Если учащиеся поймут, что ошибки являются обычным явлением в процессе обучения и что понимание темы является конечной целью, они будут более открыты для обсуждения своих идей и идей других.
Попросите учащихся поработать в парах или группах, чтобы обсудить свои идеи и решения. Затем попросите их обосновать или опровергнуть свою идею доказательствами. Это также прекрасное время, чтобы научить студентов уважительно оспаривать свои идеи и идеи своих одноклассников.Если учащиеся поймут, что ошибки являются обычным явлением в процессе обучения и что понимание темы является конечной целью, они будут более открыты для обсуждения своих идей и идей других.
6. Используйте высокоуровневые мыслительные глаголы
Использование глаголов из Таксономии Блума помогает учащимся глубже изучить тему и способствовать искреннему пониманию. Такие глаголы, как сравнивать, описывать, доказывать и показывать, могут быть мощными способами помочь студентам лучше понять тему.
7. Сохраняйте нейтральность в вопросах и языке тела
Наши студенты постоянно обращаются к нам за признаками правильного ответа. Они улавливают изменения в тоне нашего голоса, языке тела и выражении лица. Убедитесь, что ваши вопросы не являются осуждающими, и избегайте использования слов «правильно» / «неправильно», «правильно / неправильно» или «сложно / легко». Эти слова могут сигнализировать учащимся о том, что они сделали что-то неправильно.
Убедитесь, что ваши вопросы не являются осуждающими, и избегайте использования слов «правильно» / «неправильно», «правильно / неправильно» или «сложно / легко». Эти слова могут сигнализировать учащимся о том, что они сделали что-то неправильно.
8. Время ожидания имеет решающее значение
Предоставление учащимся времени ожидания после того, как они услышат или увидят вопрос, имеет решающее значение в их учебном процессе.Время ожидания может составлять от 3 до 10 секунд. Это не только дает учащимся возможность обрабатывать некоторую информацию, но также может помочь менее уверенным учащимся реагировать чаще и дает учащимся, которым необходимо поставить перед собой задачу, больше времени для поиска дополнительного решения. Выдержав приличное время ожидания, вы также можете использовать такие стратегии, как «Подумай-пара-поделись» или «Повернись и поговори», чтобы позволить учащимся обдумать свои мысли вслух.
Есть восемь основных категорий вопросов, которые вы можете задать своим ученикам. Решая, какие вопросы использовать, сначала посмотрите, с какими проблемами или камнями преткновения сталкиваются ваши ученики. Какова основная причина, по которой они не могут решить проблему или продолжить то, что начали? Это понимание поможет вам сформулировать лучшие вопросы для ваших учеников и направить их к конечной цели.
Решая, какие вопросы использовать, сначала посмотрите, с какими проблемами или камнями преткновения сталкиваются ваши ученики. Какова основная причина, по которой они не могут решить проблему или продолжить то, что начали? Это понимание поможет вам сформулировать лучшие вопросы для ваших учеников и направить их к конечной цели.
Некоторые из этих вопросов частично совпадают и могут использоваться в разных ситуациях. Они были отделены друг от друга только для того, чтобы уменьшить путаницу и оставаться организованными.
Наша цель как учителей — помочь нашим ученикам понять, как они думают и подходят к проблеме.То, как мы используем наводящие вопросы, поможет нашим ученикам увидеть связь между идеями в процессе работы над проблемой. Использование надежных наводящих вопросов во время выполнения математического задания действительно может помочь нашим ученикам улучшить свое концептуальное понимание и почувствовать себя более уверенными в своих математических способностях.
Получите БЕСПЛАТНУЮ копию вопросов здесь!
Принципы разработки математических задач, улучшающих имитационное и творческое мышление
Бергквист, Т., И Литнер Дж. (2012). Математические рассуждения в презентациях учителей. Journal of Mathematical Behavior, 31, , 252–269.
Артикул Google Scholar
Блэк П. и Вильям Д. (1998). Оценка и обучение в классе. Оценка в образовании: принципы, политика и практика, 5 (1), 7–74.
Артикул Google Scholar
Боулер, Дж.(2002). Опыт школьной математики: традиционные и реформаторские подходы к обучению и их влияние на мышление учащихся . Махва, Нью-Джерси: Лоуренс Эрлбаум.
Google Scholar
Боэсен, Дж., Хелениус, О., Литнер, Дж., Бергквист, Э., Бергквист, Т., Палм, Т., и Палмберг, Б. (2014). Развитие математической компетентности: от задуманного к принятому куррикулуму. Journal of Mathematical Behavior, 33 , 72–87.
Артикул Google Scholar
Боэсен, Дж., Литнер, Дж., И Палм, Т. (2010). Математическое обоснование, требуемое национальными тестами, и рассуждение, используемое студентами. Педагогические занятия по математике, 75 , 89–105.
Артикул Google Scholar
Брюссо, Г. (1997). Теория дидактических ситуаций по математике . Дордрехт: Kluwer Academic Publishers.
Google Scholar
Браун, А. Л. (1992). Дизайн экспериментов: теоретические и методологические проблемы в создании сложных вмешательств в условиях классной комнаты. Журнал обучающих наук, 2 (2), 141–178.
Артикул Google Scholar
Клементс, Д. Х., Уилсон, Д. К., и Сарама, Дж. (2004). Детское сочинение геометрических фигур: траектория обучения. Математическое мышление и обучение, 6 , 163–184.
Артикул Google Scholar
Кобб П., Конфри Дж., ДиСесса А., Лерер Р. и Шаубле Л. (2003). Дизайн экспериментов в образовательных исследованиях. Исследователь в области образования, 32 (1), 9–13.
Артикул Google Scholar
Коулз А. и Браун Л. (2016). Дизайн задач для способов работы: различия в преподавании и изучении математики. Журнал педагогического образования математики, 19 , 149–168.
Артикул Google Scholar
Данлоски, Дж., Роусон, К. А., Марш, Э. Дж., Натан, М. Дж., И Уиллингем, Д. Т. (2013). Улучшение обучения студентов с помощью эффективных методов обучения: перспективные направления когнитивной и педагогической психологии. Психологическая наука в интересах общества, 14 (1), 4–58.
Артикул Google Scholar
Вентилятор, Л., & Бохово, C. (2014). Переосмысление роли алгоритмов в школьной математике: концептуальная модель с акцентом на когнитивное развитие. ZDM – Международный журнал по математическому образованию, 46 , 481–492.
Артикул Google Scholar
Granberg, C., & Olsson, J. (2015). Решение проблем с использованием ИКТ и совместное творческое мышление: изучение линейных функций с использованием динамической математики. Journal of Mathematical Behavior, 37, , 48–62.
Артикул Google Scholar
Хэтти, Дж. (2009). Видимое обучение: синтез более 800 метаанализов, относящихся к достижению . Лондон: Рутледж.
Google Scholar
Хиберт, Дж. (2003). Что говорят исследования о стандартах NCTM. В J. Kilpatrick, G. Martin, & D. Schifter (Eds.), A Research companion to Principles and Standard for School Mathematics (pp.5–26). Рестон, Вирджиния: NCTM.
Google Scholar
Hiebert, J., & Grouws, D. (2007). Влияние преподавания математики в классе на учебу учащихся. В F. Lester (Ed.), Второй справочник исследований по преподаванию и изучению математики (стр. 1293–1312). Шарлотта, Северная Каролина: Издательство информационного века.
Google Scholar
Ядер, Дж., Литнер, Дж., И Сиденвалл Дж. (2015). Международный анализ учебников с акцентом на математические рассуждения — возможности учиться . В: J. Jäder, Elevers möjligheter till lärande av matematiska resonemang, Licentiate thesis, Linköping University, 2015.
Jonsson, B., Kulaksiz, YC. И Литнер, Дж. (2016) Творческое и алгоритмическое математическое рассуждение: эффекты обработки, соответствующей передаче, и упорной борьбы. Международный журнал математического образования в науке и технологиях .DOI: 10.1080 / 0020739X.2016.1192232.
Google Scholar
Йонссон, Б., Норквист, М., Лильеквист, Ю., и Литнер, Дж. (2014). Изучение математики с помощью алгоритмических и творческих рассуждений. Журнал математического поведения, 36 , 20–32.
Артикул Google Scholar
Карлссон, Л., Литнер, Дж., Йонссон, Б., Лильеквист, Ю., Норквист, М., и Нюберг, Л.(2015). Изучение математики без предлагаемого метода решения: длительное воздействие на производительность и мозговую активность. Тенденции в неврологии и образовании, 4 , 6–14.
Артикул Google Scholar
Килпатрик Дж., Сваффорд Дж. И Финделл Б. (2001). Суммируя: Помощь детям в изучении математики . Вашингтон, округ Колумбия: National Academy Press.
Google Scholar
Леунг, Ф.(2014). Чему мы можем и должны научиться из международных исследований достижений математики? Научно-исследовательский журнал математического образования, 26, , 579–605.
Артикул Google Scholar
Литнер, Дж. (2000). Математические рассуждения в школьных задачах. Образовательные исследования по математике, 41 (2), 165–190.
Артикул Google Scholar
Литнер, Дж.(2003). Математические рассуждения студентов в упражнениях по университетскому учебнику. Образовательные исследования по математике, 52 , 29–55.
Артикул Google Scholar
Литнер, Дж. (2004). Математические рассуждения в упражнениях из учебника математического анализа. Journal of Mathematical Behavior, 23, , 405–427.
Артикул Google Scholar
Литнер, Дж. (2008).Рамки исследования для творческих и имитационных рассуждений. Образовательные исследования по математике, 67 (3), 255–276.
Артикул Google Scholar
Маккенни С. и Ривз Т. (2012). Ведение учебного дизайна исследования . Лондон / Нью-Йорк: Рутледж.
Google Scholar
NCTM (2000). Принципы и стандарты школьной математики . Рестон, Вирджиния: Национальный совет учителей математики.
Google Scholar
Нисс, М. (2003). Математические компетенции и изучение математики: Датский проект КОМ. Третья средиземноморская конференция по математическому образованию, Афины , 115–124.
Нисс, М. (2007). Реакция на состояние и тенденции в исследованиях преподавания и обучения математике: Отсюда к утопии.В F. Lester (Ed.), Второй справочник исследований по преподаванию и изучению математики (стр. 1293–1312). Шарлотта, Северная Каролина: Издательство информационного века.
Google Scholar
Норквист, М. (2016). По математическим рассуждениям — Сказанное . Кандидатская диссертация, Университет Умео.
Олссон, Дж. (2017a). GeoGebra, совершенствование творческого математического мышления . Кандидатская диссертация, Университет Умео.
Олссон, Дж. (2017b). Вклад рассуждений в использование обратной связи от программного обеспечения при решении математических задач. Международный журнал естественно-математического образования . DOI: 10.1007 / s10763-016-9795-x (Предварительная онлайн-публикация) .
Google Scholar
Полиа, Г. (1954). Математика и правдоподобные рассуждения . Принстон, Н.Дж .: Princeton U.P.
Google Scholar
Рутвен, К., Лаборд, К., Лич, Дж., И Тибергин, А. (2009). Инструменты дизайна в дидактических исследованиях: инструменты эпистемологических и когнитивных аспектов дизайна обучающих последовательностей. Исследователь в области образования, 38 , 329–342.
Артикул Google Scholar
Schoenfeld, A. (1985). Решение математических задач .Орландо, Флорида: Academic Press.
Google Scholar
Шенфельд А. (2007). Метод. В F. Lester (Ed.), Второй справочник исследований по преподаванию и изучению математики (стр. 69–107). Шарлотта, Северная Каролина: Издательство информационного века.
Google Scholar
Шенфельд А. (2015). Мысли о масштабе. ZDM, 47 , 161–169.
Артикул Google Scholar
Щит, М., & Доул, С. (2013). Оценка потенциала учебников математики для содействия глубокому обучению. Образовательные исследования по математике, 82 , 183–199.
Артикул Google Scholar
Сиденвалл, Дж., Литнер, Дж., И Джедер, Дж. (2015). Рассуждения учащихся при решении задач из учебника математики. Международный журнал математического образования в науке и технологиях, 46 , 533–552.
Артикул Google Scholar
Серебро, E.(1997). Развитие творческих способностей с помощью инструкций, насыщенных решением математических задач и постановкой задач. ZDM – Международный журнал по математическому образованию, 29 (3), 75–80.
Артикул Google Scholar
Саймон М. (1995). Реконструкция математической педагогики с конструктивистской точки зрения. Журнал исследований в области математического образования, 26, , 114–145.
Артикул Google Scholar
Смит, М.С., и Штейн, М. К. (2011). Пять практик для организации продуктивных дискуссий по математике . Рестон, Вирджиния: Национальный совет учителей математики.
Google Scholar
Шрираман Б., Хаавольд П. и Ли К. (2013). Математическое творчество и одаренность: комментарий и обзор теории. ZDM – Международный журнал по математическому образованию, 45 (2), 215–225.
Артикул Google Scholar
Стейси, К., И Винсент Дж. (2009). Способы рассуждения в объяснениях в австралийских учебниках математики для восьмых классов. Образовательные исследования по математике, 3 , 271–288.
Артикул Google Scholar
Стар, Дж. Р. (2005). Переосмысление процедурных знаний. Журнал исследований в области математического образования, 36 , 404–411.
Google Scholar
Steigler, J., И Хиберт, Дж. (1999). Пробелы в обучении . Нью-Йорк, Нью-Йорк: Свободная пресса.
Google Scholar
Штейн, М. К., Энгл, Р. А., Смит, М. С., и Хьюз, Е. К. (2008). Организация продуктивных математических дискуссий: пять практик, которые помогут учителям выйти за рамки шоу и рассказа. Математическое мышление и обучение, 10 , 313–340.
Артикул Google Scholar
Штейн, М.К., Гровер, Б. В., и Хеннингсен, М. (1996). Развитие способности студентов к математическому мышлению и рассуждению. Американский журнал исследований в области образования, 33 , 455–488.
Артикул Google Scholar
Свон, М. (2008). Разработка опыта обучения множественным представлениям по вторичной алгебре. Образовательный дизайнер, 1 , 1–17.
Google Scholar
Томпсон, Д., Сенк, С., и Джонсон, Г. (2012). Возможность научиться рассуждать и доказывать в учебниках математики для старших классов. Журнал исследований в области математического образования, 43 , 253–295.
Артикул Google Scholar
Ван ден Аккер, Дж. (2010). Наведение мостов: как исследования могут улучшить политику в отношении учебных программ и практику в классе. В С. Стоуни (ред.), После Лиссабона 2010: Перспективы исследований и разработок для образовательной политики в Европе Европа (Ежегодник CIDREE 2010) (стр. 175–196).Слау: NFER.
Google Scholar
Ван Стинбругге, Х. и Норквист, М. (2016). Разгадывать рассуждения студентов: анализировать обсуждения в малых группах во время решения задач. В М. Норквист (ред.), О математических рассуждениях — Сказанное или обнаружение . Кандидатская диссертация, Университет Умео.
В математике вы должны помнить …
В математике вы должны помнить …США намного хуже, чем большинство наших экономических конкурентов, по успеваемости школьников по математике. Было сделано много попыток улучшить эту мрачную производительность, но ни одна из них не сработала. На мой взгляд (и я далеко не один так думаю), причина ясна. Все эти попытки были направлены на улучшение базовых математических навыков. Напротив, акцент должен быть на другом.
Математика — это способ размышления о проблемах и проблемах мира.Получите правильное мышление, и навыки приходят в основном бесплатно.
Многочисленные исследования за последние тридцать лет показали, что, когда люди любого возраста и любого уровня способностей сталкиваются с математическими проблемами, которые возникают естественным образом в реальном контексте, имеющем для них значение, и где результат имеет для них непосредственное значение, они быстро достичь высокого уровня компетенции. Как высоко? Обычно 98 процентов, вот насколько высока. Я описываю некоторые из этих исследований в своей книге Математический ген (Basic Books, 2000).Я также объясняю, почему те же самые люди, когда они сталкиваются с одними и теми же математическими задачами в традиционном классе с бумагой и карандашом, показывают результаты на низком уровне 37 процентов.
Доказательства очевидны. Дело не в том, что люди не могут мыслить математически. Дело в том, что у них огромные проблемы с тем, чтобы делать это в отвлеченной от контекста абстрактной обстановке.
Так почему же мы по-прежнему уделяем внимание навыкам? Поскольку многие люди, даже те, кто находится у власти и влияния, не только совершенно не осведомлены о результатах, которые я только что упомянул, они даже не понимают, что такое математика и как она работает.Все, что они видят, — это навыки, и они ошибочно думают, что в этом и состоит математика. Учитывая, что для большинства людей их последним близким знакомством с математикой был школьный урок математики на основе навыков, нетрудно понять, как возникает это заблуждение. Но путать математику с овладением навыками — все равно что думать, что архитектура — это кладка кирпича или смешение музыки с овладением музыкальной гаммой.
Конечно, базовые навыки важны. Но они всего лишь инструменты математического мышления.В докомпьютерную эпоху индустриальному обществу, подобному Соединенным Штатам, требовалась большая рабочая сила, состоящая из людей с базовыми математическими навыками, которые могли бы выполнять задания, порученные им другими. Но на сегодняшнем рабочем месте монета царства — творческое решение проблем, обычно в совместных группах, с использованием математического мышления, когда это необходимо. Насколько хорошо мы готовим сегодняшних студентов к жизни в этой среде? Как нас сравнивать с нашими странами-конкурентами?
Ответ — не очень.В ходе международного опроса, проведенного в 2003 году, студентов из сорока стран спросили, согласны они или не согласны с утверждением: «Когда я изучаю математику, я стараюсь выучить ответы на задачи наизусть». Среди всех учащихся в среднем 65 процентов не согласились с этим утверждением — что обнадеживает, поскольку это безнадежный способ изучения математики, — но 67 процентов американских детей согласились с ним! [Обучение для завтрашнего мира: первые результаты исследования PISA 2003, ОЭСР]
Так что мы делаем не так?
Люди расходятся во мнениях по некоторым деталям, но, похоже, существует широкий (хотя и не универсальный) консенсус по трем основным причинам:
- Наша учебная программа по математике (на самом деле, это учебная программа, поскольку в каждом штате свои собственные, но жалоба распространяется на все) содержит слишком много обязательных тем, каждую из которых можно преподавать только с небольшой степенью — часто называемой проблема «шириной в милю, глубиной в дюйм»;
- Слишком много учителей математики плохо разбираются в предмете, который они преподают;
- В большинстве классов математика преподается в жесткой форме, основанной на правилах.
В первой сцене, которая является наиболее распространенной, вы увидите учеников, сидящих аккуратно организованными рядами лицом к учителю, стоящему впереди. На столе перед каждым учеником вы, вероятно, увидите учебник, тетрадь, ручку или карандаш и, возможно, калькулятор.В начале каждого урока учитель проводит некоторое время у доски, объясняя какое-то новое правило или методику и работая с одним или двумя примерами. Затем ученики откроют свои учебники и приступят к работе с рядом заданных примеров, решения которых требуют техники, которую им только что показали. По большей части они будут работать в одиночестве и в тишине. Когда они сталкиваются с проблемой, они обращаются за помощью к учителю, а не друг к другу. Когда они выполнили задание, цикл начинается заново.Этот метод обучения широко известен как «традиционный подход». Это подходящее название, поскольку оно использовалось с самого начала математики, около трех тысяч лет назад.
Другая, менее распространенная сцена выглядит гораздо более хаотичной. Группы студентов сидят вокруг круглых столов, обсуждая, как решить конкретную проблему, или стоят у доски, обсуждая, как лучше всего действовать. Учитель ходит по комнате, по очереди разговаривая с разными группами, предлагая дальнейшие действия или указывая на возможные ошибки в определенной линии рассуждений, которой следуют ученики.Иногда учитель призывает всю группу к порядку и просит одну группу объяснить свое решение остальному классу или прочитать короткую мини-лекцию о конкретной концепции или методе. Иногда это называют «прогрессивным подходом».
Вопрос о том, какой метод лучше, лежит в основе печально известных «математических войн», которые бушевали в Калифорнии и Нью-Йорке (в частности). Хотя во многих странах можно найти одни и те же два педагогических подхода, только в США этот вопрос стал предметом ожесточенных и часто ожесточенных дебатов.Как аутсайдер, приехавший из Великобритании довольно поздно в моей карьере, меня с самого начала поразило то, что большая часть дебатов касалась создания и уничтожения соломенных людей. Учителей-традиционалистов обвиняли в том, что они не делали ничего, кроме безжалостного обучения своих учеников базовым процедурным навыкам, не обращая внимания на развитие математических понятий, в то время как прогрессивных учеников сжигали бы в виде чучела за то, что они не ценят базовые навыки (или видят необходимость их практиковать). и подарить студентам жидкую, разбавленную кашицу, в которой не было математической основы.Несомненно, вы можете найти примеры каждого из них, но по большей части эти карикатуры существуют только в умах критиков, которые делают эти утверждения, и ни один из них не является верным. Скорее, вы обнаружите, что тысячи учителей делают все, что в их силах, пытаясь сбалансировать потребность в концептуальном понимании с необходимостью практиковать базовые навыки, но не уверены в том, как лучше всего поступить, особенно когда дело доходит до мотивации своих учеников. . Между тем, в отсутствие каких-либо четких доказательств того, как лучше поступить, большинство учителей по вполне понятным причинам отказываются от более или менее тех же методов обучения, что и сами испытали.В подавляющем большинстве это традиционный метод, хотя тот факт, что никто не смог заставить этот подход работать (для большинства студентов) за три тысячи лет, заставляет задуматься, есть ли лучший способ.
Теперь, наконец, есть свидетельства, и их собирают еще больше. Это означает, что грубая вера и слепая вера, наконец, могут начать заменяться аргументированным выбором, основанным на доказательствах. Это обязательно произойдет, но еще неизвестно, сколько времени это займет после такой ожесточенной битвы.Скорее всего, конфликт будет полностью прекращен только после того, как то же самое произойдет с некоторыми из наиболее видных сторонников. Между тем, ожидайте постепенных изменений по мере того, как все больше учителей, родителей и политиков узнают о растущей массе достоверных данных.
Одной из исследователей, которая терпеливо собирала эти данные, является Джо Булер, и она недавно опубликовала краткое и удобочитаемое резюме некоторых своих открытий в виде книги: При чем тут математика? Хотя книга Боулера написана для родителей, я считаю, что ее следует читать всем, кто занимается математическим образованием.Вы можете усомниться в некоторых ее выводах. Действительно, некоторые так и поступили, когда ее работа впервые стала известна в США, примерно в 2003 году, хотя ее последующие исследования, на мой взгляд, дали ответы на некоторые из поднятых вопросов. Но в такой области, как математическое образование, где так трудно получить убедительные убедительные доказательства и где большинство утверждений об эффективности различных педагогических методик основаны не более чем на экстраполяции личного опыта (учителя, а не студент), любое углубленное исследование, подобное ее, заслуживает серьезного рассмотрения.Хотя бы потому, что Боалер сосредотачивает свое внимание не на учителях, а на обучаемых учениках. Ее недавняя книга легла в основу оставшейся части этого эссе. Цену, которую я взял в качестве названия, можно найти на странице 40.
Боулер начала свою карьеру учителем математики в своей родной Великобритании, затем перешла в академические круги (Лондонский университет) и в течение нескольких лет была профессором математического образования (и, следовательно, моим коллегой) в Стэнфорде. Затем, в 2006 году, она вернулась в Великобританию, чтобы занять недавно созданную кафедру математического образования Марии Кюри в Университете Сассекса в Англии. Этим летом она возвращается в Стэнфорд, где мы очень хотим ее вернуть.
На протяжении многих лет Боалер проводил интервью с сотнями студентов как из классов с традиционным преподаванием математики, так и с теми, кто придерживался более прогрессивного подхода. Один из вопросов она задала им, что нужно, чтобы добиться успеха в математике. Безусловно, наиболее частый ответ, который она получала от студентов, обучаемых традиционным способом, — это обратить особое внимание .
Среди других ответов, которые Болер получила в школах с традиционной педагогикой, которые она цитирует в своей книге, — [стр.41]:
«Меня просто не интересует, во-первых, вы даете мне формулу, я должен запомнить ответ, применить его, и все».
«Вы должны быть готовы признать, что иногда вещи выглядят не так — они не видят, что вы должны их делать. Как будто в них есть смысл. Но вы должны их принять».
Другая ученица с традиционным обучением, которую опрашивал Болер, по имени Ребекка, была добросовестной, целеустремленной и умной и регулярно получала оценки A + по математике.Она смогла следовать методам, продемонстрированным ее учителем в классе, и могла идеально их воспроизвести. Но она не понимала, что делает, и в результате считала себя плохой в математике. Когда Болер спросил ее, почему она так думает, она ответила: «Потому что я плохо помню вещи, а нужно так много вспомнить». [стр.164.]
Школа у трасс
В течение четырех лет Болер следил за успехами семисот учеников в трех средних школах.Одним из трех был «Railside High». Не настоящее название, эта школа находилась в городе, рядом с железнодорожной веткой. Впервые она посетила школу в 1999 году, услышав, что они, похоже, достигают замечательных результатов, несмотря на плохое расположение и ветхий вид школьных зданий.Ряд особенностей выделили Railside. Во-первых, студенты были совершенно не отслежены, и все изучали алгебру в качестве первого курса, а не только студенты с более высокими достижениями.Во-вторых, вместо обучения ряду методов, таких как факторизация многочленов или решение неравенств, школа организовала учебную программу вокруг более крупных тем, таких как «Что такое линейная функция?». Студенты научились использовать различные виды представлений, слов, диаграмм, символов таблиц, объектов и графиков. Они работали вместе в группах со смешанными способностями, при этом более успешные сотрудники сотрудничали с более низкими исполнителями, и от них ожидали и поощряли объяснять свою работу друг другу.[стр.58-68]
Родители, чье собственное математическое образование было более традиционным, когда ученики сидели рядами в классах с потоком способностей, учителя показывали им методы, а затем молча работали самостоятельно — а это практически все родители — часто не могут поверить в то, что подход Railside может сработать. Они считают, что из-за неплотной структуры дети не овладеют навыками достаточно хорошо, чтобы пройти тесты, и что присутствие более слабых учеников потянет за собой лучших.Часто они сохраняют это убеждение, несмотря на то, что они открыто признают, что традиционный подход им не подходит, и вопреки их собственному опыту повседневной работы, когда за многие годы они узнали, что совместная работа очень эффективна и что когда кто-то, кто умеет что-то делать, помогает тому, кто не умеет, и учатся, и извлекают пользу из этого опыта.
В девятнадцатом веке и на протяжении большей части двадцатого большинство промышленных рабочих выполняли бесшумную работу самостоятельно, в больших открытых офисах или на производственных линиях под наблюдением менеджера.Школы, которые всегда предназначались для подготовки детей к взрослой жизни, имели аналогичную структуру. Важным жизненным уроком было уметь следовать правилам и думать внутри коробки. Но сегодняшний мир совсем другой — по крайней мере, для тех из нас, кто живет в высокоразвитых обществах. Компании давно приняли новые, более совместные методы работы, где творческое решение проблем является ключом к успеху — те, которые не прекратили свое существование, — но в целом школы еще не осознали, что им нужно измениться и начать работать аналогичным образом.
Конечно, в школах может быть иначе, как думают многие родители. В конце концов, они будут спорить, что то, что работает для взрослых, может не быть успешным для детей. Это справедливое беспокойство. Эта проблема решается сразу после открытия Боулера. Две другие школы, которые изучал Боулер вместе с Рэйлсайд, находились в более богатых пригородных районах, и ученики начинали с более высокими достижениями по математике, чем те, что были в городской школе Рэйлсайд.Поскольку в этих двух школах была принята традиционная форма обучения, Болер смог сравнить результаты учащихся за все четыре года обучения в средней школе. К концу первого года она обнаружила, что ученики Рэйлсайда достигли того же уровня, что и студенты из пригорода, на тестах по алгебре. К концу второго года ученики Railside опережали своих сверстников из двух пригородных школ как по алгебре, так и по геометрии. К старшему году обучения 41 процент учеников Рэйлсайда учились в продвинутых классах предварительного вычисления и математического анализа, по сравнению с только 23 процентами учеников двух других школ в более богатых районах.
Более того, студенты Railside научились получать удовольствие от математики и считали ее полезной. Когда Болер и ее команда опросили 105 учеников (в основном старшеклассников) об их планах на будущее, 95 процентов учеников двух пригородных школ заявили, что не собираются продолжать заниматься математикой как предметом, даже те, кто добился успеха. В Railside 39% заявили, что планируют продолжить обучение на математических курсах.
Когда Боулер посещал класс, где преподавали в стиле Railside, и спрашивал студентов, над чем они работают, они описывали проблему и как они пытались ее решить.Когда она задавала те же вопросы студентам, которых обучали традиционным способом, они обычно говорили им, на какой странице книги они находились. Когда она спросила их: «Но что вы на самом деле делаете?» они бы ответили: «О, я делаю номер 3». [стр.98]
Британцы совершают ту же ошибку
До поступления в Стэнфорд, когда она все еще работала в своей родной Великобритании, Болер начала аналогичное продольное исследование, сравнивая две очень разные школы, которые она назвала Феникс-Парк (в районе рабочего класса) и Эмбер-Хилл (расположенный в более зажиточном районе). район).Первый использовал совместный, проектный подход, аналогичный Railside, второй — более традиционную педагогику. [стр.69-83]Боулер выбрал эти две школы, потому что, несмотря на то, что они находятся в разных социальных регионах, их набор учеников был демографически очень похожим, все поступающие ученики в возрасте тринадцати лет все испытали одинаковый образовательный подход, а учителя в обеих школах были высококвалифицированными.
Одно различие между английскими школами и школами в Калифорнии состоит в том, что Великобритания не следует идиотской американской практике разделения математики на отдельные суб-предметы, такие как алгебра I, алгебра II или геометрия; скорее они просто изучают математику (или «математику», как ее называют в Британии).Но в остальном это было очень похоже на исследование, которое она впоследствии проводила в Калифорнии, и результаты были поразительно похожими.
В Феникс-парке ученикам была предоставлена значительная свобода на уроках математики. Обычно им давали выбор между различными проектами, над которыми они могли работать, и их поощряли определять характер и направление своей работы. Один студент объяснил Боулеру, как они работали с этими словами: [стр.70]
«Обычно мы сначала ставим задачу и нас учат навыкам, необходимым для ее выполнения, а затем мы продолжаем выполнение задачи и просим учителя о помощи.»
Другой описал процесс так: [стр.70]
«Вы просто ставите задачу, а затем приступаете к ней … вы исследуете разные вещи, и они помогают вам в этом … так что разные навыки как бы приспособлены для разных задач».
В одном задании, которое описывает Боалер, студентам просто сказали, что у определенного объекта есть объем 216, и попросили описать, как он может выглядеть.В другом случае ученикам сказали, что у одного фермера есть ограждения длиной тридцать шесть метров, и попросили найти самую большую площадь, которую они могут ограждать.
Если вы думаете, что это «поверхностно» или «ненастоящая математика», то почти наверняка вы живы, и это ходячее доказательство того, что традиционные инструкции по математике убивают разум, чтобы увидеть множество возможностей, которые предлагает каждая задача, и количество математического мышления, необходимое для выполнения. из расследований. В своей книге Боулер описывает некоторые творческие идеи, которые студенты Феникс-Парка привнесли в выполнение этих двух заданий, и результаты обучения математике.На мой взгляд, то, что она описывает, — это раннее развитие творческих, совместных навыков решения проблем, которые необходимы в современном мире. Как объяснил ей один студент: [стр.74]
«Если вы найдете правило или метод, вы попытаетесь приспособить их к другим вещам».
В то время как ученики Феникс-парка открывали для себя, что математика — это сложная и увлекательная задача, обеспечивающая отличный выход для их естественного человеческого любопытства, в Эмбер-Хилле дела шли совсем иначе.Там студенты много работали, но большинство из них не любили математику. Они пришли к выводу, что математика — это предмет, требующий только запоминания правил и процедур. Как сказал один студент: [стр.75]
«В математике есть определенная формула, к которой нужно добраться, скажем, от A до B, и нет другого способа получить ее. Или, может быть, есть, но вы должны запомнить формулу, вы должны ее запомнить . »
Именно в Эмбер-Хилл студент предоставил Боулеру цитату, которая составляет заголовок колонки в этом месяце.
Хотя ученики Эмбер Хилл тратили больше времени на выполнение заданий, чем их сверстники в Феникс-парке, они думали, что математика — это набор правил, которые нужно запоминать. Те, кто добились успеха, сделали это не благодаря пониманию математических идей, а благодаря тому, что научились следовать подсказкам. Самым важным сигналом, подсказывающим им, как решить проблему, был метод, который учитель только что объяснил на доске, или рабочий пример, который непосредственно предшествовал этому в учебнике. Еще одна подсказка заключалась в том, чтобы использовать всю информацию, содержащуюся в вопросе, но ничего больше.
Эту стратегию можно заставить работать до тех пор, пока не будет проведено обследование в конце года, когда эти подсказки не появятся. Как и следовало ожидать, даже те студенты Amber Hill, которые хорошо успели в течение семестра, плохо сдали эти экзамены. И в национальных экзаменах, которые все британские студенты сдают в возрасте шестнадцати лет, ученики Феникс-Парка легко превзошли их. Столкнувшись с проблемой, которую они не осознавали как нечто знакомой, ученик Эмбер-Хилл мог замерзнуть или тщетно пытаться запомнить правильную формулу, тогда как ученики Парка Феникс пытались понять ее и адаптировать метод, который, по их мнению, мог заставить работать.
Помимо занятий в двух школах, Болер также взяла интервью у учеников о том, как они используют математику вне школы. К тому времени многие из них работали по выходным. Все сорок учеников Эмбер Хилл, у которых она брала интервью, заявили, что они никогда, никогда не будут использовать методы, полученные в школе, в любой ситуации за пределами школы. Для них то, чему их учили в классе математики, было странным кодом, который можно использовать только в одном месте — в классе математики.Напротив, ученики Феникс-Парка были уверены, что воспользуются методами, которым они научились в школе, и привели ей примеры того, как они уже использовали изученную в школе математику на своей работе на выходных.
В последующем исследовании, которое она провела несколько лет спустя, Болер опросила 24-летних выпускников школ Феникс-Парк и Эмбер-Хилл. Когда они учились в школе, их социальный класс, определяемый работой их родителей, был одинаковым в обеих школах.Но восемь лет спустя молодые люди из Феникс-Парка работали на более высококвалифицированных или профессиональных должностях, чем взрослые из Эмбер-Хилл. Демонстрируя, как хорошее образование может привести к восходящей социальной мобильности, 65 процентов взрослых в Феникс-парке работали более профессионально, чем их родители, по сравнению с 23 процентами взрослых в Эмбер-Хилл. Фактически, 52 процента взрослых в Эмбер Хилл работали на меньше, чем на профессиональных должностях, чем их родители, по сравнению с только 15 процентами выпускников Феникс-Парка.[стр.80-83]
Конечно, вы не получите эту информацию, прочитав компьютерные результаты стандартизированных тестов, столь любимых системой образования США. Булер не находит свои данные, глядя на экран компьютера. Она выходит и говорит с людьми, о которых идет речь: о студентах и тех, кто был студентами. Я спрашиваю вас, какая информация более важна: результат стандартного письменного теста, сданного в конце учебного эпизода, или влияние, которое этот учебный эпизод оказал на заинтересованного человека? Какое утверждение доставит вам больше удовольствия как родителю (если вы один) ?:
- «Благодаря хорошему обучению мой ребенок набрал 79% на последнем тесте по математике» или
- «Благодаря хорошему обучению мой ребенок имеет гораздо лучшую работу и ведет гораздо более интересную и полезную жизнь, чем я.»
Если вы хотите узнать больше об исследованиях Болер, см. Ее книгу, которую я цитировал, и ее предыдущую книгу, отмеченную наградами. Опыт школьной математики.
Что тестировалось в разделе SAT Math? Темы и практика
Вашим первым шагом в подготовке к математическому разделу SAT должно быть знакомство с тем, что на нем написано.Какой бы класс математики вы ни брали в школе, вы должны быть в состоянии покорить математические темы SAT с правильным подходом к подготовке к экзаменам. Давайте начнем это руководство с обзора общего формата математической части теста SAT.
Формат SAT Math
Математика будет вашим третьим и четвертым разделами на SAT, сразу после чтения, письма и языка. Сначала вы получите 25-минутный раздел , в течение которого вы не можете использовать калькулятор. После небольшого перерыва вы перейдете к 55-минутному участку .В этом более длинном разделе вам разрешено пользоваться калькулятором.
Оба раздела начинаются с вопросов с несколькими вариантами ответов, каждый из которых содержит четыре варианта ответа. Затем вас попросят дать несколько ответов учащихся, более известных как «сетки». В разделе калькулятора некоторые из этих таблиц будут связаны друг с другом как часть вопроса Extended Thinking.
Вот разбивка времени, количества вопросов и типов вопросов по двум разделам SAT по математике.
| Раздел | Количество вопросов | Время |
|
Без калькулятора |
15 вариантов выбора, 5 элементов сетки | 25 минут |
| Калькулятор | 30 вариантов выбора, 8 таблиц (включая один вопрос на расширенное мышление) | 55 минут |
| Итого | 58 вопросов | 80 минут |
Хотя вы можете использовать калькулятор только в более длинном математическом разделе, у вас будет доступ к следующей справочной информации для геометрии в обоих разделах:
Конечно, вам лучше запомнить эту информацию, чем тратить время на то, чтобы пролистывать тестовый буклет обратно к этим формулам.На самом деле этот материал не так уж и важен для математической секции, поскольку геометрические задачи составляют менее 10% вопросов. При этом, какие навыки и концепции наиболее распространены в математическом разделе?
Контент — король! Или, по крайней мере, очень важно освоить, прежде чем сдавать SAT.
Темы SAT по математике
Хотя математический раздел не уделяет большого внимания задачам геометрии, он фокусируется на алгебре, решении уравнений и интерпретации данных из таблиц и графиков.College Board разделяет типы вопросов на три основные категории: Сердце алгебры, Паспорт для продвинутой математики и Решение проблем и анализ данных (они, очевидно, отказались от творческого наименования, когда достигли третьей категории).
Эти три области описывают около 90% математических вопросов SAT. Остальные 10% называются просто Дополнительные темы , и они в основном включают геометрию, базовую тригонометрию и комплексные числа.
Давайте подробнее рассмотрим каждую из этих категорий, пройдя по темам SAT по математике и навыкам, которые они проверяют.После описания каждого из них вы увидите три официальных образца практических вопросов от College Board.
Сердце алгебры
вопросов SAT по математике в категории «Сердце алгебры» относятся к линейным уравнениям, неравенствам, функциям и графикам.
Ниже приведены официальные темы, определенные Советом колледжей, а также краткое изложение задач, к которым вы должны быть готовы, чтобы ответить на эти вопросы, и некоторые примеры проблем.
Официальные темы
- Решение линейных уравнений и линейных неравенств (в этих выражениях x — константа или произведение константы)
- Интерпретация линейных функций
- Задачи о линейных неравенствах и уравнениях
- Построение графиков линейных уравнений
- Задачи о линейных функциональных словах
- Системы словесных задач линейных неравенств
- Решение систем линейных уравнений
Сводка задач
- Используйте несколько шагов, чтобы упростить выражение или уравнение или решить для переменной.
- Найдите переменную в функциях или системах неравенств с двумя переменными (обычно x и y).
- Определите, входит ли данная точка в набор решений или при каком значении выражение не имеет решения.
- Выберите график, показывающий алгебраическое уравнение, или, с другой стороны, выберите уравнение, описывающее график.
- Укажите, как на график повлияет данное изменение его уравнения.
Примеры вопросов
Решение систем линейных уравнений:
Решение систем линейных неравенств:
Построение линейного уравнения:
Возьмите свой паспорт — мы пересекаем границу в страну продвинутой математики.
Паспорт для углубленного изучения математики
В то время как вопросы Heart of Algebra сосредоточены на линейных уравнениях, вопросы Passport to Advanced Math относятся к нелинейным выражениям или выражениям, в которых переменная возведена в степень, отличную от нуля или единицы. Эти вопросы предложат вам работать с квадратными уравнениями, экспоненциальными выражениями и задачами со словами.
Читайте полный список тем, относящихся к разделу «Паспорт для углубленного изучения математики», за которым следует краткое изложение задач и три примера вопросов SAT.
Официальные темы
- Решение квадратных уравнений
- Интерпретация нелинейных выражений
- Квадратичные и экспоненциальные задачи со словами
- Радикалы и рациональные показатели
- Операции с рациональными выражениями и многочленами
- Полиномиальные множители и графики
- Графики нелинейных уравнений
- Линейные и квадратичные системы
- Структура в выражениях
- Изолирующие количества
- Функции
Сводка задач
- Решите уравнения, разложив на множители или используя другие методы, чтобы переписать их в другой форме.
- Сложите, вычтите, умножьте или разделите два рациональных выражения или разделите два полиномиальных выражения и упростите свои результаты.
- Выберите график, соответствующий нелинейному уравнению, или уравнение, которое соответствует графику.
- Определите уравнение кривой из описания графика.
- Выясните, как изменится график, если его уравнение изменится.
Примеры вопросов
Функции:
Нелинейных выражений:
Графики нелинейных уравнений:
Решение проблем и анализ данных
Эта третья и последняя основная категория включает вопросы, которые просят вас работать с коэффициентами, отношениями, процентами и данными из графиков и таблиц. Прочтите официальные темы, краткое изложение задач и три типовых вопроса.
Официальные темы
- Соотношения, пропорции и пропорции
- процентов
- Шт.
- Данные таблицы
- Диаграммы рассеяния
- Основные характеристики графиков
- Линейно-экспоненциальный рост
- Вывод данных
- Центр, распространение и форма распределений
- Сбор данных и выводы
Сводка задач
- Решайте многоэтапные задачи для расчета соотношения, нормы, процента, единицы нормы или плотности.
- Используйте заданное соотношение, норму, процент, удельную норму или плотность для решения многоступенчатой задачи.
- Выберите уравнение, которое лучше всего соответствует диаграмме рассеяния.
- Используйте таблицы для обобщения данных, например вероятностей.
- Оцените совокупность на основе выборочных данных.
- Используйте статистику для определения среднего значения, медианы, режима, диапазона и / или стандартного отклонения.
- Оцените таблицы, графики или текстовые сводки.
- Определите точность метода сбора данных.
Примеры вопросов
Расчет данных по ставке:
Диаграмма рассеяния и коэффициент расчета:
Расчет процента на основе данных таблицы:
Следующие несколько категорий не подходят ни для чего другого.
Дополнительные разделы математики
Хотя 90% ваших вопросов попадут в категории «Алгебра», «Паспорт для продвинутой математики» или «Решение проблем и анализ данных», оставшиеся 10% будут просто классифицированы как «Дополнительные темы».Эти темы включают в себя геометрию, тригонометрию и задачи с комплексными числами.
Официальные темы
- Проблемы с объемным словом
- Задачи со словами в прямоугольном треугольнике
- Соответствие и сходство
- Геометрия прямоугольного треугольника
- Углы, длина дуги и триггерные функции
- Круговые теоремы
- Уравнения окружности
- Комплексные числа
Сводка задач
- Определите объем формы.
- Примените свойства треугольников, чтобы определить длину стороны или угол.
- Примените свойства окружностей для измерения длины и площади дуги.
- Решите проблемы с синусом, косинусом и тангенсом.
Примеры вопросов
Задача прямоугольного треугольника с тригонометрическими функциями:
Сравнение и сходство:
Углы и параллельные прямые:
Чтобы по-настоящему подготовиться к математическому разделу SAT, вы должны обязательно изучить все вышеупомянутые темы.Некоторые проблемы, кроме того, объединяют темы и требуют от вас применения нескольких навыков и концепций в процессе работы над решением. Многоступенчатые задачи распространены в математическом разделе. Давайте подробнее рассмотрим многоступенчатые задачи, а также другие основные функции , о которых вам нужно знать, когда вы готовитесь к SAT Math.
Возьмите закуски и выключите мобильный телефон — пришло время для основных функций!
Каковы основные особенности SAT Math?
Помимо понимания содержания и формата раздела SAT Math, есть некоторые ключевые особенности , о которых вы должны знать. Во время изучения следите за этими функциями. Ознакомившись с ними, вы даже сможете эффективно использовать практические материалы для старого SAT, чтобы подготовиться к текущему SAT.
Многоступенчатые задачи
Вы можете заметить, что некоторые из вышеперечисленных типов проблем заявляют, что для их решения требуется несколько шагов. Хотя формулировки математических вопросов должны быть простыми, требуемые размышления и вычисления будут относительно сложными. Чтобы подготовиться, вам особенно нужно сосредоточиться на управлении временем и работе быстро и эффективно.
Чтобы решить проблему со словом, вам, возможно, придется объединить навыки из более чем одной области содержания или использовать несколько шагов, чтобы найти ответ. Проблемы с Word могут представлять собой длинный сценарий, и вам нужно будет выяснить, какие данные использовать и какие концепции применить, чтобы получить ответ. Кстати о проблемах со словами …
Акцент на приложениях «реального мира»
Согласно College Board, основная цель редизайна SAT заключалась в том, чтобы сделать тест более тесно связанным с обучением в классе и навыками реального мира. В результате в математическом разделе не будет слишком много абстрактных вопросов для рассуждений.
Вместо этого, проблемы со словом будут основаны на реальных ситуациях. Некоторые могут попросить вас подсчитать количество бензина, оставшегося в бензобаке автомобиля, или пересчет денег из валюты одной страны в валюту другой. Большинство задач со словами представляют собой сценарии, с которыми вы можете столкнуться в своей жизни.
Будет несколько вопросов, которые проверят ваше понимание синусов.А также косинусы и касательные.
Несколько вопросов о геометрии и тригонометрии
Около 10% вопросов будут касаться геометрии и / или тригонометрии. Поскольку не все изучали тригонометрию в школе к моменту сдачи SAT, для этих вопросов может потребоваться отдельная подготовка к SAT.
Вам следует познакомиться с соответствующими концепциями и формулами, но сосредоточить большую часть своей энергии на подготовке к алгебре, функциям, неравенствам, графикам и задачам со словами.
Раздел без калькулятора и раздел калькулятора
В течение 25 минут вы не сможете достать калькулятор, чтобы ответить ни на один из математических вопросов. Не о чем беспокоиться! Для задач в 25-минутном разделе калькулятор не потребуется; на самом деле, использование одного для решения этих проблем, вероятно, просто замедлит вас.
Свободное владение калькулятором , то есть знание того, как и когда эффективно использовать калькулятор, является важным навыком при выполнении SAT-математики.Совет колледжа говорит: «Калькуляторы — важные инструменты, и … вам нужно знать, как — и когда — использовать их … Калькулятор, как и любой другой инструмент, настолько умен, насколько умен человек, использующий его. Математический тест включает в себя несколько вопросов, по которым лучше не использовать калькулятор, даже если вам разрешено «.
Таким образом, вам определенно не понадобится один в более коротком разделе «без калькулятора», а вам, , может даже не понадобиться для решения многих задач в более длинном разделе «калькулятор». Ответы на множество практических вопросов помогут вам лучше понять, когда калькулятор будет полезен, а когда он просто замедлит вас.
Проблема расширенного мышления
Некоторые из ваших вопросов будут частью проблемы расширенного мышления. Как правило, эта проблема расширенного мышления будет составлять часть вопросов сетки ближе к концу вашего 55-минутного раздела.
По сути, вы получите сценарий проблемы с графиком, таблицей или текстом, а затем вам нужно будет ответить на несколько вопросов по этому поводу. Ниже приводится один из примеров вопроса о расширенном мышлении, основанного на проблеме.Обратите внимание на склонность к применению «реального мира»!
Сетка математических вопросов
Говоря о сетках, у вас будет тринадцать таких ответов учеников, на которые вы ответите в специальной части пузырькового листа внизу. Хотя вы можете написать свой ответ в отведенных для этого полях, вам придется заполнить соответствующие кружки для получения кредита. Есть пузыри для цифр от 0 до 9, а также для десятичной точки (точка) и дробной черты (косая черта).Чтобы попрактиковаться в построении сетки в своих ответах, вы можете потренироваться на листе ответов на практический тест College Board SAT.
Если вы знакомы с ключевыми функциями и направлениями SAT Math, вы можете приступить к работе с и не тратить время на выяснение логистики. Итак, готовитесь ли вы с помощью PrepScholar, вопросов онлайн-практики, официальных тестов College Board или комбинации всего этого, как вам следует подойти к подготовке к SAT Math?
Раскройте потенциал подготовки.
Как следует изучать SAT Math
Многие концепции SAT Math вы изучите на уроках математики в школе. Однако это не означает, что работа в классе подготовит вас достаточно для успешной сдачи SAT. Вопросы SAT Math проверяют вышеупомянутые концепции уникальным, специфичным для SAT способом . Чтобы подготовиться и научиться быстро управлять своим временем, вам нужно попрактиковаться и познакомиться с формулировками с помощью высококачественных практических вопросов.
Официальные практические тесты также помогут вам выявить и диагностировать свои сильные и слабые стороны . Например, если вас постоянно ставят в тупик функциональные вопросы, вы будете знать, что нужно сосредоточить на них свою энергию и учиться. Даже если вы еще не прошли углубленный курс алгебры или тригонометрии в школе, вы все равно можете подготовиться к этим вопросам, изучая концепции и вопросы SAT.
Если вы сильны в математике и хотите набрать больше баллов, вам нужно подойти к математическому разделу со стратегической точки зрения.Соучредитель PrepScholar и отличник SAT Аллен Ченг делится методами, которые он использовал, и о том, как они могут помочь вам набрать 800 или около того на вашем SAT математике.
Что дальше?
У вас низкие оценки по математике и вы надеетесь побить 600? Вот шаги, которые необходимо предпринять, чтобы набрать 600 или более баллов по математике SAT.
Ищете рекомендации по книгам по математическому разделу? Вот наши предложения по лучшим учебникам для подготовки к SAT Math, а также несколько советов о том, как их использовать наиболее эффективно.
Хотите убедиться, что вы хорошо разбираетесь в математике, прежде чем углубляться в SAT Math? Ознакомьтесь с нашими дополнительными статьями о решении неравенств, сложении и вычитании дробей, умножении, точных квадратах и свойстве распределения.
Хотите улучшить свой результат SAT на 160 баллов?
Посетите наши лучшие в своем классе онлайн-классы подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой SAT на 160 или более баллов.
Наши классы полностью онлайн, и их ведут эксперты SAT. Если вам понравилась эта статья, вам понравятся наши классы. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно.