Формулы егэ по математике – школьные формулы по алгебре и геометрии - Управленческое образование

Формулы тригонометрии. Основные тригонометрические формулы для ЕГЭ

Для того чтобы сдать ЕГЭ по математике, вам понадобится около 20 формул тригонометрии. Это не много. Но их надо знать наизусть!

Вот таблица, в которой собраны основные тригонометрические формулы. Здесь все самое необходимое. Их легко выучить и применять.

Ты нашел то, что искал? Поделись с друзьями!

Кроме того, надо знать определения синуса, косинуса и тангенса, а также значения этих функций для основных углов.

Это необходимый минимум. Тем, кто рассчитывает на высший балл, понадобится еще несколько формул тригонометрии.

Как же выучить тригонометрические формулы?

1. Учите формулы сразу. Не рассказывайте себе сказки о том, что в последнюю ночь перед ЕГЭ все выучите. Каждый день – один блок, то есть три-четыре формулы из нашей таблицы.

2. Тренируйтесь. Выучить иностранный язык проще всего тому, кто вынужден постоянно на нем говорить. Так и здесь. Для тренировки можно из классического задачника Сканави выбрать 20-50 заданий на преобразование тригонометрических выражений и доказательство тождеств.

3. Универсальный способ: ежедневно, садясь за уроки, берите чистый листок и выписывайте наизусть все тригонометрические формулы, какие помните. Когда всё готово — сверяете. И к экзамену вы будете помнить всё.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Материал для подготовки к ЕГЭ (ГИА) по алгебре (11 класс) по теме: Формулы к ЕГЭ по математике

Формулы сокращенного умножения

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Куб суммы:

Куб разности:

Сумма кубов:

Разность кубов:

Основные свойства степеней

a1 = а, a0 = 1, a-n = 1/an (a ≠ 0), am/n = m

1° aman = am+n;

2° am/an = am-n;

3° (ab)n = anbn;

4° (am)n = amn;

5° (a/b)n = an/bn.

Основные свойства корней

1° ;

2° ( b);

3° = ( k>);

4° k ( k>);

5° k = () k ( если k)

Формулы и свойства логарифмов

loga b = x, ax = b.

Логарифм числа b по основанию a – loga b (a > 0, a ≠ 1, b > 0)

Десятичный логарифм – lg b (Логарифм по основанию 10, а = 10).

Натуральный логарифм – ln b (Логарифм по основанию e, а = e).

1° alogab = b – основное логарифмическое тождество;

2° loga 1 = 0;

3° loga a = 1;

4° loga (xy) = loga x + loga y;

5° loga () = logax — logay;

6° loga xp = p logax;

7° log(ac )b = logab;

8° logax = (logbx)/(logba) – формула перехода к новому основанию

9° logab = 1/logba;

Таблица производных

(C)I = 0

(x)I = 1

(xn)I = nxn-1

()I =

(ex)I = ex

(ax)I = ax ln a

(ln x)I =

(sin x) I = cos x

(cos x) I = — sin x

(tg x) I = 1/cos2x

(ctg x) I = — 1/sin2x

(cu)I=cuI

(u ± v)I = uI ± vI

(uv)I = uI v+ u vI

( )I = (uI v — u vI)/ v2

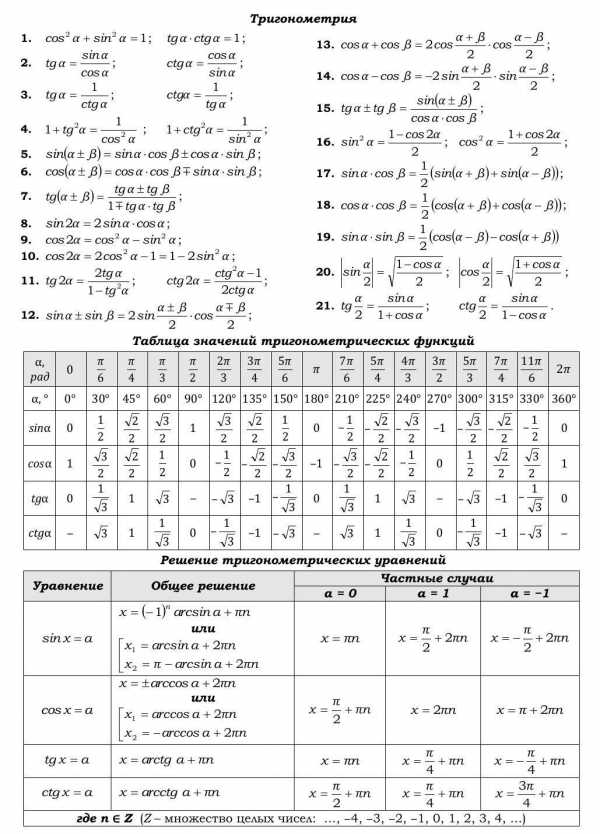
Тригонометрия

Значения тригонометрических функций некоторых углов

α	0
sin α	0		1	0	-1
cos α	1		0	-1	0
tg α	0	1	—	0	—
ctg α	—	1	0	—	0

sin α=    (отношение противолежащего катета к гипотенузе).
cos α=   (отношение прилежащего катета к гипотенузе).
tg α=   (отношение противолежащего катета к прилежащему).
ctg α= (отношение прилежащего катета к противолежащему).

1. Перед приведенной функцией ставится тот знак, который имеет исходная функция, если 0

2. Функция меняется на кофункцию, если n нечетно, и не меняется, если n четно. Кофункциями для функций синуса, косинуса, тангенса и котангенса соответсвенно являются косинус, синус, котангенс и тангенс.

cos(-α) = cos α; sin2α=2 sinα cosα

sin(-α) = — sin α; cos2α=cos2α – sin2α
tg(-α) = — tg α;
ctg(-α) = — ctg α.

Решение простейших тригонометрических уравнений

sin t = a

если a>1, то уравнение не имеет решений;

если 0k arcsin a + k, kZ;

если -1k+1 arcsin(-a) + k, kZ;

если a=1, то t = +2n , nZ;

если a=-1, то t = — + 2n , nZ;

если a=0, то t = n , nZ;

cos t = a

если a>1, то уравнение не имеет решений;

если 0 arccos a + 2n, nZ;

если -1 (-arccos(-a)) + 2n, nZ;

если a=1, то t = 2n , nZ;

если a=-1, то t =  + 2n , nZ;

если a=0, то t = +n , nZ;

tg t = a

t = arctg a + n, nZ;

ctg t = a

tg t = ; t = arctg + n, nZ;

Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

с2 = a2 + b2

Теорема. В прямоугольном треугольнике напротив угла в 30° лежит катет равный половине гипотенузы.

Если угол α=30°, то a= c

sin ے1 = cos ے2

cos ے1=sin ے2

sin ے3=sin ے2

cos ے3= cos ے2

Теорема. Угол вписанный в окружность равен половине соответствующего центрального угла

ےBAC = ےBOC

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

a2= b2 + с2 – 2bc cosα

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема. Сумма углов выпуклого n-угольника равна 180° · ( n– 2 )

Формулы для радиусов вписанной и описанной окружностей треугольника.

R = r = ,

где a, b, c – стороны треугольника, а S – его площадь

АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ

Арифметическая прогрессия — это последовательность чисел, каждое из которых получается из предыдущего путем прибавления к нему одного и того же числа d, называемого разностью этой арифметической прогрессии.

Формула n-го члена:

Формулы суммы n первых членов:

ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ

Геометрическая прогрессия — это последовательность чисел, каждое из которых равно предыдущему, умноженному на некоторое постоянное для данной прогрессии число q, называемое знаменателем этой геометрической прогрессии.

Формула n-го члена:

Формулы суммы n первых членов:

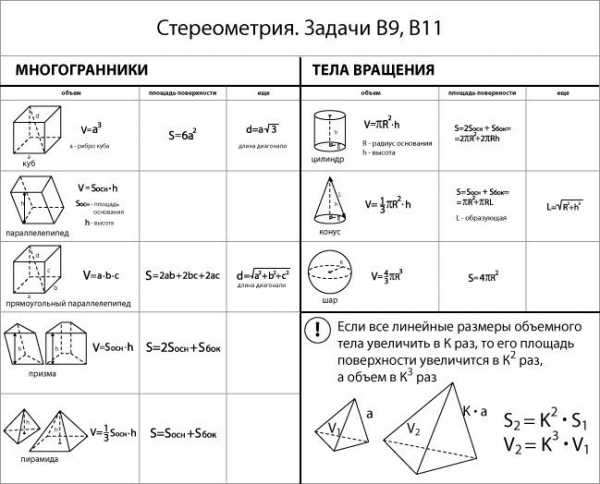
Площадь треугольника:

1) S = a·h

2) S = b ·c ·sinA

3) Формула Герона: S = , p =

Площадь прямоугольника:

S = a·b

P=2(a+b)

Площадь параллелограмма:

S = AD·h
S =AD·AB·sinA

Площадь ромба:

S = ·AC ·BD

Площадь трапеции:

S =

Средняя линия трапеции:

MN =

Площадь круга:

S = 𝝅R2

Длина окружности:

L=2𝝅R

Шар

Sсферы=4𝝅R2

V= 𝝅R3

Призма

V=Sосн.·h

Sполн.=2Sосн.+Sбок.

Sбок.=Pосн.·h (для прямой призмы)

Пирамида

V= Sосн.·h

Sполн.=Sосн.+Sбок.

Sбок.=Pосн.·l (для прав. пирамиды)

Цилиндр

V=Sосн.·h= 𝝅R2h

Sполн.=2Sосн.+Sбок.= =2𝝅R2+2𝝅Rh

Sбок.=Lокр.·h= 2𝝅Rh

Конус

V=Sосн.·h= 𝝅R2h

Sполн.=Sосн.+Sбок.= =𝝅R2+𝝅Rl

Sбок.=Lокр.·l= 𝝅Rl

Прямоугольный параллелепипед

V= abc

Sполн.=2(ab+bc+ac)

d2 = a2 + b2 +c2

Куб

V= a3

Sполн.=6а2

nsportal.ru

Справочные материалы. ЕГЭ по математике. Определения, формулы, таблицы

ГЛАВНАЯ
ПОДГОТОВКА К ШКОЛЕ (5 — 6 лет)
Тест «ГОТОВНОСТЬ РЕБЕНКА К ШКОЛЕ»
ПРЕДМЕТЫ НАЧАЛЬНОЙ ШКОЛЫ (1-4 классы)
ПОВЫШЕНИЕ ТЕКУЩЕЙ УСПЕВАЕМОСТИ (5-11 классы) по математике, физике и др. предметам. Подготовка к ОГЭ и ЕГЭ

Справочные материалы. ЕГЭ по математике. Определения, формулы, таблицы
ЕГЭ: информация, полезные ссылки
СТАТЬИ
- Как правильно держать ручку при письме
- Легкий способ научить ребенка читать
- Как научить ребенка считать
- Готовность к школе. Советы психолога
- Нестрашная математика
- Надо ли школьнику заниматься на каникулах?
РЕПЕТИТОРАМ
КОНТАКТЫ

ГЛАВНАЯ
ПОДГОТОВКА К ШКОЛЕ (5 — 6 лет)
Тест «ГОТОВНОСТЬ РЕБЕНКА К ШКОЛЕ»
ПРЕДМЕТЫ НАЧАЛЬНОЙ ШКОЛЫ (1-4 классы)
ПОВЫШЕНИЕ ТЕКУЩЕЙ УСПЕВАЕМОСТИ (5-11 классы) по математике, физике и др. предметам. Подготовка к ОГЭ и ЕГЭ

Справочные материалы. ЕГЭ по математике. Определения, формулы, таблицы
ЕГЭ: информация, полезные ссылки
СТАТЬИ
- Как правильно держать ручку при письме
- Легкий способ научить ребенка читать
- Как научить ребенка считать
- Готовность к школе. Советы психолога
- Нестрашная математика
- Надо ли школьнику заниматься на каникулах?
РЕПЕТИТОРАМ
КОНТАКТЫ