| 2447 | В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай равна 0,4. Вероятность того, что чай закончится в обоих автоматах равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах Решение | В торговом центре два одинаковых автомата продают чай ! Математика 50 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 9 Задание 4 # Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 4 Задание 4 # Задача — Аналог 1503 1459 | |
| 2446 | Брюки дороже рубашки на 30% и дешевле пиджака на 22%. На сколько процентов рубашка дешевле пиджака Решение | Брюки дороже рубашки на 30% и дешевле пиджака на 22% ! Математика 50 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 9 Задание 11 # Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 4 Задание 11 | |
| 2445 | Решите неравенство 4^(x-3)-71*2^(x-6)+7 <= 0 Решение График | Решите неравенство 4^(x-3) -71 *2^(x-6) +7 <= 0 ! Математика 50 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 9 Задание 15 # Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 4 Задание 15 | |
| 2439 | Андрей отправляет СМС другу. Связь не очень устойчивая, по этому каждая попытка отправить СМС имеет вероятность успеха 0,8. Найдите вероятность того, что СМС будет отправлена с третьей попытки Связь не очень устойчивая, по этому каждая попытка отправить СМС имеет вероятность успеха 0,8. Найдите вероятность того, что СМС будет отправлена с третьей попыткиРешение | Андрей отправляет СМС другу. Связь не очень устойчивая ! Математика 50 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 8 Задание 4 # Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 3 Задание 4 | |
| 2438 | Шар, объём которого равен 14pi, вписан в куб. Найдите объём куба Решение | Шар, объём которого равен 14 пи, вписан в куб ! Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 3 Задание 8 | |
| 2437 | Вычислите значение выражения 3^(log_{3}(7))+49 ^(log_{7}(sqrt(13))) Решение График | Вычислите значение выражения 3 в степени логарифм по основанию 3 из 7 + 49 ! Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 3 Задание 9 | |
| 2436 | Из пункта A круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92 км/ч, скорость второго — 77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на один круг? Скорость первого равна 92 км/ч, скорость второго — 77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на один круг?Решение | Из пункта A круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста ! Математика 50 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 8 Задание 11 # Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 3 Задание 11 | |
| 2435 | Найдите наибольшее значение функции y=6sin(x)-3sqrt(3)x+0.5sqrt(3)pi+6 на отрезке [0; pi/2]. Решение График | Найдите наибольшее значение функции y= 6 sin x — 3 корня из 3 x + 0.5 корня из 3 * пи +6 ! Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 3 Задание 12 | |
| 2434 | Решите неравенство log_{root(8)(16)}(log_{1/4}(x+2)) >= 2. Решение График | Решите неравенство log по основанию корень 8 степени из 16 * log 1/4 (x+2)) > = 2 ! Математика 50 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 7 Задание 15 # Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 2 Задание 15 | |
| 2433 | Одиннадцать одинаковых рубашек дешевле куртки на 1%. На сколько процентов четырнадцать таких же рубашек дороже куртки? Решение | 11 одинаковых рубашек дешевле куртки на 1% ! Математика 50 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 7 Задание 11 # Математика 37 вариантов ЕГЭ 2021 профильный уровень Ященко Вариант 2 Задание 11 # Задача-аналог 2431 | |
Московский комсомолец: «Иван Ященко опроверг усложнение ЕГЭ по математике 2022»
Пока выпускники-2022 гадают, не нарушит ли сроки сдачи ЕГЭ пандемия, многих из них встревожило сообщение, прошедшее по многим каналам об усложнении экзамена по математике.
Дело в том, что произошло недопонимание: профильное ведомство дало информацию об уже зафиксированной в ЕГЭ норме, усложненной ранее. По просьбе «МК» ситуацию прояснил руководитель группы разработчиков ЕГЭ по математике Иван Ященко.
– Никаких изменений в ЕГЭ в декабре, январе, ноябре не бывает. Все изменения в ЕГЭ объявляются к 1 сентября. В августе на сайте ФИПИ были опубликованы все материалы, они обсуждались на съезде учителей, на августовских семинарах… Почему сейчас поднялась волна сообщений о каких-то изменениях, не понимаю.
Более того, та модель ЕГЭ, которая будет сейчас – это та модель, которая была представлена 2 года назад и прошла широкую апробацию, обсуждалась по всей стране. Сейчас окончательно завершено разделение ЕГЭ по математике на базовый и профильный уровни. Несколько лет были переходными, сейчас экзамен окончательно оформился.
Профильный уровень математики теперь соответствует всем требованиям, которые есть в технических, экономических и других вузах на специальностях, где требуется математика. Это повышенный или высокий уровень подготовки, который с помощью профильного ЕГЭ выпускник может продемонстрировать.
Базовая математика позволяет ребятам показать знания, которые нужны выпускнику, поступающему на гуманитарные или аналогичные специальности. Все задания полностью соответствуют школьной программе. Надо отметить, что теперь в базовом ЕГЭ два задания по теории вероятности, а раньше было одно. Этот раздел был включен в стандарт еще в 2004 году. То есть, вот такой долгий переходный период, сразу такие вещи не происходят. Вероятность и статистика теперь нужны всем, практически, в любой профессии требуется оценка и анализ.
Так что информация об изменениях в ЕГЭ по математике – августовская. Три задания ушли, два добавились. Два года назад об этом было объявлено, год уже действует ЕГЭ в таком виде. В августе на ФИПИ были размещены обновленные задания по математике. Все учителя, все школьники уже давно с этими заданиями ознакомлены. Результаты, уверен, будут сопоставимы с прошлогодними…
В августе на ФИПИ были размещены обновленные задания по математике. Все учителя, все школьники уже давно с этими заданиями ознакомлены. Результаты, уверен, будут сопоставимы с прошлогодними…
По сообщению Рособрнадзора, в базовую математику, которую сдают те выпускники, что не пойдут в технические вузы, добавлена одна «практико-ориентированная текстовая задача». Есть изменения и в разделе геометрии, там «усилен практико-ориентированный акцент». Эксперты поясняют, что речь о стереометрии – разделе математики, изучающей положение точек, линий и фигур в системе координат.
«В экзаменационную работу добавлены задание № 5, проверяющее умение выполнять действия с геометрическими фигурами, — сообщает ведомство. И упоминает еще и задание № 20, «проверяющее умение строить и исследовать простейшие математические модели». С демоверсиями заданий по-прежнему можно ознакомиться на сайте ФИПИ.
В ведомстве напоминают, что сроки сдачи не меняются.
Уровень сложности заданий комментирует доцент кафедры высшей математики, кандидат наук Ярослав Талашко.
– В разделе базовой математики ряд заданий в начале раздела простые, – говорит Ярослав. – Конкретно, по геометрии, задания на нахождение объема фигур, треугольник, вписанный в прямоугольник, нахождение длины окружности… Со всем этим выпускник школы вполне справится. Есть задания, где требуется нестандартность мышления. Задача о садоводах с круглым прудом посередине или на объем жидкости, налитой в призму, к примеру.
О профильной математике что сказать? Это серьезный уровень, который требует серьезной подготовки. Привлекло внимание то обстоятельство, что относительно немного тригонометрии, зато много логарифмических задач, заданий на нелинейные функции. Много привязано к практике – бизнес, тайм-менеджмент. Что ж, это влияние времени.
Более 86 тысяч человек зарегистрировались на сдачу ЕГЭ в Москве
https://sn.ria.ru/20220202/ege-1770616467.html
Более 86 тысяч человек зарегистрировались на сдачу ЕГЭ в Москве
Более 86 тысяч человек зарегистрировались на сдачу ЕГЭ в Москве — РИА Новости, 02. 02.2022
02.2022
Более 86 тысяч человек зарегистрировались на сдачу ЕГЭ в Москве
Более 86 тысяч человек зарегистрировались на сдачу ЕГЭ в Москве, основной период начнется 26 мая с экзаменов по географии, литературе и химии, сообщается на… РИА Новости, 02.02.2022
2022-02-02T09:53
2022-02-02T09:53
2022-02-02T09:53
общество
москва
единый государственный экзамен (егэ)
социальный навигатор
сн_образование
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e5/06/03/1735384545_0:159:3079:1890_1920x0_80_0_0_50dd429cec6bbd6b6d197b214d69de97.jpg
МОСКВА, 2 фев — РИА Новости. Более 86 тысяч человек зарегистрировались на сдачу ЕГЭ в Москве, основной период начнется 26 мая с экзаменов по географии, литературе и химии, сообщается на официальном сайте мэра столицы.Отмечается, что в Москве завершилась регистрация на участие в государственной итоговой аттестации по образовательным программам среднего общего образования (ЕГЭ, ГВЭ), подать заявление можно было в электронном виде на портале mos. ru до 1 февраля включительно.Отмечается, что основной период ЕГЭ-2022 начнется с экзаменов по географии, литературе и химии. Экзамен по русскому языку пройдет 30 и 31 мая, по информатике и информационно-коммуникационным технологиям — 20 и 21 июня, устная часть ЕГЭ по иностранным языкам запланирована на 16 и 17 июня. Экзамен по профильной и базовой математике состоится 2 и 3 июня соответственно. 6 июня пройдут экзамены по истории и физике, 9 июня — по обществознанию, 14 июня — по биологии, а также письменная часть ЕГЭ по иностранным языкам. С 23 июня по 2 июля в расписании предусмотрены резервные дни для сдачи экзаменов по всем предметам.В дополнительный период в сентябре пройдут экзамены только по обязательным предметам (русскому языку и базовой математике) для тех выпускников, которые не получили аттестат.
ru до 1 февраля включительно.Отмечается, что основной период ЕГЭ-2022 начнется с экзаменов по географии, литературе и химии. Экзамен по русскому языку пройдет 30 и 31 мая, по информатике и информационно-коммуникационным технологиям — 20 и 21 июня, устная часть ЕГЭ по иностранным языкам запланирована на 16 и 17 июня. Экзамен по профильной и базовой математике состоится 2 и 3 июня соответственно. 6 июня пройдут экзамены по истории и физике, 9 июня — по обществознанию, 14 июня — по биологии, а также письменная часть ЕГЭ по иностранным языкам. С 23 июня по 2 июля в расписании предусмотрены резервные дни для сдачи экзаменов по всем предметам.В дополнительный период в сентябре пройдут экзамены только по обязательным предметам (русскому языку и базовой математике) для тех выпускников, которые не получили аттестат.
https://na.ria.ru/20220201/priem-2022-1764942919.html
москва
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og. xn--p1ai/awards/
xn--p1ai/awards/
2022
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Новости
ru-RU
https://sn.ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/07e5/06/03/1735384545_66:0:2795:2047_1920x0_80_0_0_544ebd8a60c2c2f17d3a1323f568d72d.jpgРИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
общество, москва, единый государственный экзамен (егэ), социальный навигатор, сн_образование
МОСКВА, 2 фев — РИА Новости. Более 86 тысяч человек зарегистрировались на сдачу ЕГЭ в Москве, основной период начнется 26 мая с экзаменов по географии, литературе и химии, сообщается на официальном сайте мэра столицы.
Более 86 тысяч человек зарегистрировались на сдачу ЕГЭ в Москве, основной период начнется 26 мая с экзаменов по географии, литературе и химии, сообщается на официальном сайте мэра столицы.
Отмечается, что в Москве завершилась регистрация на участие в государственной итоговой аттестации по образовательным программам среднего общего образования (ЕГЭ, ГВЭ), подать заявление можно было в электронном виде на портале mos.ru до 1 февраля включительно.
«В этом году выпускные экзамены проведут в три этапа: досрочный период пройдет с 21 марта по 18 апреля, основной — с 26 мая по 2 июля и дополнительный — с 5 по 20 сентября. Заявления на участие в ЕГЭ в 2022 году подали более 86 тысяч человек, из них 69 тысяч — выпускники текущего года», — рассказал первый заместитель директора Московского центра качества образования Андрей Постульгин.
Отмечается, что основной период ЕГЭ-2022 начнется с экзаменов по географии, литературе и химии. Экзамен по русскому языку пройдет 30 и 31 мая, по информатике и информационно-коммуникационным технологиям — 20 и 21 июня, устная часть ЕГЭ по иностранным языкам запланирована на 16 и 17 июня. Экзамен по профильной и базовой математике состоится 2 и 3 июня соответственно. 6 июня пройдут экзамены по истории и физике, 9 июня — по обществознанию, 14 июня — по биологии, а также письменная часть ЕГЭ по иностранным языкам. С 23 июня по 2 июля в расписании предусмотрены резервные дни для сдачи экзаменов по всем предметам.
Экзамен по профильной и базовой математике состоится 2 и 3 июня соответственно. 6 июня пройдут экзамены по истории и физике, 9 июня — по обществознанию, 14 июня — по биологии, а также письменная часть ЕГЭ по иностранным языкам. С 23 июня по 2 июля в расписании предусмотрены резервные дни для сдачи экзаменов по всем предметам.
В дополнительный период в сентябре пройдут экзамены только по обязательным предметам (русскому языку и базовой математике) для тех выпускников, которые не получили аттестат.
Три отняли, два добавили. Какие изменения в ЕГЭ по математике ждут выпускников-2022
Тег audio не поддерживается вашим браузером.В Рособрнадзоре объявили об обновлении контрольно-измерительных материалов Единого госэкзамена и разъяснили нюансы одного из обязательных предметов – математики.
Напомним: с этого года экзаменационные материалы ЕГЭ по всем предметам теперь полностью соответствуют ФГОС среднего общего образования.
«Обновленные контрольные измерительные материалы (КИМ) ЕГЭ в большей степени ориентированы не на проверку предметных знаний, а на умение их использовать для решения различных познавательных, практических и коммуникативных задач», — сообщили в ведомстве.
Пояснения в измененном содержании КИМов в Рособрнадзоре начали с математики, которая окончательно разделена на базовый и профильный уровни. Разобраться в деталях ulpravda.ru помог директор Центра мониторинга и статистики образования, ресурсов и информационных систем Института развития образования Евгений Тихомиров.
Математика базового уровня
Удалено задание 2, проверяющее умение выполнять вычисления и преобразования (это требование внесено в позицию задачи 7 в новой нумерации).
Добавлены:
— задание 5, проверяющее умение выполнять действия с геометрическими фигурами;
— задание 20, проверяющее умение строить и исследовать простейшие математические модели.
Количество заданий увеличилось с 20 до 21, максимальный балл за выполнение всей работы стал равным 21.
Математика профильного уровня
Удалены:
— задания 1 и 2, проверяющие умение использовать приобретённые знания и умения в практической и повседневной жизни;
— задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.
Добавлены:
— задание 9, проверяющее умение выполнять действия с функциями;
— задание 10, проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
Откорректирована система оценивания выполненных заданий:
— максимальный балл за выполнение задания повышенного уровня 13 (он направлен на умение выполнять действия с геометрическими фигурами, координатами и векторами) отныне равен 3;
— максимальный балл за выполнение задания повышенного уровня 15 (умение использовать приобретённые знания в практической деятельности и повседневной жизни), равен 2.
Всего выпускникам предстоит выполнить 18 (ранее было 19). При этом максимальный балл за решение всех заданий равен 31.
«При решении задач придется обосновать результат, сделать выводы. Появятся задания из «жизни» — о кредитах, покупках и т.д. При этом все задания полностью основаны на школьной программе», — пояснил Евгений Тихомиров.
Впоследствии Рособрнадзор огласит изменения в ЕГЭ по всем предметам, утвержденные еще в прошлом году. Главную канву нововведений в ЕГЭ по биологии, истории, географии, русскому языку, литературе и обществознанию мы приводили ранее.
С демоверсиями КИМ ЕГЭ-2022 каждый выпускник может ознакомиться на сайте ФИПИ: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory
О сроках проведения ЕГЭ-2022 и минимальном пороге – читайте здесь.
Изменений в ОГЭ в этом году нет.
Рособрнадзор внёс изменения в ЕГЭ по математике в 2022 году
В ЕГЭ по математике в 2022 году внесены изменения: в профильном экзамене уберут часть слишком простых заданий и добавят более сложные. Об этом пишет РБК со ссылкой на Рособрнадзор.
Об этом пишет РБК со ссылкой на Рособрнадзор.
В экзамене по математике базового уровня – его сдают те, кому предмет для поступления в вуз не нужен, – появилась ещё одна практико-ориентированная текстовая задача и «усилен практико-ориентированный акцент в заданиях по геометрии». Изменён порядок заданий и максимальный первичный балл.
В работу добавили задание № 5, проверяющее умение выпускника выполнять действия с геометрическими фигурами, и задание № 20, которое проверяет умение строить и исследовать простейшие математические модели.
Из профильного экзамена по математике убрали ряд заданий базового уровня сложности, с которыми все участники легко справлялись. Вместо них появились более сложные задачи, «позволяющие лучше дифференцировать выпускников по уровню подготовки».
«Участникам ЕГЭ в 2022 году больше не встретятся практическая задача на делимость, практическая задача на график реальной зависимости и задание базового уровня по геометрии. При этом в КИМ добавлены два новых задания (алгебраическое задание с использованием графика функции и задание по теории вероятности повышенного уровня сложности). Также были скорректированы система оценивания и критерии проверки двух заданий с развёрнутым ответом», – сообщили в Рособрнадзоре.
При этом в КИМ добавлены два новых задания (алгебраическое задание с использованием графика функции и задание по теории вероятности повышенного уровня сложности). Также были скорректированы система оценивания и критерии проверки двух заданий с развёрнутым ответом», – сообщили в Рособрнадзоре.
Демоверсия ЕГЭ по математике есть на сайте Федерального института педагогических измерений.
Напомним, из-за пандемии коронавируса и частой отмены занятий в 2021 году обязательный ЕГЭ по базовой математике отменили. Для получения аттестата было достаточно сдать ЕГЭ по русскому языку. Выпускники, которые не планировали поступать в вузы, могли сдать государственный выпускной экзамен (ГВЭ) по русскому языку и математике.
В 2022 году базовый экзамен вернётся. В Рособрнадзоре уже предупреждали, что планов упрощать его из-за пандемии нет.
Математическое моделирование вспышек вариантов SARS-CoV-2 показывает вероятность их исчезновения сначала рассмотрим динамику элементарной инфекции между двумя людьми P1 и P2, из которых P1 инфицирован, а P2 восприимчив.
 Рассмотрим бесконечно малый интервал времени \([t,t+dt]\), где P1 и P2 находятся в пределах зоны заражения.Моделирование состояния заражения P2 как цепи Маркова с непрерывным временем (CTMC) с двумя состояниями дает вероятность того, что P1 заразит P2 в течение \([t,t+dt]\), равной \(b \ dt\), где b – константа характеристики болезни.
Рассмотрим бесконечно малый интервал времени \([t,t+dt]\), где P1 и P2 находятся в пределах зоны заражения.Моделирование состояния заражения P2 как цепи Маркова с непрерывным временем (CTMC) с двумя состояниями дает вероятность того, что P1 заразит P2 в течение \([t,t+dt]\), равной \(b \ dt\), где b – константа характеристики болезни. Рассмотрим восприимчивого индивидуума P, взаимодействующего с популяцией, состоящей из x инфицированных, численностью популяции N . Если предположить, что P в среднем находит L других людей в пределах своего диапазона заражения, то средняя вероятность заражения P в течение \([t,t+dt]\) равна \(b L \frac{x {N} дт\).
Рассмотрим следующие S восприимчивых особей, каждый из которых взаимодействует с популяцией, состоящей из x инфицированных из популяции размером N . Тогда вероятность заражения 1 из восприимчивых лиц в \([t,t+dt]\) приблизительно равна
$$\begin{aligned} b L \frac{S x}{N} dt = \beta \frac{S x}{N} dt. \end{выровнено}$$
\end{выровнено}$$
(1)
Это приводит к следующему дифференциальному уравнению, определяющему эволюцию ожиданий:
$$\begin{aligned} \frac{d}{dt} E(x) = E\left( \beta \frac{S x}{N }\right) \приблизительно \beta \frac{E(S) E(x)}{N} \end{aligned}$$
(2)
, включающее уравнение скорости заражения модели SIR.Когда незащищенное состояние вставляется между восприимчивым и зараженным состояниями, (2) дает скорость передачи между уязвимым и незащищенным состояниями.
Если рассматривать вместо ожиданий распределение вероятностей по фактическому числу зараженных I , (1) приводит к
$$\begin{aligned} P(x(t+dt)=k | x(t)= k-1) = \beta \frac{S (k-1)}{N} dt \end{aligned}$$
и с законом полной вероятности Байеса
$$\begin{align} P(x (t+dt)=k)= & {} P(x(t+dt)=k | x(t)=k-1) P(x(t)=k-1) + P(x(t+ dt)=k | x(t)=k) P(x(t)=k) \\= & {} \beta \frac{S (k-1)}{N} dt P(x(t)= k-1) + (1-\beta \frac{S k}{N} dt) P(x(t)=k) \end{aligned}$$
, что дает
$$\begin{align} \ frac{P(x(t+dt)=k)-P(x(t)=k)}{dt} = \beta \frac{S (k-1)}{N} P(x(t)= (k-1)) — \beta \frac{S k}{N} P(x(t)=k). \end{aligned}$$
\end{aligned}$$
Приводя к дифференциальному уравнению
$$\begin{aligned} \frac{d}{dt}P(x(t)=k) = \beta \frac{S (k- 1)}{N} P(x(t)=k-1) — \beta \frac{S k}{N} P(x(t)=k) \end{aligned}$$
Для раннего развитие вспышки \(S\ок N\). Это дает динамику заражения
$$\begin{aligned} \frac{d}{dt}P(x(t)=k) = \beta (k-1) P(x(t)=k-1) — \beta k P(x(t)=k) \end{aligned}$$
Добавляя эффект восстановления, получаем
$$\begin{aligned} \frac{d}{dt}P(x (t)=k)= & {} \beta (k-1) P(x(t)=k-1) — (\gamma +\beta ) k P(x(t)=k) + \gamma ( k+1) P(x(t)=k+1) \end{aligned}$$
, где \(\gamma\) — индивидуальная скорость восстановления.В целом это можно резюмировать с помощью CTMC, изображенного на рис. 5.
Рисунок 5Цепь Маркова с непрерывным временем для зараженных кластера 5.
Таким образом, количество инфицированных людей в условиях эпидемии можно смоделировать как цепь Маркова с непрерывным временем (ЦВМК) \(\{x_t, \; t\ge 0\}\), с пространством состояний \(X=\{ 0,1,2,\dots ,N\}\) и инфинитезимальный генератор Q , где Q — матрица с элементами, для \(i,j\in \{1,2,3,\dots ,N\ }\),
$$\begin{aligned} q_{ij}= & {} \left\{ \begin{array}{ll} i\beta &{} j = i+1 \\ i\gamma & {} j = i-1 \\ -i(\gamma +\beta ) &{} j=i\\ 0 &{} \text{ Иначе. } \end{массив} \right. \end{aligned}$$
} \end{массив} \right. \end{aligned}$$
Теперь мы можем смоделировать ежедневное количество инфицированных в популяции как дискретную выборку CTMC \(\{x(n),\; n=0,1,2,\dots \}\ ), с пространством состояний \(X=\{0,1,2,\dots ,N\}\) и вероятностями перехода
$$\begin{aligned} x_0\sim & {}\, P_0\\ p( x_k|x_{1:(k-1)})= & {} \,H_{x_{k-1},x_k},\;k=1,2,3,4,\dots ,\\ \end {выровнено}$$
, где \(P_0 = (p(x_0=0),p(x_0=1),\dots ,p(x_0=N))\) — начальное распределение \(x_0\) и \(H_{x_{k-1},x_k}\) — это \(x_{k-1},x_k\)-й элемент матрицы \(H = \exp (Q \ dT)\), причем dT – период выборки.
Присутствие переданного вируса среди людей сначала выявляется с помощью начальной выборки результатов тестирования \(y_0\). Следовательно, начальные условия для байесовского фильтра можно найти из
$$\begin{aligned} p(x_0|y_0) = \frac{p(y_0 | x_0)p(x_0)}{p(y_0)}. \end{выровнено}$$
(3)
В большинстве случаев, если нет начальных данных для \(x_0\), то мы можем (используя принцип максимальной энтропии) априори предположить, что \(x_0\) равномерно распределено на некотором интервале, т. е.g, \(\{0,..,N\}\) (обозначено как единообразное в сопровождающем R-скрипте). Другая возможность состоит в том, чтобы выбрать \(x_0\) для любого усеченного дискретного распределения с поддержкой множества \(\{0,1,2,\dots,N\}\), например распределение Пуассона (выдуманное распределение Пуассона в сопровождающем R-скрипте). Наконец, если мы точно знаем начальное количество инфицированных, мы можем выбрать это число с вероятностью один. Условное распределение \(p(y_0|x_0)\) в уравнении. (3) можно рассчитать с помощью приближений, описанных в разделе «Наблюдательная модель».
е.g, \(\{0,..,N\}\) (обозначено как единообразное в сопровождающем R-скрипте). Другая возможность состоит в том, чтобы выбрать \(x_0\) для любого усеченного дискретного распределения с поддержкой множества \(\{0,1,2,\dots,N\}\), например распределение Пуассона (выдуманное распределение Пуассона в сопровождающем R-скрипте). Наконец, если мы точно знаем начальное количество инфицированных, мы можем выбрать это число с вероятностью один. Условное распределение \(p(y_0|x_0)\) в уравнении. (3) можно рассчитать с помощью приближений, описанных в разделе «Наблюдательная модель».
Таким образом, мы можем проиллюстрировать структуру зависимостей Скрытой марковской модели на рис. 6.
Рис. 6Структура зависимостей байесовского фильтра.
Модель наблюдения
Обычно модель эпидемии не наблюдается, но каждый день несколько человек проверяются на наличие инфекции, а ряд положительных образцов секвенируется для классификации образцов по вариантам. Из секвенированных образцов записывают номер данного варианта. Предполагая, что количество размеров выборки PCR и WGS, \(n_k\) и \(m_k\), известно, схема последовательной выборки может быть сформулирована в виде иерархической модели следующим образом:
Из секвенированных образцов записывают номер данного варианта. Предполагая, что количество размеров выборки PCR и WGS, \(n_k\) и \(m_k\), известно, схема последовательной выборки может быть сформулирована в виде иерархической модели следующим образом:
$$\begin{ выровнено} z_k,z’_k|x_k,x’_k\sim & {} \text{ Гипергеометрическое}(N,x_k,x’_k,n_k), \end{выровнено}$$
(4)
$$\begin{align} y_k|z_k,z’_k\sim & {} \text{Гипергеометрический}(z_k+z’_k,z_k,m_k).{\ мин (x’_k, n_k-i)} p (y_k | z_k = i, z’_k = j) p (z_k = i, z’_k = j | x_k, x_k’). \end{выровнено}$$
(6)
Однако из-за вычислительной сложности задействованных биномиальных коэффициентов мы ищем аппроксимации (6). Для заданных размеров популяции и уровня инфицирования можно было бы ожидать приближения Пуассона к \(y_k|x_k,x_k’\) со средним значением, соответствующим отношению конкретного варианта в популяции, \(x_k/(x_k+x ‘_k)\), умноженный на размер выборки \(m_k\), обеспечит хорошее приближение распределения \(y_k|x_k,x_k’\), т. е.е.
е.е.
$$\begin{aligned} E[y_k|x_k,x_k’]= & {} m_k\frac{x_k}{x_k+x’_k}, \end{aligned}$$
что приводит к следующему Аппроксимация распределения Пуассона (Пуассона)
$$\begin{aligned} y_k|x_k,x_k’ \sim \text{ Pois }\left( m_k\frac{x_k}{x_k+x_k’}\right) . \end{aligned}$$
и следующее приближение биномиального распределения (Binom1)
$$\begin{aligned} y_k|x_k,x_k’ \sim \text{ Binom }\left( m_k,\frac{x_k} {x_k+x_k’}\справа) . \end{aligned}$$
и следующее приближение биномиального распределения (Binom2) на основе соотношений
$$\begin{aligned} y_k|x_k,x_k’ \sim \text{ Binom }\left( p_k n_k,\ frac{x_k}{N}\right) .\end{aligned}$$
Мы смоделировали 10 000 реализаций \(y_k\) из двухступенчатой выборки, с \(N=600 000\), \(x_k=3 312\), \(x_k’=288 \), \(n_k=17 000\) и \(m_k=29\), и построил аппроксимацию выборочного распределения по относительным частотам. Затем мы сравнили приближения Пуассона, Бинома1 и Бинома2 с аппроксимированным распределением выборки по расстоянию Кульбака-Лейблера, см.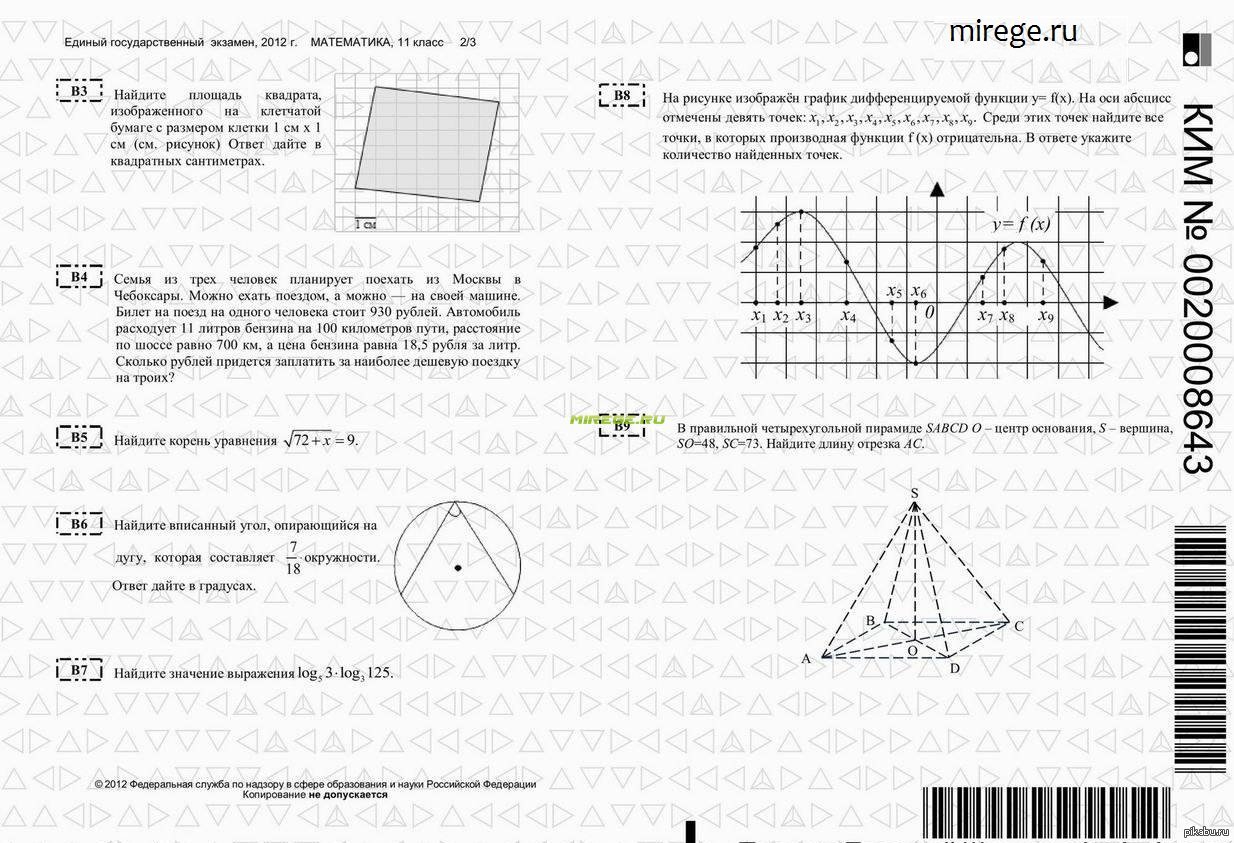 2}{2} \end{aligned}$$
2}{2} \end{aligned}$$
(7)
В приведенных выше симуляциях мы имеем \(\lambda _1=2.32\). Если мы подставим это в (7) вместе с смоделированным KLD, мы получим \(\эпсилон =0,042\) и \(\лямбда _2=2,42\), иллюстрирующие близость приближения Пуассона.
Оценка текущего номера конкретного варианта
Основной вопрос статьи состоит в том, чтобы оценить распределение текущего номера конкретного варианта по прошлым и текущим наблюдениям за вариантом, т.е. задача состоит в том, чтобы найти \( p(x_k|y_0,\dots,y_k)\).
Этого можно добиться с помощью традиционного рекурсивного байесовского фильтра с начальным значением
$$\begin{aligned} p(x_0|y_0) \propto p(y_0|x_0)p(x_0) \end{aligned}$$
(8)
и
$$\begin{align} p(x_k|y_0,\dots ,y_k) \propto p(y_k|x_k)\sum _{x_{k-1}}p(x_k|x_{k- 1})p(x_{k-1}|y_0,\dots ,y_{k-1}).\end{выровнено}$$
(9)
для \(k=1,2,3,\dots\). Заметим, что все значения рекурсии в (8) и (9) были указаны выше в модели эпидемии и модели наблюдения.
Заметим, что все значения рекурсии в (8) и (9) были указаны выше в модели эпидемии и модели наблюдения.
| Раздел | Комплект оборудования | записка себе из срок | ||
| Домашнее задание из главы 1 и главы 2 | ||||
| 3.1 | RE: §3.1 Групповая работа. См. страницу Piazza вашей группы, чтобы найти шаблон LaTex для теоремы вашей группы. | |||
| 3.1 | Вт 28 сентября | К началу занятий разместите на странице вашей группы на Piazza доказательства того, что
ваша группа начала обсуждение § 3.1 Групповая работа. Это свидетельство
может быть в виде
загрузил первый черновик вашего доказательства (в виде файла PDF) или
(как минимум) твое фото
группа «Земля мыслей» (можно фото с мобильного телефона).Если у вас есть какие-либо вопросы, просто напишите мне.
| ||
| 3.1 | Чт 9/30 | Каждая группа должна принести достаточное количество копий своих Окончательная версия § 3.1 Групповая работа , чтобы у каждого человека в комнате распечатка (в комнате 18 человек). Если вы пошлете профессору Жирарди PDF-файл с вашей окончательной версией до среды 29 сентября в 17:00, она сделает копии для ваша группа. | ||
| 3.1 | 6 | Вт 05.10 |
Этот набор HW
файл LaTeX и соответствующий
PDF-файл. Варианты (и подсказки) смотрите в приведенном выше PDF-файле этого HW Set)
| |
| 3.1 и 3.2 | 7 | Чт 21. 10. 10.
|
Этот набор HW
файл LaTeX и соответствующий
PDF-файл. Варианты (и подсказки) смотрите в приведенном выше PDF-файле этого HW Set.
| |
| 3.2 | 8 | Чт 28.10. |
Этот набор HW
файл LaTeX и соответствующий
PDF-файл. Варианты (и подсказки) смотрите в приведенном выше PDF-файле этого HW Set.
| |
| 3,3 и 5,1 и 5,5 | 9 | Т 11/4 |
Этот набор HW
файл LaTeX и соответствующий
PDF-файл. Варианты (и подсказки) смотрите в приведенном выше PDF-файле этого HW Set.
| |
| 4.1 | Вт 9 ноября | Напомним, как было объявлено в классе в четверг. 11/4 (в конце, вместо обычного начала) Викторина по учебному пособию во вторник, 9 ноября, будет охватывать § 4.1, а также первые два Скринкасты из §4.1. | ||
| 3,4 и 3,5 | 10 | Чт 11/11 |
PDF-файл.
Файл LaTeX.
Варианты (и подсказки) см. в PDF-файле этого HW Set.
| |
| 3.6 Группа | Сб 13.11 в 23:59 |
Задачи с подсказками.
Файл Latex, без подсказок.
Каждая группа должна решить обе задачи.
Работа должна быть LaTexed.
Каждая группа должна отправить по электронной почте PDF-файл своей работы.
Это должно произойти в субботу, 13 ноября, в 23:59.
Пьяцца настроена с новыми группами. Эта групповая работа стоит
два (по 5 баллов каждый) проверок прогресса .
Проблема 1.Хорошее решение:
З.
Прочитайте комментарии к этим другим документам:
ИКС ,
ИКС ,
ИКС .
Оценочная работа вашей группы находится на Piazza (в папке «групповая работа»). | 4.1 | 11 | Вт 16.11. |
PDF-файл.
Файл LaTeX.
Варианты (и подсказки) см. в PDF-файле этого HW Set.
Отзыв грейдера:
Основная проблема, которую я заметил, заключалась в том, что многие студенты до сих пор не включили базовый случай в задачу 52. Пара других студентов мучилась с тем, как доказать, что базовый случай верен или нет. |
| 4,2 и 4,3 | Чт 18/11 | Учебное пособие Викторина. | ||
| Экзамен2 Практика Задачи |
вместо до превратить в |
Раздел 3.6 называется соответствующим образом Обзор методов доказательства .
В каждом разделе гл. 3, вы узнали некоторые методы доказательств.Теперь книга бросает целую кучу упражнений на то, вы и
просит вас подтвердить их (но не указывает, какой метод подтверждения
использовать). Поэтому вам нужно выбрать, какой метод использовать, а затем выполнить
метод должным образом. Иногда работают несколько методов, но определенный метод
намного проще, чем другие методы. Иногда используется только один метод
выполнимо, учитывая то, что вы уже знаете в своей математической карьере.
§3.6 — отличный источник экзаменационных задач.
Вы должны уметь решать следующие задачи, когда
вы подходите к Экзамену 2 (а также можете написать каждый символически
но сдавать их пока не нужно):
*Подсказка на 3.6.1. Символически выглядит так
(∀ x∈ ℝ) (∀ y∈ ℝ)
[ P(x,y) ⇒ Q(x,y) ], где P(x,y) и Q(x,y)
— открытые предложения (здесь они будут неравенствами) от переменных x и y.
Раздел 4.1 (Введение в базовую математику) также будет включен в Экзамен 2. Практические задачи: Б1 , Б2 , Б3 . Попробуйте решить эти 3 задачи, прежде чем смотреть образец решения. Раздел 3.1 (Прямые доказательства) находится на экзамене 2 (и также был на экзамене 1). Экзамен 1 Практические задачи (А) — (I) — хорошие задачи. Кроме того, некоторые решения/подсказки для практических задач. Классу предлагается обсудить эти проблемы (на сайте класса Piazza есть экзаменационная папка). Поскольку эти проблемы не подлежат передаче, не стесняйтесь публиковать свои решения на Piazza. (можно просто выложить фото с мобильного телефона). |
||
| 4.2 | Вт 30.11 |
Напомним, электронное письмо, отправленное в четверг 18 ноября, о задании по чтению на вторник.11/30. Это задание по чтению необходимо для понимания лекции во вторник. Ниже приведено основное содержание письма.  PDF-файл здесь имеет, для второго примера сильной индукции из класса перед экзаменом, имеет
| ||
| 4,2 и 4,3 | 12 | Вт 30.11 |
PDF-файл.
Файл LaTeX.
Варианты (и подсказки) см. в PDF-файле этого HW Set.
Решения:
53 и
54. |
|
Математика 172 : Промежуточный курс 1 — Математика 172 — Расчет II
Вторник, 5 февраля: 18:10–20:00 |
|||
| 1) |
Приблизительно 40% экзамена будут связаны с проблемами интеграции
Для обратного триггера. интегралы (5.8) вам нужно будет запомнить:
|
||
| 2) | Баланс экзамена будет по интегральным приложениям
Вам нужно будет выполнить одно из пяти действий, описанных выше. В некоторых случаях вас попросят только «подставить» интеграл, что означает выписать определенное интеграл с правильными пределами интегрирования и правильным подынтегральным выражением. |
||
| 3) | Некоторые примечательные исключения из экзамена:
|
||
| 4) |
Ожидается, что вы вычислите sin, cos и tan кратных Pi/6, Pi/4, Pi/3, Pi/2. а также оценить обратные триггерные функции (arcsin, arccos, arctan) от 0, 1/2, sqrt(3)/2,1.х)=х, ln(e)=1 и ln(1)=0. |
||
| 5) | Экзаменационные вопросы — это варианты домашних заданий. Вообще говоря, HW очень
хорошее руководство по видам задач на тесте. Вообще говоря, HW очень
хорошее руководство по видам задач на тесте. |
||
| 6) | Если вы хорошо подготовлены, вы сможете сдать экзамен за 50 минут, но у вас будет 1 час 50 минут | ||
| 7) | Помните о наших учебных ресурсах — как Центре обучения математике, так и обзорных занятиях
принадлежит Робу Мало. |
||
TERF (CBL) — усовершенствованная технология обратного переворота (обучение на основе критериев) Обновлено: 24. 07.2015.
07.2015.
COVID-19: переход на красный уровень оповещения, изменения в экзаменах | Выписки из университетов
Уважаемое сообщество кампуса Итаки,
После нашего субботнего сообщения наши тесты наблюдения продолжали выявлять быстрое распространение COVID-19 среди наших студентов. Несмотря на то, что количество случаев заболевания преподавателей и сотрудников в настоящее время остается низким, только вчера вечером наша команда лаборатории тестирования на COVID-19 обнаружила признаки высококонтагиозного варианта Omicron в значительном количестве положительных образцов студентов, полученных в понедельник.В результате и из-за большой осторожности университет переходит на уровень оповещения Red и объявляет о ряде немедленных мер, изложенных ниже.
Я хочу пояснить, что наши доказательства существования Омикрона являются предварительными. ПЦР-тестирование выявило его отличительный признак (так называемый выпадение S-гена) в значительном количестве образцов вируса. Хотя мы должны дождаться подтверждающей информации о секвенировании, чтобы убедиться, что источником является Омикрон, мы действуем так, как если бы это было так.
ПЦР-тестирование выявило его отличительный признак (так называемый выпадение S-гена) в значительном количестве образцов вируса. Хотя мы должны дождаться подтверждающей информации о секвенировании, чтобы убедиться, что источником является Омикрон, мы действуем так, как если бы это было так.
Хотя о варианте Омикрон еще многое неизвестно, он, по-видимому, значительно более заразен, чем Дельта и другие варианты. Есть некоторые доказательства (хотя и далеко не достоверные), что он обычно вызывает более легкие случаи, особенно среди вакцинированных людей. Однако, когда у вас высокая трансмиссивность, у вас будет очень большое количество случаев, и поэтому даже при более низких показателях серьезных заболеваний к вспышкам следует относиться серьезно.
Таким образом, мы должны сделать все возможное, чтобы ограничить дальнейшее распространение, даже если до конца семестра осталось всего несколько дней.Вот почему мы переходим на красный уровень оповещения, и с этим переходом:
.
Академическое руководство:
- Все выпускные экзамены будут переведены в онлайн-формат с полудня вторника, 14 декабря. Экзамены, которые уже были переведены в онлайн-формат, будут проходить в соответствии с графиком, включая сегодняшние экзамены. Некоторые экзамены, которые все еще запланированы для личного участия, могут быть немедленно переведены в онлайн-режим; другие, возможно, придется перенести, чтобы дать преподавателям время для разворота.Пожалуйста, будьте бдительны при поиске обновлений по электронной почте от вашего факультета. Более подробная информация об экзаменах будет опубликована в разделе академической политики на веб-сайте COVID-19, как только она станет доступна.
Отмена мероприятий и влияние на кампус:
- Все университетские мероприятия с участием студентов (включая мероприятия и общественные собрания), а также все мероприятия, спонсируемые университетом (включая зимние праздники), отменены.
- Церемония награждения выпускников декабря 18 декабря отменяется.

- Учащимся, использующим Cornell Dining, настоятельно рекомендуется «брать и идти»; если вы должны есть рядом с другими, пожалуйста, делайте это на расстоянии.
- Библиотеки закрыты для студентов.
- Соревнования по легкой атлетике в воскресенье отменяются. Фитнес-центры и спортзалы закрыты для студентов.
- Офисы и лаборатории остаются открытыми , но студенты бакалавриата не должны участвовать ни в какой учебной или лабораторной работе.
Студенческие поездки и общественное здравоохранение в кампусе:
- Учащиеся с отрицательным результатом теста за последние 48 часов (суббота или воскресенье) и желающие покинуть кампус могут сделать это.Пожалуйста, всегда носите маску во время путешествия, сдайте тест на COVID-19 в пункте назначения и самоизолируйтесь, пока не получите результат.
- Все учащиеся должны заполнить контрольный список перед отъездом, прежде чем покинуть кампус.

- Любой учащийся, у которого за последние 48 часов был получен отрицательный результат теста , а не , должен как можно скорее пройти дополнительный тест. Запланируйте свой тест на www.dailycheck.cornell.edu. Студентам рекомендуется оставаться в Итаке, в своих резиденциях, до тех пор, пока не будут получены результаты их тестов, и строго ограничивать взаимодействие с другими людьми в течение этого времени.Дополнительную информацию о тестировании при отъезде, о том, как получить результаты, и о продленных часах приема можно найти в Daily Check.
- Мы продолжим помогать нашим студентам-интернатам на территории кампуса с положительным результатом теста на безопасную изоляцию на требуемый 10-дневный срок, пока они не получат разрешение от Департамента здравоохранения округа Томпкинс на безопасное путешествие.
- Посетители и гости не допускаются на территорию кампуса, за исключением тех, кто забирает студентов на перемены.В этом случае мы просим вас постоянно оставаться в маске, пока вы ненадолго находитесь в кампусе.

- Учащиеся должны избегать несущественных контактов с другими и повышать свою бдительность с помощью ношения масок, дистанцирования и мытья рук. В настоящее время более 97% наших студентов свободны от вируса, и мы хотим, чтобы каждый мог насладиться здоровыми зимними каникулами с семьей и друзьями.
Персонал и преподаватели:
- Обязательное контрольное тестирование будет продолжаться в обычном режиме для всех зарегистрированных в настоящее время сотрудников.Дополнительное тестирование будет по-прежнему доступно для всех сотрудников.
Хотя я хочу заверить вас в том, что на сегодняшний день мы не видели тяжелых заболеваний ни у одного из наших инфицированных учащихся, мы все же можем сыграть свою роль в уменьшении распространения болезни в более широком сообществе. Тот факт, что мы не сталкивались с серьезными заболеваниями среди наших студентов, может заставить некоторых задаться вопросом, почему мы навязываем такие серьезные шаги. Итак, позвольте мне поделиться базовой математикой: рассмотрим один вариант, назовем его А, в котором каждый человек заражает в среднем двух других и который вызывает серьезное заболевание в 1% случаев.После десяти итераций передачи у вас будет около 1000 случаев и 10 случаев серьезных заболеваний. Теперь рассмотрим вариант Б, который в два раза более заразен, так что каждый человек заражает в среднем четырех других, но вызывает тяжелые заболевания лишь в 10 раз реже, т. е. всего в 0,1% случаев. Без проверки, через те же десять итераций передачи, с вариантом Б у вас будет более миллиона случаев и около 1000 человек с серьезными заболеваниями. Конечно, в игру вступают и другие факторы, в том числе тот факт, что вирус «исчерпает» людей для заражения в любом сообществе, но дело в том, что более высокая трансмиссивность приводит к экспоненциальному росту, который перевешивает линейное снижение процента тяжелых случаев. .Чтобы избежать подобных ситуаций, крайне важно не оставлять такие инфекции бесконтрольными, а принимать меры, ограничивающие передачу.
Итак, позвольте мне поделиться базовой математикой: рассмотрим один вариант, назовем его А, в котором каждый человек заражает в среднем двух других и который вызывает серьезное заболевание в 1% случаев.После десяти итераций передачи у вас будет около 1000 случаев и 10 случаев серьезных заболеваний. Теперь рассмотрим вариант Б, который в два раза более заразен, так что каждый человек заражает в среднем четырех других, но вызывает тяжелые заболевания лишь в 10 раз реже, т. е. всего в 0,1% случаев. Без проверки, через те же десять итераций передачи, с вариантом Б у вас будет более миллиона случаев и около 1000 человек с серьезными заболеваниями. Конечно, в игру вступают и другие факторы, в том числе тот факт, что вирус «исчерпает» людей для заражения в любом сообществе, но дело в том, что более высокая трансмиссивность приводит к экспоненциальному росту, который перевешивает линейное снижение процента тяжелых случаев. .Чтобы избежать подобных ситуаций, крайне важно не оставлять такие инфекции бесконтрольными, а принимать меры, ограничивающие передачу.
Совершенно очевидно, что такие шаги крайне удручают. Однако с самого начала пандемии мы взяли на себя обязательство следовать науке и делать все возможное для защиты здоровья наших преподавателей, сотрудников и студентов.
За последние несколько месяцев мы вместе преодолели множество испытаний. Я уверен, что мы снова сможем справиться с этой текущей задачей, чтобы мы все могли сделать заслуженный перерыв.
С уважением,
Марта Э. Поллак
Президент
Нейробиологические причины индивидуальных различий в математических способностях
Abstract
Математические способности передаются по наследству и связаны с несколькими генами, экспрессирующими белки в головном мозге. Однако неизвестно, какие промежуточные нейральные фенотипы могут объяснить, как эти гены связаны с математическими способностями. Здесь мы исследовали генетические эффекты на объем коры головного мозга 3-6-летних детей без математической подготовки, чтобы предсказать математические способности в школе в возрасте 7-9 лет. С этой целью мы использовали исследовательскую выборку ( n = 101) и независимую повторную выборку ( n = 77). Мы обнаружили, что ROBO1 , ген, который, как известно, регулирует пренатальный рост слоев коры головного мозга, связан с объемом правой теменной коры, ключевой области для количественного представления. Индивидуальные различия в объеме в этой области предсказывали до одной пятой поведенческой дисперсии математических способностей. Наши результаты показывают, что фундаментальный генетический компонент системы обработки количества коренится в раннем развитии теменной коры.
С этой целью мы использовали исследовательскую выборку ( n = 101) и независимую повторную выборку ( n = 77). Мы обнаружили, что ROBO1 , ген, который, как известно, регулирует пренатальный рост слоев коры головного мозга, связан с объемом правой теменной коры, ключевой области для количественного представления. Индивидуальные различия в объеме в этой области предсказывали до одной пятой поведенческой дисперсии математических способностей. Наши результаты показывают, что фундаментальный генетический компонент системы обработки количества коренится в раннем развитии теменной коры.
Образец цитирования: Skeide MA, Wehrmann K, Emami Z, Kirsten H, Hartmann AM, Rujescu D, et al. (2020) Нейробиологические истоки индивидуальных различий в математических способностях. ПЛОС Биол 18(10): е3000871. https://doi.org/10.1371/journal.pbio.3000871
Академический редактор: Андреас Нидер, Университет Тюбингена, ГЕРМАНИЯ
Получено: 9 апреля 2020 г . ; Принято: 18 сентября 2020 г .; Опубликовано: 22 октября 2020 г.
Авторское право: © 2020 Skeide et al.Это статья с открытым доступом, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Все соответствующие данные содержатся в документе и в файлах вспомогательной информации. Код, сгенерированный в нашем исследовании, доступен по адресу https://github.com/SkeideLab/PLOSBio-2020.
Финансирование: Работа выполнена при поддержке гранта Общества Фраунгофера и Общества Макса Планка (М.FE.A.NEPF0001). Спонсор не участвовал в разработке дизайна исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Конкурирующие интересы: Авторы заявили об отсутствии конкурирующих интересов.
Сокращения: КПП, Набор инструментов для компьютерной анатомии; ХВЕ, Равновесие Харди-Вайнберга; ЛК, коэффициент латеральности; МАФ, частота минорного аллеля; МНИ, Монреальский неврологический институт; MP2RAGE, быстрое градиентное эхо-сигнал, подготовленный к намагничиванию; SD, среднеквадратичное отклонение; СНП, полиморфизм единичного нуклеотида; СПМ 12, Статистическое параметрическое картографирование 12; WISC-IV, Шкала интеллекта Векслера для детей
Введение
Математические способности формируются в результате сложного взаимодействия между генетическими факторами и факторами окружающей среды, при этом генетическая изменчивость объясняет около 60% поведенческой изменчивости [1].Опираясь на эти данные, было обнаружено, что несколько вариантов ДНК связаны с математическими способностями, в том числе RP11-815M8 . 1 , FLJ20160 , Robo1 , Fam43a / LSG1 , SFT2D1 , DLD , NUAKAM , Nuak1 , C14ORF64 и GRIK1 [2-5]. Многие из этих вариантов расположены на генах, которые также экспрессируют белки в ткани нервных клеток [6]. Однако мало что известно о том, как паттерны экспрессии связанных с математикой генов распределяются по развивающемуся человеческому мозгу (www.Brainspan.org). Соответственно, остается открытым вопрос, как развивающийся мозг как промежуточный фенотип может преодолеть разрыв между генетической изменчивостью и математическими способностями.
1 , FLJ20160 , Robo1 , Fam43a / LSG1 , SFT2D1 , DLD , NUAKAM , Nuak1 , C14ORF64 и GRIK1 [2-5]. Многие из этих вариантов расположены на генах, которые также экспрессируют белки в ткани нервных клеток [6]. Однако мало что известно о том, как паттерны экспрессии связанных с математикой генов распределяются по развивающемуся человеческому мозгу (www.Brainspan.org). Соответственно, остается открытым вопрос, как развивающийся мозг как промежуточный фенотип может преодолеть разрыв между генетической изменчивостью и математическими способностями.
Математическое познание опирается на разнообразные, динамически взаимодействующие нейронные системы [7]. Помимо зрительного и/или слухового аппарата, основные ресурсы обработки обеспечиваются системами внимания и исполнения префронтальной коры, премоторным механизмом репетиции кратковременной памяти, единицей хранения долговременной памяти в медиальной височной доле и, в частности, теменная кора, которая строит зрительно-пространственные количественные представления [7–11]. Таким образом, все эти анатомически широко распространенные системы могут быть связаны с ранее описанными генами, связанными с математическими способностями.
Таким образом, все эти анатомически широко распространенные системы могут быть связаны с ранее описанными генами, связанными с математическими способностями.
Цель настоящего исследования заключалась в изучении связей между известными генами-кандидатами в области математики и структурой мозга у маленьких детей, которые еще не обучались математике. Кроме того, мы долго изучали, будут ли эти ассоциации предсказывать математические успехи в школе. Нацеливание на структурную магнитно-резонансную томографию (т.е., объем серого вещества) был мотивирован имеющимися в настоящее время нейробиологическими данными для генов-кандидатов. Эти данные предоставляют сходящиеся доказательства того, что гены, связанные с математикой, играют роль в росте серого вещества, в частности, в формировании синапсов, внутрикортикальном разветвлении аксонов и миграции нейронов [12-14]. Важно отметить, что причина сосредоточения внимания на изначально не обученной выборке заключалась в том, чтобы выявить потенциальные нейробиологические предрасположенности, а не последствия индивидуального успеха в обучении математике.
В качестве первого шага нашего анализа мы выбрали 18 однонуклеотидных полиморфизмов (SNP) в 10 генах, которые, как ранее было установлено, в значительной степени связаны с математическими способностями. Ассоциации между этими SNP и объемом серого вещества были затем рассчитаны на уровне всего мозга в исследовательской выборке ( n = 101) и, руководствуясь анализом мощности, в независимой повторной выборке ( n = 77) из 3–3 6-летние дети. С этой целью мы использовали многомерную статистическую модель, определяющую совместные эффекты SNP, локализованных в одном и том же гене.В частности, мы количественно оценили ассоциации между всеми SNP, а затем связали полученную ковариационную матрицу с матрицей данных МРТ. Мы не применяли предопределенный коэффициент детерминации или пороговое значение p для предварительного выбора конкретных SNP. Было показано, что этот подход обнаруживает биологически достоверные зависимости между SNP и увеличивает статистическую мощность по сравнению с классическими одномерными подходами [15]. Наконец, в объемных кластерах, полученных из модели генетической ассоциации, мы провели многомерный анализ прожекторов для декодирования вокселов, связанных с индивидуальными результатами тестов по математике во втором классе (7–9 лет).
Наконец, в объемных кластерах, полученных из модели генетической ассоциации, мы провели многомерный анализ прожекторов для декодирования вокселов, связанных с индивидуальными результатами тестов по математике во втором классе (7–9 лет).
Следуя современному состоянию знаний о нейронных системах, способствующих математическому познанию, мы предположили, что можно ожидать значительных эффектов ассоциации и предсказания в префронтальной, премоторной, медиальной височной и нижней теменной коре.
Результаты
Описательные данные участника
Генотипы и структурное сканирование мозга были получены в возрасте 3–6 лет в исследовательской выборке ( n = 101) и в репликационной выборке ( n = 77).Стандартизированные возрастные нормированные оценки математических способностей, полученные в возрасте 7–9 лет, были доступны для n = 84 из 101 ребенка в исследовательской выборке и для n = 75 из 77 детей в повторной выборке. Демографические характеристики и результаты поведенческих тестов существенно не отличались между теми детьми, которые завершили обе волны сбора данных, и теми детьми, которые выбыли после первой волны сбора данных (исследуемая выборка: все z < 2, все χ < 1, все P > 0.05; повторная выборка: все z < 2, все χ < 1, все P > 0,05). Характеристики выборки на основе полных наборов данных приведены в таблице 1.
Демографические характеристики и результаты поведенческих тестов существенно не отличались между теми детьми, которые завершили обе волны сбора данных, и теми детьми, которые выбыли после первой волны сбора данных (исследуемая выборка: все z < 2, все χ < 1, все P > 0.05; повторная выборка: все z < 2, все χ < 1, все P > 0,05). Характеристики выборки на основе полных наборов данных приведены в таблице 1.
Связь между генами-кандидатами математических способностей и объемом серого вещества в возрасте 3–6 лет
В исследовательской выборке для гена ROBO1 (макс. R 2 = 0,47) (рис. 1А), но ни один из других девяти протестированных генов (таблица 2). Достигнутая мощность для обнаружения этого большого эффекта составила 0,94. Размер выборки, необходимый для воспроизведения этого эффекта со степенью 0,8, составлял 90 758 n 90 759 = 71. Соответственно, в независимой выборке из 90 758 n 90 759 = 77 эффект ассоциации 90 758 ROBO1 90 759 был воспроизведен при тестировании того же набора генов (табл. 2) при том же статистическом пороге (макс. R 2 = 0,43) (рис. 1А).Влияние возраста, пола, рук и общего внутричерепного объема контролировалось в моделях.
2) при том же статистическом пороге (макс. R 2 = 0,43) (рис. 1А).Влияние возраста, пола, рук и общего внутричерепного объема контролировалось в моделях.
Рис. 1. Объем серого вещества правой теменной коры у детей 3-6 лет без математической подготовки ассоциирован с геном коркового роста ROBO1 .
(A) Внешние угловые точки изображают 10 известных математических генов-кандидатов и соответствующие им пронумерованные хромосомы. Пунктирные линии отображают статистику R 2 , определяющую силу связи между генами и объемными изображениями серого вещества.Чем дальше точка от центра, тем сильнее ассоциация. Оранжевые точки/линии относятся к исследовательскому образцу, а синие точки/линии относятся к повторному образцу. (B-D) Правая сагиттальная проекция на проекцию поверхности коры P изображений, показывающая правые теменные кластеры, которые были в значительной степени связаны с ROBO1 . Результаты показаны отдельно для исследовательского образца (B), повторного образца (C) и перекрытия между двумя образцами (D). Цветная полоса указывает диапазон значений P с нижним порогом P < 0,05 и верхним порогом P < 0,01, с поправкой на семейную ошибку для количества протестированных вокселов и генов. Числовые данные, используемые на этом рисунке, включены в данные S1.
Цветная полоса указывает диапазон значений P с нижним порогом P < 0,05 и верхним порогом P < 0,01, с поправкой на семейную ошибку для количества протестированных вокселов и генов. Числовые данные, используемые на этом рисунке, включены в данные S1.
https://doi.org/10.1371/journal.pbio.3000871.g001
Ассоциации на уровне всего мозга считались значимыми, когда локальные кластеры оставались ниже произвольно определенного порога высоты P < 0.05 (с исправлением семейных ошибок для количества проверенных вокселей и генов) и превысило произвольный порог экстента k > 100 вокселей. В контрольной выборке эффект ROBO1 локализовался в правой теменной коре, охватывающей дорсальную губу внутритеменной борозды, переходящей в прилежащую извилину вентральной верхней теменной дольки (координаты пика MNI: +45–33 +57; k = 437 вокселей) (рис. 1B). Никакие другие области не превышали порог пространственной протяженности k = 100 вокселей. В повторном образце эффект ROBO1 также был локализован в правой теменной коре (координаты пика MNI: +49–41 +55; k = 304 вокселя), где оба кластера перекрывались (рис. 1C и 1D).
В повторном образце эффект ROBO1 также был локализован в правой теменной коре (координаты пика MNI: +49–41 +55; k = 304 вокселя), где оба кластера перекрывались (рис. 1C и 1D).
Прогноз успеваемости по математике в возрасте 7–9 лет по объему теменного серого вещества в возрасте 3–6 лет
Индивидуальный объем серого вещества в правом теменном кластере, который был связан с ROBO1 в возрасте 3–6 лет, был в значительной степени связан с индивидуальными баллами в комплексном поведенческом математическом тесте, проведенном в возрасте 7–9 лет.Связи были значимыми при пороге P <0,05 (тест перестановки с поправкой на количество протестированных вокселей) в исследовательской выборке (макс. R 2 = 0,10) (рис. 2A) и репликационной выборке (рис. 2A). макс R 2 = 0,22) (рис. 2В) в перекрывающейся части правой теменной коры (рис. 2С). Дополнительные отдельные анализы ассоциаций поведения мозга и поведения не выявили свидетельств диссоциации между умением считать и вычислительными навыками в исследовательской выборке ( z = 0. 23, P = 0,410) и повторный образец ( z = 0,40, P = 0,343). В моделях контролировалось влияние возраста, пола, руки, общего внутричерепного объема, образования матери и невербального IQ.
23, P = 0,410) и повторный образец ( z = 0,40, P = 0,343). В моделях контролировалось влияние возраста, пола, руки, общего внутричерепного объема, образования матери и невербального IQ.
Рис. 2. ROBO1 -ассоциированный объем серого вещества правой теменной коры у детей 3–6 лет без математической подготовки прогнозирует математические способности в школе в возрасте 7–9 лет.
(A–C) Правый сагиттальный вид на проекцию поверхности коры P -value изображений, показывающих воксели в теменных кластерах, которые были значительно связаны с ROBO1 в возрасте 3–6 лет и с индивидуальными оценками математических способностей Тест проводится в возрасте 7-9 лет.Результаты показаны отдельно для контрольного образца (A), повторного образца (B) и перекрытия между двумя образцами (C). Цветная полоса указывает диапазон значений P с нижним порогом P < 0,05 и верхним порогом P < 0,01 (с поправкой на перестановку по вокселям). Числовые данные, используемые на этом рисунке, включены в данные S2.
Числовые данные, используемые на этом рисунке, включены в данные S2.
https://doi.org/10.1371/journal.pbio.3000871.g002
Обсуждение
В этом исследовании мы изучили ассоциации между 18 SNP на 10 генах-кандидатах в области математики и объемом серого вещества всего мозга в исследовательской выборке из 101 и повторной выборке из 77 детей, не посещающих школу, в возрасте 3–6 лет.Мы наблюдали, что ген ROBO1 был значительно связан с объемом серого вещества в дорсальных отделах правой внутритеменной борозды и вентральных отделах правой верхней теменной дольки. Структура объема серого вещества в этих областях выявила значительную связь с результатами тестов по математике в возрасте 7–9 лет во втором классе.
Роль
ROBO1 для развития серого вещества Сообщаемая связь между ROBO1 и объемом серого вещества подтверждается большим объемом литературы по молекулярной генетике, предполагающей, что этот ген играет решающую роль в пренатальном росте неокортекса грызунов. В частности, имеются сходящиеся данные о том, что ROBO1 регулирует миграцию нейронов (т.е. расположение нейронов в слоях коры во время внутриутробного созревания мозга) [13, 16, 17]. Более того, ROBO1 также может способствовать пролиферации нейронов в коре [18].
В частности, имеются сходящиеся данные о том, что ROBO1 регулирует миграцию нейронов (т.е. расположение нейронов в слоях коры во время внутриутробного созревания мозга) [13, 16, 17]. Более того, ROBO1 также может способствовать пролиферации нейронов в коре [18].
Данные об экспрессии генов человека, собранные ex vivo, подтверждают нейроанатомическую достоверность эффекта, который мы обнаружили здесь in vivo. Эта работа демонстрирует, что белки, кодируемые ROBO1 , последовательно экспрессируются в теменной коре двух 3-летних и двух 8-летних детей (www.Brainspan.org). Наши результаты, однако, не позволяют нам делать какие-либо твердые выводы об отрицательных результатах в других областях.
ROBO1 , теменная кора и математические способности
Текущие результаты предполагают, что индивидуальные различия в росте правой теменной коры могут быть промежуточным фенотипом, заполняющим объяснительный пробел в ранее сообщавшихся связях между вариациями ДНК и поведенческими математическими способностями. Эта интерпретация согласуется с многочисленными исследованиями, показывающими, что теменная кора специфически способствует математическому познанию с детства и сохраняет эту решающую роль во взрослом возрасте [19, 20].В частности, внутритеменная борозда и верхняя теменная долька обеспечивают нейронные ресурсы для определения количества, которое остается важным базовым компонентом даже для решения математических задач более высокого порядка [20].
Эта интерпретация согласуется с многочисленными исследованиями, показывающими, что теменная кора специфически способствует математическому познанию с детства и сохраняет эту решающую роль во взрослом возрасте [19, 20].В частности, внутритеменная борозда и верхняя теменная долька обеспечивают нейронные ресурсы для определения количества, которое остается важным базовым компонентом даже для решения математических задач более высокого порядка [20].
Интересно, что навыки обработки несимволических величин обычно появляются в первые месяцы жизни без формального образования и проявляют заметные индивидуальные различия с самого начала онтогенеза [21]. По результатам настоящего исследования мы выдвигаем рабочую гипотезу о том, что даже эти очень ранние различия уже могут быть объяснены различиями в объеме правой теменной коры, связанными с вариабельностью ROBO1 .Для подтверждения этой гипотезы необходимы дальнейшие эксперименты с младенцами.
Полушарная специализация теменной коры
Во взрослом мозге функциональная активация во время математической обработки постоянно наблюдается в билатеральной теменной коре [22, 23]. В отличие от этого и в соответствии с нашими структурными данными, согласно недавнему метаанализу, дети активнее задействуют правую (по сравнению с левой) теменную кору при выполнении математических задач [24].Более глубокое понимание этой разницы в развитии, которая, по-видимому, исчезает с дальнейшим опытом, остается задачей будущего.
В отличие от этого и в соответствии с нашими структурными данными, согласно недавнему метаанализу, дети активнее задействуют правую (по сравнению с левой) теменную кору при выполнении математических задач [24].Более глубокое понимание этой разницы в развитии, которая, по-видимому, исчезает с дальнейшим опытом, остается задачей будущего.
Заключение
Наше исследование показывает, что до одной пятой дисперсии математических способностей можно предсказать по ранним индивидуальным различиям в объеме правой теменной коры, что связано с геном роста коры ROBO1 . Эти результаты показывают, что генетическая изменчивость может формировать математические способности, формируя раннее развитие основной системы обработки данных мозга.
Методы
Участники
Участники были набраны в период с 2012 по 2013 год, в основном из столичного региона Лейпцига, но также и из других частей Германии. Мы побудили семьи принять участие в исследовании, сказав им, что текущее исследование улучшит наше понимание происхождения нарушений обучения, связанных с развитием. Все родители или опекуны дали письменное информированное согласие, и все дети дали устное информированное согласие на участие. Участие было вознаграждено «дневником младшего научного сотрудника» и небольшим образовательным подарком для каждого ребенка, а также возмещением затрат на сеанс МРТ (15 евро) и сеансы оценки поведения (7 евро).50). Исследование было одобрено Этическим комитетом Лейпцигского университета, Германия (номер разрешения 320-11-26092011). Участники были исключены из дальнейшего анализа, если они (A) имели в анамнезе неврологические и/или психические расстройства, (B) имели нарушения слуха и/или зрения, (C) страдали синдромом дефицита внимания и гиперактивности, (D) набрали более двух стандартных баллов. отклонения (SD) ниже среднего возраста в невербальном тесте IQ и, таким образом, соответствовали критерию умственной отсталости, (E) не соответствовали экспериментальным процедурам на тренировке и/или (F) перемещались в сканере так, чтобы данные качество было скомпрометировано.
Все родители или опекуны дали письменное информированное согласие, и все дети дали устное информированное согласие на участие. Участие было вознаграждено «дневником младшего научного сотрудника» и небольшим образовательным подарком для каждого ребенка, а также возмещением затрат на сеанс МРТ (15 евро) и сеансы оценки поведения (7 евро).50). Исследование было одобрено Этическим комитетом Лейпцигского университета, Германия (номер разрешения 320-11-26092011). Участники были исключены из дальнейшего анализа, если они (A) имели в анамнезе неврологические и/или психические расстройства, (B) имели нарушения слуха и/или зрения, (C) страдали синдромом дефицита внимания и гиперактивности, (D) набрали более двух стандартных баллов. отклонения (SD) ниже среднего возраста в невербальном тесте IQ и, таким образом, соответствовали критерию умственной отсталости, (E) не соответствовали экспериментальным процедурам на тренировке и/или (F) перемещались в сканере так, чтобы данные качество было скомпрометировано. Данные были собраны в период с 2012 по 2019 год. Все эти процедуры соответствуют соответствующим этическим нормам, указанным в Хельсинкской декларации.
Данные были собраны в период с 2012 по 2019 год. Все эти процедуры соответствуют соответствующим этическим нормам, указанным в Хельсинкской декларации.
Генотипирование
ДНК из слюны экстрагировали с использованием стандартных процедур, описанных в [25], или с использованием наборов Oragene DNA Genotek (Каната, Онтарио, Канада). В исследовательском образце генотипирование всех SNP, кроме rs331142, rs12495133 и rs1995402, выполняли с помощью микрочипа Infinium HumanCoreExome Psych Chip.Генотипирование шариковых чипов проводилось в соответствии с инструкциями производителя и анализировалось с использованием модуля генотипирования GenomeStudio компании Illumina. Варианты rs331142, rs12495133 и rs1995402 были генотипированы с помощью времяпролетной масс-спектрометрии с матричной лазерной десорбцией/ионизацией (iPLEX, Agena, Гамбург, Германия). Мы наблюдали высокую степень соответствия для дополнительных SNP, генотипированных с помощью обеих технологий (99,99%). В образце репликации все варианты были генотипированы с помощью времяпролетной масс-спектрометрии с лазерной десорбцией/ионизацией на матрице (iPLEX, Agena, Гамбург, Германия).
Данные генотипирования должны были соответствовать следующим показателям качества: точное равновесие Харди-Вайнберга (HWE) по SNP P > 0,05 [26], частота вызовов по SNP > 95%, частота вызовов по отдельным случаям > 90%, MAF >0,05 и 100% соответствие между генотипами индивидуумов, которые были измерены в дубликатах. Был включен один вариант (rs363449) с отклонением от HWE ( p = 0,004), так как не было несоответствия между генотипированными центральноевропейскими трио (Институт медицинских исследований Кориелла, Камден, Нью-Джерси, США) и HapMap. база данных (https://www.ncbi.nlm.nih.gov/probe/docs/projhapmap/).
SNP, не охваченных непосредственно генотипированием, были заменены соответствующим прокси, выявляющим наибольшее неравновесие по сцеплению ( R 2 ) с исходным SNP (таблица 2) с использованием 1000 Genomes версии 1 фазы 3 в качестве эталонной панели [27]. Следует отметить в качестве ограничения, что rs4677854 не может рассматриваться как хороший прокси для rs789859, учитывая R 2 0,58.
Родство между проанализированными участниками оценивалось путем анализа показателей родства (СРК) между участниками с использованием R и GenABEL (28).Мы идентифицировали пять братьев и сестер (ожидаемый СРК = 0,5), используя общепринятое пороговое значение 0,354 (среднее геометрическое 0,5 и 0,25), и одну пару двоюродных братьев и сестер (ожидаемый СРК = 0,125), используя общепринятое пороговое значение 0,088 (рассчитано соответственно), в то время как остальные участники не были связаны между собой (СРК ≤ 0,088). Соответственно, мы также провели анализ ассоциации ген-мозг без пяти братьев и сестер и одного двоюродного брата. Этот повторный анализ воспроизвел идентичные координаты пика MNI (+45–33 +57) и статистику во всех 437 вокселях.
Сбор и предварительная обработка данных МРТ
Т1-взвешенных трехмерных изображений градиентного эха с быстрым получением данных, подготовленных к намагничиванию (MP2RAGE) [29] были получены на магнитно-резонансном сканере всего тела Siemens TIM Trio 3,0 Тесла с использованием 12-канальной радиочастотной катушки для головы и следующих параметры: TR = 5000 мс, TE = 2,82 мс, TI 1 = 700 мс, TI 2 = 2500 мс, FOV = 256 x 240, размер матрицы = 250 x 219 x 144 и размер вокселя = 1,3 x 1,3 x 1. 3 мм 3 .
3 мм 3 .
Качество изображения оценивалось с помощью двухэтапной процедуры. На первом этапе путем визуального осмотра мы убедились, что каждое изображение не содержит артефактов и/или анатомических аномалий. На последнем этапе качество изображения оценивалось автоматически путем количественного определения шума и неоднородности с использованием набора инструментов вычислительной анатомии (CAT) (http://dbm.neuro.uni-jena.de/cat), реализованного в пакете Statistical Parametric Mapping 12 (SPM 12). программное обеспечение (http://fil.ion.ucl.ac.uk/spm/). Только изображения с оценкой не менее 80 (указывающей на хорошее качество) были сохранены для дальнейшего анализа.
Объемные изображения серого вещества были рассчитаны с помощью анализа морфометрии на основе вокселей в CAT и SPM 12. С этой целью мы сначала создали индивидуальную карту вероятностей мультитканей (включая серое вещество, белое вещество, спинномозговую жидкость, кости, мягкие ткани и air/background) с помощью Template-O-Matic Toolbox (https://irc. cchmc.org/software/tom.php), используя в качестве основы набор данных, полученный в ходе МРТ-исследования нормального развития мозга NIH. Эта карта соответствовала возрасту и полу настоящего образца и служила предварительным расчетом шаблона для конкретного образца в пространстве Монреальского неврологического института (MNI) с использованием алгоритма диффеоморфной анатомической регистрации с помощью алгоритма экспоненциальной алгебры Ли.Затем мы нормализовали каждое отдельное Т1-взвешенное изображение к шаблону, специфичному для образца, и сегментировали его на серое вещество, белое вещество, спинномозговую жидкость, твердую мозговую оболочку, мягкие ткани и воздух. На основании этих данных мы смогли оценить общий внутричерепной объем. Затем были рассчитаны объемные изображения серого вещества при модуляции нелинейных эффектов, чтобы сохранить локальные объемные значения. Эти изображения, наконец, были сглажены с помощью 8-мм полной ширины с полумаксимальным ядром Гаусса.
cchmc.org/software/tom.php), используя в качестве основы набор данных, полученный в ходе МРТ-исследования нормального развития мозга NIH. Эта карта соответствовала возрасту и полу настоящего образца и служила предварительным расчетом шаблона для конкретного образца в пространстве Монреальского неврологического института (MNI) с использованием алгоритма диффеоморфной анатомической регистрации с помощью алгоритма экспоненциальной алгебры Ли.Затем мы нормализовали каждое отдельное Т1-взвешенное изображение к шаблону, специфичному для образца, и сегментировали его на серое вещество, белое вещество, спинномозговую жидкость, твердую мозговую оболочку, мягкие ткани и воздух. На основании этих данных мы смогли оценить общий внутричерепной объем. Затем были рассчитаны объемные изображения серого вещества при модуляции нелинейных эффектов, чтобы сохранить локальные объемные значения. Эти изображения, наконец, были сглажены с помощью 8-мм полной ширины с полумаксимальным ядром Гаусса.
Данные об образовании матери
Материнское образование оценивалось с помощью индивидуальной внутренней анкеты и определялось как сумма школьного образования и профессионального образования. Школьное образование оценивалось по шкале от 0 до 3 (0 = отсутствие окончания школы, 1 = окончание через 9 лет (нем. Hauptschulabschluss), 2 = окончание через 10 лет (нем. Mittlere Reife), 3 = окончание средней школы). ). Высшее образование оценивалось по шкале от 0 до 4 (0 = отсутствие профессиональной степени, 1 = профессиональная степень, 2 = степень университета прикладных наук, 3 = высшее образование, 4 = ученая степень). Согласно этой шкале индекс 4,5 представляет собой средний уровень образования матери.Таким образом, средние значения индекса текущих выборок (исследовательская выборка: 4,42, повторная выборка: 4,87) указывают на средний уровень образования матерей, варьирующийся от малообразованных до высокообразованных матерей (значения индекса 2–7).
Школьное образование оценивалось по шкале от 0 до 3 (0 = отсутствие окончания школы, 1 = окончание через 9 лет (нем. Hauptschulabschluss), 2 = окончание через 10 лет (нем. Mittlere Reife), 3 = окончание средней школы). ). Высшее образование оценивалось по шкале от 0 до 4 (0 = отсутствие профессиональной степени, 1 = профессиональная степень, 2 = степень университета прикладных наук, 3 = высшее образование, 4 = ученая степень). Согласно этой шкале индекс 4,5 представляет собой средний уровень образования матери.Таким образом, средние значения индекса текущих выборок (исследовательская выборка: 4,42, повторная выборка: 4,87) указывают на средний уровень образования матерей, варьирующийся от малообразованных до высокообразованных матерей (значения индекса 2–7).
Поведенческое тестирование
Рукоятие измерялось с помощью индивидуального внутреннего теста, в котором детей просили выполнять или имитировать повседневные действия руками, чтобы мы могли рассчитать коэффициент латеральности (LQ). Праворукость определялась как LQ > +48, леворукость — как LQ ≤ -28, амбидекстрия — как -28 < LQ ≤ +48.
Праворукость определялась как LQ > +48, леворукость — как LQ ≤ -28, амбидекстрия — как -28 < LQ ≤ +48.
Подшкала «Перцептивное мышление» Шкалы интеллекта Векслера для детей (WISC-IV) использовалась для получения оценки невербального IQ (https://www.testzentrale.de/shop/wechsler-intelligence-scale-for-children-deutsche- ausgabe-четвертое-издание.html).
Математические способности оценивались с помощью Гейдельбергского арифметического теста (https://www.testzentrale.de/shop/heidelberger-rechentest.html). Этот комплексный тестовый инструмент состоит из 11 подтестов, охватывающих сложение, вычитание, умножение, деление, сравнение символических и несимволических величин, оценку количества, определение последовательности чисел и подсчет.Правильные ответы суммировались и преобразовывались в процентильный ранг на основе возрастных норм по трем субшкалам: умение считать, счет и общие математические способности.
Руки и интеллект оценивались индивидуально на одном сеансе в небольшой детской лаборатории. Математические способности оценивались в виде группового теста (максимум 15 детей) на отдельном занятии в большом зале для семинаров. В каждом образце эти данные были получены максимум тремя разными научными сотрудниками, которые были заранее тщательно ознакомлены с процедурой тестирования.Перед сбором данных каждый ассистент прошел три контролируемых практических занятия с детьми, не участвовавшими в текущем исследовании.
Математические способности оценивались в виде группового теста (максимум 15 детей) на отдельном занятии в большом зале для семинаров. В каждом образце эти данные были получены максимум тремя разными научными сотрудниками, которые были заранее тщательно ознакомлены с процедурой тестирования.Перед сбором данных каждый ассистент прошел три контролируемых практических занятия с детьми, не участвовавшими в текущем исследовании.
Анализ ассоциации генов и мозга
Многолокусная модель, основанная на ядерных машинах наименьших квадратов, была объединена с консервативным статистическим выводом по вокселям, основанным на теории случайных полей, для проверки совместных нелинейных ассоциаций между 18 SNP и многомерными паттернами в объемных изображениях серого вещества при удалении линейного эффекта ковариаты возраста, пола, руки и общего внутричерепного объема [15].Полученные R 2 статистические изображения были проверены на значимость с использованием процедуры перестановки (выполнение 10 000 перестановок) на основе параметрической хвостовой аппроксимации и впоследствии преобразованы в P -значных изображений [15].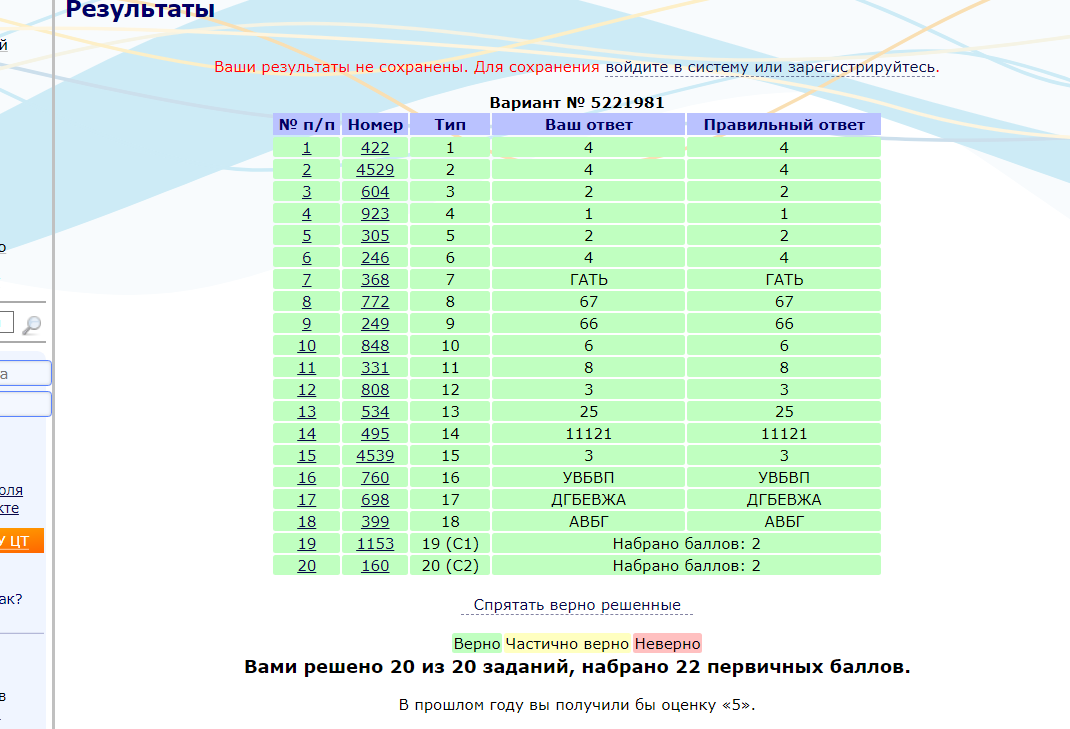 Ассоциации считались значимыми, когда кластеры оставались ниже произвольно определенного порога высоты P <0,05 (с поправкой на семейную ошибку для количества тестируемых вокселов и генов) и превышали произвольный порог протяженности k> 100 вокселей.Во время семейной коррекции ошибок статистический порог каждого вокселя был скорректирован путем (1) умножения его на общее количество протестированных 408 965 вокселей с учетом эффективной гладкости сигналов, а затем (2) умножения полученного порог каждого вокселя с общим количеством 10 протестированных генов. Эти анализы проводились в Matlab (https://www.mathworks.com) и SPM 12.
Ассоциации считались значимыми, когда кластеры оставались ниже произвольно определенного порога высоты P <0,05 (с поправкой на семейную ошибку для количества тестируемых вокселов и генов) и превышали произвольный порог протяженности k> 100 вокселей.Во время семейной коррекции ошибок статистический порог каждого вокселя был скорректирован путем (1) умножения его на общее количество протестированных 408 965 вокселей с учетом эффективной гладкости сигналов, а затем (2) умножения полученного порог каждого вокселя с общим количеством 10 протестированных генов. Эти анализы проводились в Matlab (https://www.mathworks.com) и SPM 12.
проводился с использованием набора инструментов G*Power (http://www.gpower.hhu.де). Достигнутая мощность была рассчитана апостериорно с использованием статистической основы критерия согласия, основанного на наблюдении, что примененная нами многомерная модель дает приблизительную статистику теста χ 2 , которую можно аналогичным образом преобразовать в коэффициент корреляции и p . -значение [15]. Входными параметрами этого расчета мощности были размер эффекта Коэна при = 0,47, вероятность альфа-ошибки 0,05 и размер выборки n = 101.Размер выборки, необходимый для воспроизведения этого эффекта с мощностью 0,8, был рассчитан априори также в рамках теста согласия χ 2 с использованием размера эффекта Коэна w = 0,47, вероятности альфа-ошибки 0,05, и уровень мощности 0,8 в качестве входных параметров.
-значение [15]. Входными параметрами этого расчета мощности были размер эффекта Коэна при = 0,47, вероятность альфа-ошибки 0,05 и размер выборки n = 101.Размер выборки, необходимый для воспроизведения этого эффекта с мощностью 0,8, был рассчитан априори также в рамках теста согласия χ 2 с использованием размера эффекта Коэна w = 0,47, вероятности альфа-ошибки 0,05, и уровень мощности 0,8 в качестве входных параметров.
Анализ ассоциации мозг-поведение
Для выявления вокселов, которые были в значительной степени связаны с результатами математических тестов, в кластерах, полученных в результате анализа генетической ассоциации, использовался подход многомерного анализа паттернов на основе прожектора.С этой целью для каждого воксела в этих кластерах мы определили сферическую окружающую область размером 4 мм (прожектор) и выполнили регрессионный анализ опорного вектора для каждой возможной позиции прожектора в рамках 10-кратной схемы перекрестной проверки. Коэффициенты детерминации ( R 2 ) были назначены каждому вокселу в его центре и непараметрически оценены на значимость путем запуска 10 000 перестановок обучающих и тестовых данных, чтобы получить нулевое распределение по вокселам.Во время коррекции теста перестановки для ложных срабатываний наблюдаемые результаты были случайным образом передискретизированы 10 000 раз, чтобы построить эмпирическую оценку нулевого распределения, из которой можно получить статистику теста (коэффициент детерминации). Воксели идентифицировали как значимые путем подсчета количества раз, когда статистика теста была меньше или больше, чем статистическое значение, полученное из наборов переставленных данных, и умножения этого значения на минимальное P -значение теста перестановки (1/(n+ 1), n = 10 000).Влияние ковариат, не представляющих интереса, включая возраст, пол, рукопожатие, общий внутричерепной объем, уровень образования матери и невербальный IQ, были удалены на основе перекрестно проверенного метода смешанной регрессии [30].
Коэффициенты детерминации ( R 2 ) были назначены каждому вокселу в его центре и непараметрически оценены на значимость путем запуска 10 000 перестановок обучающих и тестовых данных, чтобы получить нулевое распределение по вокселам.Во время коррекции теста перестановки для ложных срабатываний наблюдаемые результаты были случайным образом передискретизированы 10 000 раз, чтобы построить эмпирическую оценку нулевого распределения, из которой можно получить статистику теста (коэффициент детерминации). Воксели идентифицировали как значимые путем подсчета количества раз, когда статистика теста была меньше или больше, чем статистическое значение, полученное из наборов переставленных данных, и умножения этого значения на минимальное P -значение теста перестановки (1/(n+ 1), n = 10 000).Влияние ковариат, не представляющих интереса, включая возраст, пол, рукопожатие, общий внутричерепной объем, уровень образования матери и невербальный IQ, были удалены на основе перекрестно проверенного метода смешанной регрессии [30]. Анализы проводились с использованием The Decoding Toolbox (https://sites.google.com/site/tdtdecodingtoolbox/) и Matlab. Коэффициенты определения отдельных анализов ассоциаций мозга и поведения для навыков счета и счета сравнивались с помощью z-тестов Менга.
Анализы проводились с использованием The Decoding Toolbox (https://sites.google.com/site/tdtdecodingtoolbox/) и Matlab. Коэффициенты определения отдельных анализов ассоциаций мозга и поведения для навыков счета и счета сравнивались с помощью z-тестов Менга.
Благодарности
Членами консорциума Legascreen являются: Майкл А.Skeide 1 , INDRA KRAFT 1 , GESA Schaadt 1 , Николь Neef 1 , Jens Brauer 1 , Liane Dörr 1 , Ivonne Czepezauer 2 , Bent Müller 2 , Arndt Wilcke 2 , Хольгер Кирстен 2,3,4 , Йоханнес Больтце 5 , Франк Эммрих 2 и Анджела Д. Фридеричи 1 .
1 Кафедра нейропсихологии, Институт когнитивных исследований человека и мозга им. Макса Планка, Лейпциг, Германия,
2 Отделение когнитивной генетики, Институт клеточной терапии и иммунологии им. Фраунгофера, Лейпциг, Германия,
3 Институт медицинской информатики, статистики и эпидемиологии Лейпцигского университета, Лейпциг, Германия,
4 Лейпцигский исследовательский центр болезней цивилизации, Лейпцигский университет, Лейпциг, Германия,
5 Школа естественных наук Уорикского университета, Ковентри, Соединенное Королевство
Каталожные номера
- 1.
 Rimfeld K. et al. Стабильность учебных достижений в школьные годы во многом объясняется генетическими факторами. Наука обучения 16 (2018).
Rimfeld K. et al. Стабильность учебных достижений в школьные годы во многом объясняется генетическими факторами. Наука обучения 16 (2018). - 2. Docherty S. J. et al., Полногеномное ассоциативное исследование выявляет несколько локусов, связанных с математическими способностями и инвалидностью. Genes Brain Behav 9, 234–247 (2010). пмид:20039944
- 3. Барон-Коэн С. и др., Полногеномное исследование ассоциации математических способностей выявило ассоциацию на хромосоме 3q29, локусе, связанном с аутизмом и трудностями в обучении: предварительное исследование. PLoS ONE 9, e96374. (2014). пмид:24801482
- 4. Mascheretti S. et al., KIAA0319 и ROBO1 : доказательства связи с чтением и плейотропными эффектами на языковые и математические способности при дислексии развития. J Hum Genet 59, 189–197 (2014). пмид:24430574
- 5.
Chen H. et al., Полногеномное ассоциативное исследование выявляет генетические варианты, связанные со способностями к математике.
 Научный представитель 7, 40365 (2017).пмид:28155865
Научный представитель 7, 40365 (2017).пмид:28155865 - 6. Улен М. и др., Протеомика. Тканевая карта протеома человека. Наука 347, 1260419 (2015). пмид:25613900
- 7. Менон В., «Арифметика в мозгу ребенка и взрослого» в Оксфордском справочнике по математическому познанию, Коэн Кадош Р., Даукер А., ред. (Издательство Оксфордского университета, Оксфорд, 2015 г.).
- 8. Нидер А. Нейронный код числа. Nat Rev Neurosci 17, 366–382 (2016). пмид:27150407
- 9.Баттерворт Б., Уолш В. Нейронные основы математического познания. Curr Biol 21, R618–621 (2011). пмид:21854998
- 10. Ансари Д., Влияние развития и инкультурации на представление чисел в мозгу. Nat Rev Neurosci 9, 278–291 (2008). пмид:18334999
- 11.
Qin S. et al., Гиппокампально-неокортальная функциональная реорганизация лежит в основе когнитивного развития детей. Nat Neurosci 17, 1263–1269 (2014).
 пмид:25129076
пмид:25129076 - 12. Сакураи Т., Роль NRCAM в развитии нервной системы и нарушениях — помимо простого клея в мозгу. Mol Cell Neurosci 49, 351–363 (2012). пмид:22182708
- 13. Gonda Y. et al., ROBO1 регулирует миграцию и ламинарное распределение пирамидных нейронов верхнего слоя коры головного мозга. Кора головного мозга 23, 1495–1508 (2013). пмид:22661412
- 14. Курше Дж.et al., Терминальное ветвление аксона регулируется киназным путем LKB1 — NUAK1 посредством пресинаптического захвата митохондрий. Cell 153, 1510–1525 (2013). пмид:237
- 15. Ге Т., Фэн Дж. Ф., Хибар Д. П., Томпсон П. М., Николс Т. Э., Повышение мощности исследований ассоциаций по всему геному по вокселям: теория случайных полей, машины наименьших квадратов ядра и быстрые процедуры перестановки. Нейроизображение 63, 858–873 (2012). пмид:22800732
- 16.
 Hernandez-Miranda L.R. et al., ROBO1 регулирует передачу сигналов семафорина, чтобы направлять миграцию корковых интернейронов через вентральную часть переднего мозга. J Neurosci 31, 6174–6187 (2011). пмид:21508241
Hernandez-Miranda L.R. et al., ROBO1 регулирует передачу сигналов семафорина, чтобы направлять миграцию корковых интернейронов через вентральную часть переднего мозга. J Neurosci 31, 6174–6187 (2011). пмид:21508241 - 17.
Andrews W. et al., ROBO1 регулирует развитие основных путей аксонов и миграцию интернейронов в переднем мозге. Разработка 133, 2243–2252 (2006). пмид:166
- 18. Yeh M.L. и соавт., ROBO1 модулирует пролиферацию и нейрогенез в развивающемся неокортексе. J Neurosci 34, 5717–5731 (2014). пмид:24741061
- 19. Кантлон Дж. Ф., Браннон Э. М., Картер Э. Дж., Пелфри К. А., Функциональная визуализация числовой обработки у взрослых и 4-летних детей. PLoS Biol 4, e125 (2006). пмид:16594732
- 20.
Амальрик М., Дехэн С., Происхождение мозговых сетей для продвинутой математики у опытных математиков. Proc Natl Acad Sci U S A 113, 4909–4917 (2016).
 пмид:27071124
пмид:27071124 - 21. Старр А., Либертус М.Е., Брэннон Э.М., Чувство числа в младенчестве предсказывает математические способности в детстве. Proc Natl Acad Sci USA 110, 18116–18120 (2013). пмид:24145427
- 22. Арсалиду М., Тейлор М. Дж., 2+2 = 4? Метаанализ областей мозга, необходимых для чисел и вычислений. Neuroimage 54, 2382–2393 (2011). пмид:20946958
- 23.Чон Х. А., Фридеричи А. Д., Что значит «быть экспертом» для мозга? Функциональная специфика и связность в экспертизе. Кора головного мозга 27, 5603–5615 (2017). пмид:27797834
- 24. Арсалиду М., Павлив-Левац М., Садеги М., Паскуаль-Леоне Дж. Области мозга, связанные с числами и вычислениями у детей: метаанализ исследований фМРТ. Dev Cogn Neurosci 30, 239–250 (2018). пмид:28844728
- 25.
Куинке Д., Киттлер Р., Кайзер М., Стоункинг М., Насидзе И., Оценка слюны как источника ДНК человека для популяционных и ассоциативных исследований.
 Anal Biochem 353, 272–277 (2006). пмид:16620753
Anal Biochem 353, 272–277 (2006). пмид:16620753 - 26. Граффельман Дж., Изучение диаллельных генетических маркеров: пакет HardyWeinberg. J Stat Software 64, 1–23 (2015).
- 27. Genomes Project C. et al., Глобальный справочник по генетической изменчивости человека. Природа 526, 68–74 (2015). пмид:26432245
- 28.Аульченко Ю. С., Рипке С., Айзекс А., ван Дуйн С. М., GenABEL: R-библиотека для полногеномного анализа ассоциаций. Биоинформатика 23, 1294–1296 (2007). пмид:17384015
- 29. Marques J.P. et al., MP2RAGE, последовательность с самокоррекцией поля смещения для улучшенной сегментации и T1-картирования в сильном поле. Neuroimage 49, 1271–1281 (2010). пмид:19819338
- 30. Снук Л., Милетик С., Шолте Х.С., Как контролировать путаницу при анализе декодирования данных нейровизуализации. Neuroimage 184, 741–760 (2019). пмид:30268846
Сколько вариантов может быть в A/B/n тесте?
Как только вы начинаете думать, что A/B-тестирование довольно просто, вы сталкиваетесь с новым стратегическим противоречием.
Это поляризует: сколько вариантов вы должны протестировать в сравнении с контролем?
Есть много разных мнений по этому поводу, некоторые из них совершенно противоположные. Часть из них сводится к стратегии, часть к математике.Некоторые из них могут зависеть от того, на каком этапе бизнеса вы находитесь, от сложности вашей программы.
Как бы то ни было, это не совсем простой и простой ответ. Начнем с простого: с математики.
Проблема множественных сравнений
Когда вы одновременно тестируете множество вариантов, вы сталкиваетесь с так называемой «кумулятивной альфа-ошибкой».
По сути, чем больше вариантов теста вы запускаете, тем выше вероятность ложных срабатываний.
Скажем так: если вы действуете на основе принятия решений со значимостью 95 %, вероятность ошибки 1-го типа («альфа-ошибка» или ложное срабатывание) составляет 5 %.Это означает, что в 5% всех случаев делается предположение о значительном эффекте, хотя на самом деле его нет вообще. k
k
Альфа = выбранный уровень значимости, как правило 0.05
k = количество вариантов теста в вашем тесте (без контроля)
Таким образом, вы можете видеть, что риск ложного срабатывания резко возрастает с каждым новым вариантом. Тогда должно быть очевидно — протестируйте только один вариант, верно?
Ну, не совсем. Большинство инструментов, включая Optimizely, VWO и Conductrics, имеют встроенные процедуры для исправления так называемой проблемы множественных сравнений. Они могут использовать разные методы, но они решают проблему.
И даже если ваш инструмент тестирования не имеет встроенной процедуры исправления, вы все равно можете исправить альфа-ошибку самостоятельно.Существует множество различных методов, и я не являюсь экспертом по компромиссам между ними (может быть, настоящий статистик сможет вмешаться):
Несмотря на то, что корректируя альфа-ошибку, вы снижаете риск ошибок типа I, но увеличиваете риск ошибок типа II (не видя разницы, когда она на самом деле есть).
Кроме того, Эндрю Гельман написал замечательную статью, в которой утверждается, что проблема множественных сравнений может полностью исчезнуть, если рассматривать ее с иерархической байесовской точки зрения.
Идан Михаэли, главный специалист по данным в Dynamic Yield, также отмечает, что использование байесовского подхода решает эту проблему:
Идан Михаэли:
«Проблема множественного сравнения действительно является серьезной проблемой при A/B-тестировании множества вариантов и/или нескольких целей (KPI). Однако в основном это недостаток стандартного широко используемого подхода к A/B-тестированию, который называется тестированием гипотез. Один из способов решить эту проблему — использовать байесовский подход к A/B-тестированию, как описано в моей недавней статье о байесовском тестировании.
Как выразился Мэтт Гершофф, генеральный директор Conductrics, это предполагает, что у вас есть сильное априорное предположение, что вариации действительно одинаковы — все это действительно приводит к частичному объединению данных, о чем Мэтт написал в этом замечательном посте.
Если вы все еще боитесь математических последствий сравнения нескольких средних, обратите внимание, что вы действительно делаете то же самое, когда выполняете сегментацию данных после тестирования. Крис Стуккио из VWO написал об этом отличную статью:
.Крис Стуккио:
«У вас есть мобильные и настольные компьютеры, 50 штатов и, возможно, 20 важных источников реферального трафика (поиск Google, партнерские ссылки и т. д.).В общем, это 2 х 50 х 20 = 2000 сегментов. Теперь давайте предположим, что каждый сегмент идентичен любому другому сегменту; если вы сегментируете свои данные, вы получите 0,05 x 2000 = 100 статистически значимых результатов чисто случайно.
К счастью, пользователи Android в Кентукки по рекомендации Google, пользователи iPhone в Небраске по рекомендации Direct и пользователи ПК в Нью-Джерси предпочли новый дизайн. Ух ты!»
В заключение, если вы работаете с правильным инструментом или у вас есть достойные аналитики, математика на самом деле не проблема. Математика сложная, но не невозможная и не опасная. Как метко выразился Мэтт Гершофф, «главное — не слишком зацикливаться на подходе [исправления], а просто в том, чтобы это было сделано».
Математика сложная, но не невозможная и не опасная. Как метко выразился Мэтт Гершофф, «главное — не слишком зацикливаться на подходе [исправления], а просто в том, чтобы это было сделано».
Также спасибо Мэтту за то, что он помог мне разобраться со всей математикой.
Итак, не принимая во внимание математический аспект, нам остается принять стратегическое решение. Где ROI, тестировать как можно больше вариантов или ограничивать объем и, возможно, быстрее переходить к следующему тесту?
Обоснование максимизации числа вариантов
Google протестировал 41 оттенок синего.Некоторым это нравится, а некоторые ненавидят такие решения.
Image SourceХотя у большинства людей нет такого трафика, суть остается неизменной: это принятие решений на основе данных. Без мнения, без стиля.
Теперь, учитывая реалии трафика (вы не можете тестировать, как это делает Google), подходит ли вам стиль тестирования множества вариантов одновременно? Некоторые так говорят.
Эндрю Андерсон, директор по оптимизации Recovery Brands, недавно написал пост, в котором изложил свою методологию тестирования на основе дисциплины.В этом посте он написал:
Эндрю Андерсон:
«Чем меньше вариантов, тем менее ценен тест. Что-либо с менее чем четырьмя вариантами, насколько я понимаю, не годится для нашей программы из-за ограниченных шансов открытия, успеха и, что наиболее важно, масштаба результата. Я буду отдавать приоритет тестам с 10 вариантами, а не тестам с пятью, даже если я думаю, что изменение для пяти, скорее всего, будет более эффективным. Самое главное – это ассортимент и количество вариантов.
Эти правила не являются специфическими для теста, поэтому я предлагаю следовать этому курсу оптимизации только для сайтов, у которых есть не менее 500 конверсий в месяц, а минимум 1000 в месяц более разумен. Независимо от максимального количества ресурсов, бета-концепций и трафика, которым вы можете управлять, это и есть цель.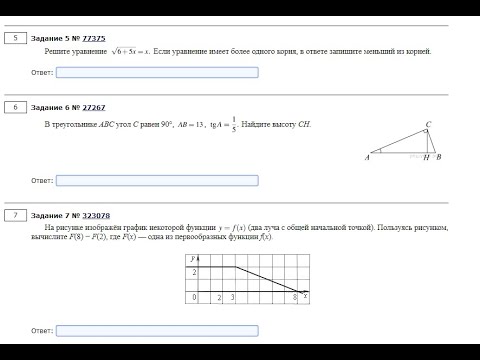 Вот почему Марисса Майер и Google, как известно, провели тест на 40 оттенков синего, они смогли».
Вот почему Марисса Майер и Google, как известно, провели тест на 40 оттенков синего, они смогли».
Этот подход резко отличается от того, что советуют многие эксперты. Мало того, что многие люди советуют вам тестировать только один элемент за раз (плохой совет), большинство людей говорят, что вы должны придерживаться простого теста A vs B.
Естественно, я обратился к Эндрю за разъяснениями. В конце концов, его подход, кажется, работает и для более крупных компаний, таких как Microsoft, Amazon и, конечно же, Google. Это работает и для компаний с меньшим трафиком? Насколько применим подход?
Вот что он сказал:
Эндрю Андерсон:
«Я беру столько, сколько позволяют трафик и ресурсы. Это часть изучения сайта из первых нескольких тестов, которые я делаю (здесь также помогает исследование дисперсии).Самый важный ключ, который нужно помнить, заключается в том, что чем больше изменение, тем больше я, вероятно, смогу протестировать (или, по крайней мере, рисками становится легче управлять).
Максимальное количество вариантов, которые я когда-либо делал в одном тесте, обычно составляет около 14-15. Я пытаюсь смоделировать хрупкость, чтобы выяснить, в чем заключается наилучшая точка. Даже на сайтах с самым высоким трафиком (а я работал на 16 из 200 лучших сайтов) оптимальная точка обычно находится в диапазоне 12-16. Я никогда не тестирую менее чем с 4 вариантами. Также имейте в виду бета вариантов важнее, чем количество вариантов .Вот почему я заставляю свою команду думать с точки зрения концепций и воплощений концепций, чтобы мы не слишком сузили фокус.
С моими текущими настройками у нас есть большое количество сайтов, поэтому мы группируем сайты по количеству возможностей, которые мы можем разумно протестировать. Наши самые крупные сайты, которые все еще находятся в низком среднем диапазоне, получают 7-8 альтернатив. Самые низкие сайты (около 10 конверсий в день), которые мы тестируем, получают 4-5. Сайты, которые никогда не станут управляемыми ниже этой отметки, мы не тестируем и ищем другие способы оптимизации.
Какой смысл? Эффективность. Вы тестируете это множество вариантов и ограничиваете мнения, которые сдерживают программу тестирования. Это также (на мой взгляд, это не мысли Эндрю) похоже на то, как The Onion заставляет писателей придумывать по 20 заголовков на статью. Первые несколько простых, но к последним 5 вы действительно раздвигаете границы и отбрасываете предположения. Протестируйте много дерьма, и вы обязательно получите некоторые решения, о которых иначе бы и не подумали.
Эндрю, конечно, не единственный, кто выступает за тестирование нескольких вариантов.Идан Михаэли из Dynamic Yield сказал, что трудно установить ограничение на количество тестируемых вариантов. Он также упомянул, что разница между вариантами является решающим фактором, независимо от того, сколько вариантов вы используете.
«Чем существеннее разница во внешнем виде, тем быстрее вы сможете обнаружить разницу в производительности статистически значимым образом», сказал он
Однако чаще всего число вариантов соответствует типу ответа «в зависимости от обстоятельств».Отдельные факторы, с которыми вы имеете дело, имеют гораздо большее значение, чем заложенная в камне стратегия.
Обоснование минимизации количества вариаций
Многие люди выступают за то, чтобы тестировать меньше вариантов, а не много. Некоторые по математическим причинам, которые мы обсуждали выше, некоторые как средство стратегии оптимизации.
Одно замечание: с корректировками альфа почти всегда требуется больше времени для запуска теста с большим количеством вариантов. Вы можете использовать строго итеративный подход, когда вы изучаете поведение пользователей на детальном уровне и тестируете только один или несколько вариантов за раз.Или, возможно, ваша организация давно не проводила тестирование, и вы хотите продемонстрировать несколько быстрых побед, не вдаваясь в мельчайшие детали ANOVA и взвешивания альфа-ошибок.
Итак, вы можете протестировать добавление ценностного предложения против вашего текущего (отсутствующего) ценностного предложения. Вы получаете быструю победу и можете перейти к увеличению скорости тестирования, эффективности и поддержки программы.
Есть и другие причины, которые упоминались в пользу сокращения количества вариаций.
Образец загрязнения
Также возникает вопрос о загрязнении образца, который возникает, когда образец не является действительно рандомизированным или когда пользователи подвергаются множеству вариаций в тесте.
Вот как выразился Тон Весселинг, основатель Online Dialogue:
Тон Весселинг:
«Когда пользователи вернутся к эксперименту, некоторые из них удалят свои файлы cookie, некоторые (чаще многие!) будут использовать другое устройство.
С 1 вариацией происходит изменение на 50%, они в конечном итоге остаются в той же вариации, если возвращаются в эксперимент.Если у вас есть 3 вариации, разница составляет всего 25%, и они окажутся в одной и той же вариации.
Чем больше вариаций, тем больше загрязнение.
Загрязненные образцы приведут к тому, что коэффициенты пересчета для каждой вариации будут ближе друг к другу (при длительном эксперименте образцы будут настолько загрязнены, что станут почти идентичными — поэтому коэффициент пересчета одинаков для всех вариантов)».
Если вы хотите узнать больше о загрязнении образцов при A/B-тестировании, прочитайте нашу статью об этом.
Трафик и время
Время и трафик тоже имеют значение. Сколько времени нужно, чтобы создать 10 совершенно разных вариаций вместо одной? Сколько трафика у вас есть и сколько времени вам понадобится, чтобы провести действительный тест?
Вот как Тон выразился:
Тон Весселинг:
«Кроме того, только один вариант, потому что на большинстве веб-сайтов недостаточно пользователей и конверсий для проведения экспериментов с несколькими вариантами — поэтому, пожалуйста, всегда говорите людям начинать с одного (а эксперименты — это культура быстрого обучения, поэтому, пожалуйста, даже если вы можете идентифицировать пользователей на основе входа в систему, не запускайте тесты, которые занимают так много времени, что все о них забывают…)
Загрязнение образцов означает, что с большим количеством вариантов вам потребуется больше посетителей и конверсий, чтобы доказать победителя.Но, как я уже говорил, вы не хотите растягивать время выполнения теста (потому что: большее загрязнение, а также потребление пропускной способности для экспериментов).
Не рассчитывая на время, вам нужно создавать варианты с более смелыми изменениями (потенциально большее влияние), но это требует гораздо больше времени и ресурсов, поэтому имеет смысл провести эксперимент только с одним смелым вариантом.
Вы хотите продолжать использовать всю пропускную способность эксперимента, проводя как можно больше экспериментов.Лучше провести 10 экспериментов A/B в нескольких местах вашего сайта, чем один большой эксперимент в одном месте — вы получите больше информации о поведении».
Тон также упомянул, что запуск только одного варианта против контроля — это хороший способ исследовать мотивы покупателей/пользователей — в основном, чтобы изучить, что работает, а что нет — а затем использовать это с помощью других средств, таких как бандиты:
Тон Весселинг:
«Если мы знаем, как и где мы можем мотивировать этих пользователей, мы чаще переходим к Эксплуатации и запускаем там Бандитские эксперименты с несколькими вариациями на основе этих конкретных знаний (и если у вас есть трафик, сегментированный и/или контекстный быть в пути).Но это все о зарабатывании денег, а не об обучении, но мы хороши на этом этапе эксплуатации, потому что мы узнали заранее благодаря нашему подходу к исследованию».
Есть золотая середина, тоже
Я спросил доктора Джулию Энгельманн, руководителя отдела данных и аналитики в Web Arts/konversionsKRAFT, как они решают, сколько вариантов тестировать, и она сказала, что на самом деле нет единого ответа, подходящего для всех.
Как она выразилась: «Я не думаю, что можно дать общий ответ.Конкретная установка теста зависит от ряда факторов (см. ниже). По моему личному опыту и мнению, я бы никогда не тестировал более пяти вариантов (включая контроль) одновременно.
Идан Михаэли тоже считает, что это зависит от множества факторов и однозначного ответа не существует:
Идан Михаэли:
«Все зависит от того, насколько вы смелы и как быстро хотите получить результаты. Ваши ресурсы — это ваш трафик и ваше творчество, и вы должны использовать их с умом.Компромисс между исследованием и эксплуатацией означает, что вам нужно сбалансировать свое желание использовать имеющиеся у вас знания, предоставляя пользователям наилучший опыт, который вы когда-либо знали, и в то же время рискуя предоставить неоптимальный опыт, когда вы пытаетесь найти еще лучший опыт.
Здесь нет серебряной пули. Делайте все возможное, чтобы придумать разнообразный набор вариантов и рискните исследовать их в краткосрочной перспективе, чтобы улучшить производительность в долгосрочной перспективе. Не создавайте новый вариант только для того, чтобы протестировать больше — делайте это только в том случае, если у вас есть разумное убеждение, что он будет лучше, чем все, что вы пробовали до сих пор.
Если исходить из того, что нет однозначного ответа, как вы решаете, сколько вариантов тестировать? Даже если вы верите в максимизацию вариаций, как вы решаете, какое их количество является оптимальным?
Какие факторы определяют, сколько вариантов вы ставите против контроля?
Возможно, было бы неразумно советовать разнообразной аудитории, читающей это, либо протестировать 41 оттенок цвета, либо просто придерживаться одного варианта. Точно так же, как ваши аудитории, конверсии, доход, трафик и т.отличаются, как и структура вашей компании, политика и процессы. Однозначный ответ на все вопросы на самом деле невозможен.
Тем не менее, есть некоторые факторы, которые помогут вам выбрать точный подход.
По словам Тона, при определении плана эксперимента вы смотрите на обычные факторы:
Тон Весселинг:
«Пользователи/конверсии и экспериментальная пропускная способность, процент выигрышей и ресурсы. Но это больше касается того, сколько экспериментов вы будете проводить за период времени.Потому что все должно быть с 1 вариацией :-)”
Доктор Джулия Энгельманн дает свои критерии, в основном с точки зрения статистики:
Доктор Юлия Энгельманн:
- Транспорт. Если это веб-сайт с низким трафиком, я обычно рекомендую тестировать с меньшим количеством вариантов, но с высокой контрастностью.
- Контраст вариантов по сравнению с контролем . Чем выше расчетный подъем вариации, тем больше вероятность, что вы обнаружите этот подъем с помощью тестирования.
- Предполагаемая продолжительность тестирования , которая является приемлемой и соответствует бизнес-целям
- Приемлемый коэффициент альфа-ошибки – каков максимальный уровень риска, на который вы готовы пойти? Чем больше количество вариантов, тем выше вероятность ошибочного принятия решения. Если вы тестируете очень большую концепцию, которая может иметь огромное влияние на бизнес, но также требует больших затрат ресурсов, имеет смысл быть очень уверенным в результате теста.Таким образом, я бы рекомендовал высокий уровень достоверности и меньше тестовых вариантов».
И, как цитировалось Эндрю ранее в статье, он использует модели уязвимости, чтобы найти золотую середину в заданном контексте. По его словам, «даже на сайтах с самым высоким трафиком (а я работал с 16 из 200 лучших сайтов) оптимальная точка обычно находится в диапазоне 12–16».
Что касается поиска областей возможностей и элементов воздействия, Эндрю написал, что у него есть ряд различных типов тестов, предназначенных для максимального обучения, таких как MVT, проверка существования и персонализация.Когда он концентрируется на областях воздействия, он пытается максимизировать бета-варианты и для данного решения также пытается протестировать противоположное этому (о чем будет написано в следующей статье).
Аккаунт для ваших ресурсов
Помимо трафика, вы должны учитывать свои индивидуальные ресурсы и организационную эффективность. Сколько времени требуется вашим командам дизайнеров и разработчиков для серии огромных изменений по сравнению с постепенным тестированием (стиль 41 оттенок синего)? Первых много, вторых почти нет.
Источник изображенияТон, во-первых, советует: «Пожалуйста, не делайте штуку с цветом кнопки, вы хотите узнать, что движет поведением и как вы можете мотивировать пользователей сделать следующий шаг. С другой стороны, с ресурсами для разработки интерфейса, такими как testing.agency, более смелые эксперименты не должны стоить миру — и нехватка ресурсов больше не может вас сдерживать».
В принципе, небольшие изменения (цвет кнопки) не требуют почти нулевых ресурсов, поэтому их легче протестировать во многих вариантах. Кроме того, из-за незначительных изменений, которые фундаментально не влияют на поведение пользователей, они вряд ли окажут большой эффект.
С другой стороны, радикальные изменения требуют больше ресурсов, но у вас больше шансов их увидеть и произвести. И когда вы сравниваете несколько радикальных изменений друг с другом, вы с большей вероятностью увидите оптимальный (или близкий к оптимальному) опыт.
Эндрю хорошо выразил это в своей статье CXL: «Если у меня есть 5 долларов, и я могу получить 10, отлично, но если я могу получить 50, или 100, или 1000, тогда мне нужно это знать, и это единственный способ, которым я могу сделать это через открытие и использование возможных альтернатив.
Заключение
Несмотря на то, что это большой облом для tl;dr, нет черно-белого ответа. И у меня нет лошади в этой гонке, я фанат той, которая показывает лучшие результаты. Это зависит от вашего трафика, конверсий, аудитории, корпоративной культуры и процессов.
Однако математика, вообще говоря, не является ограничивающим фактором. Причем выбирать следует исходя из перечисленных выше факторов. В пользу большего количества вариантов вы избегаете ограничений на идеи из-за того, что, по вашему мнению, будет (или не будет работать).Если разница между вариантами велика, вы гораздо более уверены в победе.
Ограничение вариаций связано с опасениями по поводу загрязнения образцов, трафика и времени/ресурсов.
Наконец, одна и та же организация может проводить оба типа тестов. Это стратегическое решение, которое я не обязательно могу принять за вас.
Источник изображения функции
Специальность по математике | Математика
Студенты, которые поступили в Johns Hopkins в текущем учебном году, должны обратиться к текущему Академическому каталогу для получения текущего списка основных требований.Студенты, поступившие в Университет Джонса Хопкинса в предыдущем учебном году, должны обратиться к каталогу этого учебного года.Основные требования
Перечисленные требования для получения степени бакалавра в области математики дополняют общие требования университета для специальностей факультетов. Курсы, используемые для удовлетворения требований, должны быть завершены с оценкой C- или выше.
Исчисление: Исчисление I, II и III. Майоры поощряются, но не обязаны выбирать варианты с отличием.
Линейная алгебра: 110.201 Линейная алгебра ИЛИ 110.212 Линейная алгебра с отличием
Анализ: 110,405 Реальный анализ I ИЛИ 110,415 Анализ с отличием I И один из
- 110.311 Комплексный анализ
- 110.406 Анализ II
- 110.407 Награждение Комплексный анализ
- 110.413 Введение в топологию
- 110.416 Анализ наград II
- 110.417 Частичные дифференциальные уравнения
- 110.421 Динамические системы
- 110.427 Введение в исчисление вариаций
- 110.439 Введение в дифференциальную геометрию
- 110.441 исчисление на многообразиях
- 110,443 Анализ Фурье
Алгебра: 110.401 Алгебра: 110.401 Расширенная алгебра I или 110.411
- 110.304 Введение в теорию чисел
- 110.412 Алгебра с отличием II
- 110.413 Введение в топологию
- 110.422 Теория представлений
- 110.423 Группы Ли для бакалавров
- 110.435 Введение в алгебраическую геометрию
(Примечание. Студенты могут использовать как 110.401, так и 110.411 для зачета, но только одна из них будет использоваться для основных требований.)
Факультативный: Еще один курс в 300 уровень или выше.
Требование вне курса: Два семестра в любой из следующих областей применения математики. (Примечание: другие подходящие, продвинутые, количественные курсы могут быть выбраны на этом или другом факультете с одобрения директора бакалавриата по математике.)
-
- физика: 171.204 Классическая механика, 171.301 Введение в электромагнитную теорию, 171.302 Темы в продвинутой электромагнитной теории, 171.303-4 Введение в квантовую механику, 171.312 Статистическая физика и термодинамика, 171.405 Конденсированная физика
- Химия: 030.345 Химические применения Теория групп, 030.453 Квантовая химия среднего уровня, 030.302 Физическая химия II
- Прикладная математика и статистика: 550.391 динамические системы, 550.420 Введение в вероятность, 550.426 Введение в стохастические процессы, 550.430 Введение в статистику, 550.453 Теория математической игры, 550.471 Комбинаторный анализ, 550.471 Гребная теория
- Экономика: 180.301 Микроэкономическая теория, 180.302 Макроэкономическая теория или 180.402 Расширенная микроэкономическая теория , 180.334 Эконометрика ИЛИ 180.434 Продвинутая эконометрика
- Философия: 150.420 Математическая логика I, 150.421 Математическая логика II, 150.422 Теория аксиоматических наборов
- Компьютера: 60539 Компьютеры и вычислительная теория, 601.464 Искусственный интеллект, 601.442 Современная криптография, 601.433 Введение в алгоритмы, 600.438 Вычислительная генамика, 601.488 Основы вычислительной биологии, 601.461 Компьютерное зрение, 601.457 Компьютерная графика, 601.475 6 Машинное обучение
Диплом с отличием
Почетные звания Департамента присуждаются всем обладателям степени бакалавра гуманитарных наук, которые также завершили следующие 6 курсов с общим минимальным средним баллом 3.6.
- 110.415-416 Анализ с отличием
- 110.411-412 Алгебра с отличием
- 110.407 Анализ с отличием Комплексный анализ ИЛИ 110.607 Комплексный анализ
- Еще один курс уровня 400 или выше
- Аналитика с отличием и Алгебра с отличием не зависят друг от друга и могут сдаваться в любом порядке или одновременно.
28 Advice: 3009028

 4.5a (p138)
4.5a (p138) 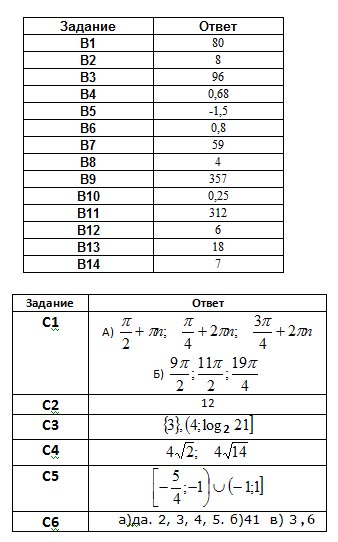
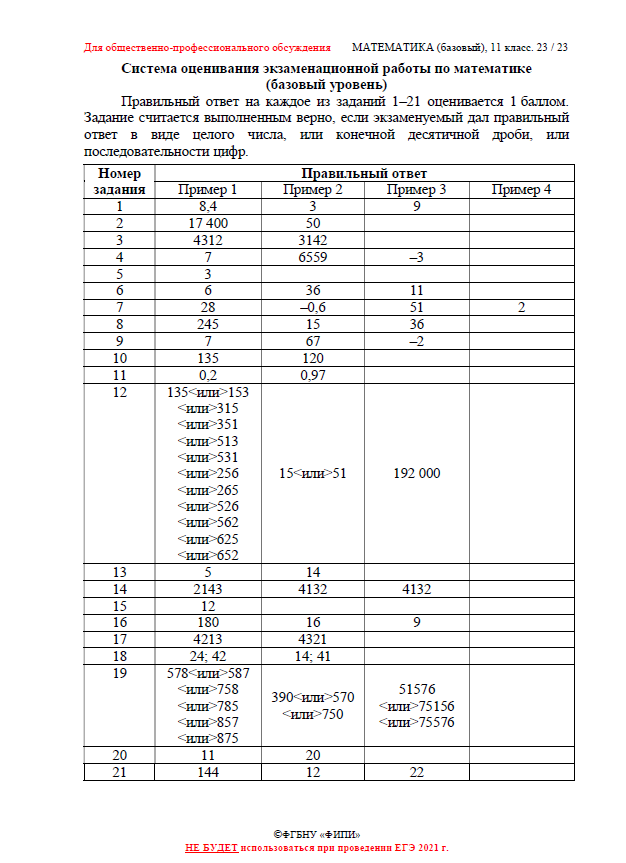
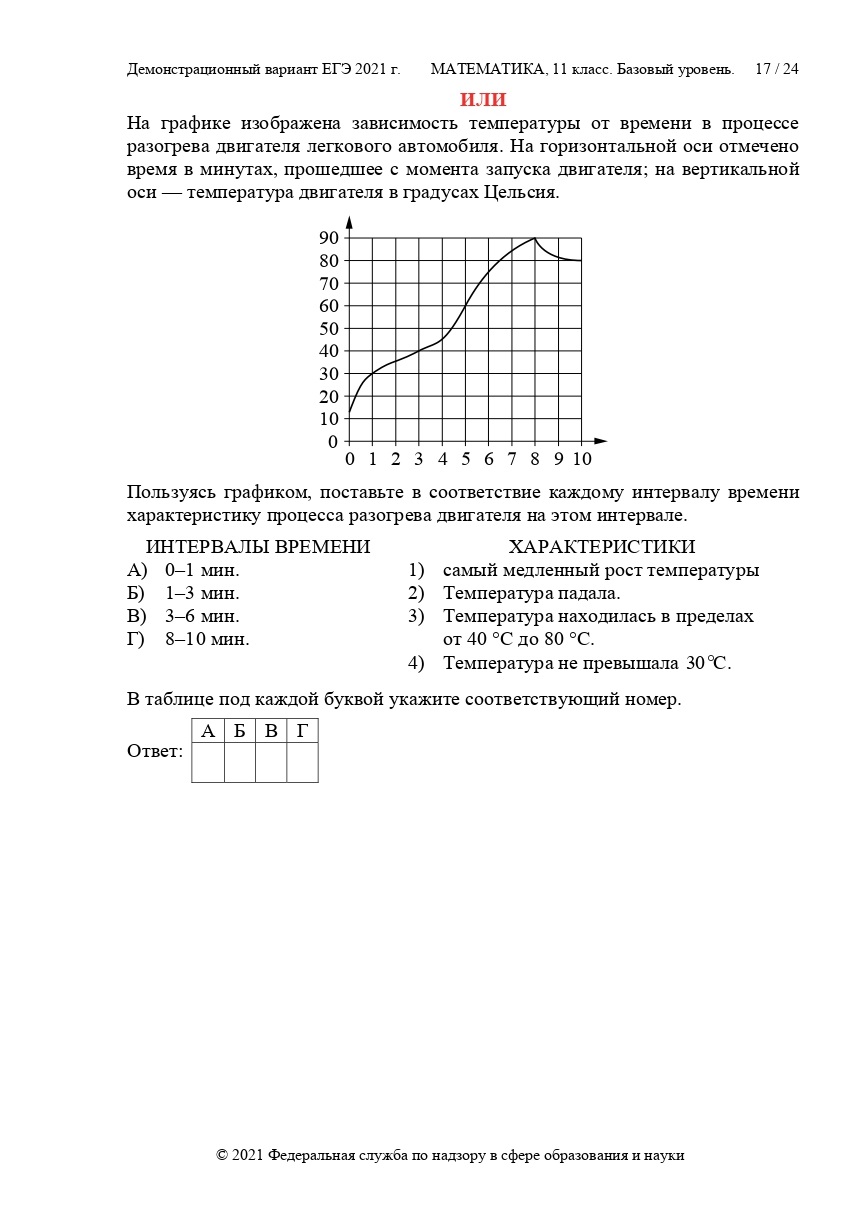
 7)
7)  2)
2)  2 кроме Объемов по срезам
2 кроме Объемов по срезам